E' possibile cliccare sulle intestazioni di ogni sezione per accedere alle tracce dei problemi.
NUMERI
Dalla sezione "I quattro 4, i cinque 5 e altri esercizi simili"
9. Esprimere un numero intero utilizzando quattro R


ARITMETICA E ALGEBRA
Dalla sezione "Le quattro operazioni e dintorni"
8. Vendo, compro, vendo

18.
 Vai alla sol.
Vai alla sol.Dalla sezione "Il problema della cisterna"
9.
 Vai alla sol.
Vai alla sol.Dalla sezione "Il problema di Flavius Josephus"
5. Un trucco con le carte

6.
 Vai alla sol.
Vai alla sol.7.
 Vai alla sol.
Vai alla sol.Dalla sezione "Divisioni di botti"
6.
 Vai alla sol.
Vai alla sol.Dalla sezione "Aritmetica russa"
1. Ordine delle cifre e divisibilità
 Vai alla disc.
Vai alla disc.2. Sostituire le coppie

3. Righe di 1000 numeri

5. Numeri buoni

6. Funzioni di funzioni

7. 3 automi giocano a carte

10.
 Vai alla sol.
Vai alla sol.Dalla sezione "Miscugli con travaso di liquidi"
3.
 Vai alla sol.
Vai alla sol.4.
 Vai alla sol.
Vai alla sol.Dalla sezione "Il gioco dei 4 numeri"
 Vai alla sol.
Vai alla sol.Dalla sezione "Ferri da cavallo"
Il re raduna un esercito

Il ferro da cavallo

Dalla sezione "La paga dei portatori"
Problemi sui quali ho dei dubbi

ANALISI
Dalla sezione "Il recinto degli ornitorinchi"
Il recinto degli ornitorinchi

GEOMETRIA SOLIDA
Dalla sezione "I due stiliti ed altre ricreazioni pitagoriche"
2. I serpenti attorno all'albero

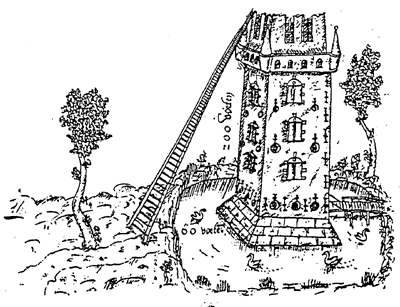
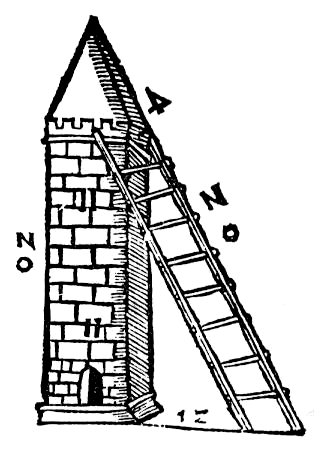
Dalla sezione "Le torri di Pitagora"
2.
 Vai alla sol.
Vai alla sol.3.
 Vai alla sol.
Vai alla sol.4. La canna appoggiata ad una parete

5.
 Vai alla sol.
Vai alla sol.6.
 Vai alla sol.
Vai alla sol.7.
 Vai alla sol.
Vai alla sol.Dalla sezione "Pitagora ed il fiore di loto"
1.
 Vai alla sol.
Vai alla sol.2.
 Vai alla sol.
Vai alla sol.Dalla sezione "Il bambù spezzato"
2.
 Vai alla sol.
Vai alla sol.3.
 Vai alla sol.
Vai alla sol.4.
 Vai alla sol.
Vai alla sol.Dalla sezione "I paradossi del tangram"
2. La casa
 Vai alla disc.
Vai alla disc.3.
 Vai alla sol.
Vai alla sol.4.
 Vai alla sol.
Vai alla sol.5.
 Vai alla sol.
Vai alla sol.6.
 Vai alla sol.
Vai alla sol.7.
 Vai alla sol.
Vai alla sol.8.
 Vai alla sol.
Vai alla sol.9.
 Vai alla sol.
Vai alla sol.10.
 Vai alla sol.
Vai alla sol.11.
 Vai alla sol.
Vai alla sol.12.
 Vai alla sol.
Vai alla sol.13.
 Vai alla sol.
Vai alla sol.14.
 Vai alla sol.
Vai alla sol.15.
 Vai alla sol.
Vai alla sol.16.
 Vai alla sol.
Vai alla sol.Dalla sezione "Gnomon"
3. Dividere un L-tromino in 5 parti uguali
 Vai alla disc.
Vai alla disc.Dalla sezione "Dissezioni del quadrato"
4. Dividere un quadrato in 7 quadrati uguali

5.
 Vai alla sol.
Vai alla sol.6.
 Vai alla sol.
Vai alla sol.Dalla sezione "Esercizi sulle dissezioni"
 Vai alla sol.
Vai alla sol. Vai alla sol.
Vai alla sol. Vai alla sol.
Vai alla sol.Dalla sezione "Il problema della mitra"
4. Due quadrati in una mitra

6.
 Vai alla sol.
Vai alla sol.Dalla sezione "Coprire un disco con altri dischi"
3. Il problema dei 7 dischi

Dalla sezione "Coprire un quadrato con altri quadrati"
Tappeti quadrati

Tappeti quadrati paralleli

Dalla sezione "Cerchi in un quadrato"
2. Cerchi in un triangolo equilatero

3. Cerchi in un cerchio

TOPOLOGIA
Dalla sezione "Visitare tutte le celle di una griglia"
7. Domande in cerca di risposta


8. Il nostro amico Dudeney


Dalla sezione "Il paradosso toroidale di Herbert Taylor"
Anello e manette bis


MISURE
Dalla sezione "Clessidre, orologi e calendari"
14.
 Vai alla sol.
Vai alla sol.Dalla sezione "L'arrampicata della lumaca"
4.
 Vai alla sol.
Vai alla sol.Dalla sezione "Pesi e bilance"
4. Le 9 palline e la bilancia romana
 Vai alla disc.
Vai alla disc.14. Nuovo interessante problema su: Pesi e bilance

LOGICA
Dalla sezione "Il putto autopoietico"
Il putto autopoietico
 Vai alla disc.
Vai alla disc.Dalla sezione "Paradossi"
1. Il paradosso del mentitore
 Vai alla disc.
Vai alla disc.2. Il paradosso del comma 22
 Vai alla disc.
Vai alla disc.3. Il paradosso di Parmenide
 Vai alla disc.
Vai alla disc.4. Il paradosso dell'autoriferimento
 Vai alla disc.
Vai alla disc.5. Il paradosso di Achille e della Tartaruga
 Vai alla disc.
Vai alla disc.6. Il paradosso del sorite
 Vai alla disc.
Vai alla disc.7. Il paradosso della decisione

8. Il paradosso della previsione
 Vai alla disc.
Vai alla disc.9. Il paradosso dell'infinito
 Vai alla disc.
Vai alla disc.10. Una delle due è falsa

11. Orrori

12. Come superare un esame

13. Come non farsi mangiare dai cannibali

14. Il paradosso del barbiere

15. Il paradosso del cartello (o del biglietto di Jourdain)

Dalla sezione "Il leopardo la capra ed il kassawi"
10.
 Vai alla sol.
Vai alla sol.12.
 Vai alla sol.
Vai alla sol.13.
 Vai alla sol.
Vai alla sol.14.
 Vai alla sol.
Vai alla sol.Dalla sezione "Logica e dintorni"
3.
 Vai alla sol.
Vai alla sol.COMBINATORIA
Dalla sezione "I labirinti logici di Robert Abbott"
Direzioni obbligate

Dalla sezione "I regoli di Golomb"
4. Sei punti su una circonferenza
 Vai alla sol.
Vai alla sol.Dalla sezione "Bianco e nero"
4. Il rovescio della medaglia

Dalla sezione "Esercizi sul principio dei cassetti"
7.
 Vai alla sol.
Vai alla sol.8.
 Vai alla sol.
Vai alla sol.9.
 Vai alla sol.
Vai alla sol.10.
 Vai alla sol.
Vai alla sol.11. Somma divisibile per n

12.
 Vai alla sol.
Vai alla sol.13.
 Vai alla sol.
Vai alla sol.14.
 Vai alla sol.
Vai alla sol.15.
 Vai alla sol.
Vai alla sol.16.
 Vai alla sol.
Vai alla sol.18. Alberi e distanze

19.
 Vai alla sol.
Vai alla sol.20.
 Vai alla sol.
Vai alla sol.21.
 Vai alla sol.
Vai alla sol.22.
 Vai alla sol.
Vai alla sol.23.
 Vai alla sol.
Vai alla sol.24.
 Vai alla sol.
Vai alla sol.25.
 Vai alla sol.
Vai alla sol.26.
 Vai alla sol.
Vai alla sol.27.
 Vai alla sol.
Vai alla sol.28.
 Vai alla sol.
Vai alla sol.29. Almeno un'aspirina al giorno

30.
 Vai alla sol.
Vai alla sol.31.
 Vai alla sol.
Vai alla sol.32.
 Vai alla sol.
Vai alla sol.Dalla sezione "I cassetti di Zio Erdos"
1. Cinque punti sul piano

2. Nove punti sul piano

3. Diciassette punti sul piano

4. il problema del lieto fine
 Vai alla disc.
Vai alla disc.PROBABILITA' E STATISTICA
Dalla sezione "Un triangolo forse"
2. Probabilità che sia un triangolo

3.
 Vai alla sol.
Vai alla sol.4. Perchè i professori (e le professoresse) disegnano sempre triangoli acutangoli?

Dalla sezione "Il paradosso di Bertrand"
Il paradosso di Bertrand

______________________
LEGENDA
 = dati insufficienti
= dati insufficienti = problema irrisolto
= problema irrisolto = problema risolto
= problema risolto = nuovo problema (2020)
= nuovo problema (2020) = problema aggiornato (2020)
= problema aggiornato (2020) = nuovo problema (2019)
= nuovo problema (2019) = problema aggiornato (2019)
= problema aggiornato (2019) = discussione aperta
= discussione aperta