Ok, Franco.
Supponiamo allora che la ditta assuma senza guardare la data del compleanno.
Siccome non conosco bene la teoria della probabilità, procederò per gradi.
---
1) Assume 1 persona.
In tal caso, per ogni giorno dell'anno la persona ha
$\displaystyle p(1)=\frac{364}{365}$
probabilità di lavorare.
I giorni lavorati da quella persona saranno
giorni lavorati per persona = $\displaystyle 365 \cdot \frac{364}{365}=364$
giorni totali = $\displaystyle1\cdot364=364$
---
2) Assume 2 persone.
In tal caso, per ogni giorno dell'anno entrambe le persone hanno
$\displaystyle p(2)=\left(\frac{364}{365}\right)^2$
probabilità di lavorare.
I giorni lavorati da ciascuna di quelle 2 persone saranno
giorni lavorati per persona = $\displaystyle 365\cdot\left(\frac{364}{365}\right)^2=363$
giorni totali = $\displaystyle2\cdot363=726$
---
3) Assume 3 persone.
In tal caso, per ogni giorno dell'anno entrambe le persone hanno
$\displaystyle p(3)=\left(\frac{364}{365}\right)^3$
probabilità di lavorare.
I giorni lavorati da ciascuna di quelle 3 persone saranno
giorni lavorati per persona = $\displaystyle 365\cdot\left(\frac{364}{365}\right)^3=362$
giorni totali = $\displaystyle 3\cdot362=1086$
---
E così via, fino a n...
---
n) Assume n persone.
In tal caso, per ogni giorno dell'anno tutte le persone hanno
$\displaystyle p(n)=\left(\frac{364}{365}\right)^n$
probabilità di lavorare.
I giorni lavorati da ciascuna di quelle n persone saranno
giorni lavorati per persona = $\displaystyle 365\cdot\left(\frac{364}{365}\right)^n=...$
giorni totali = $\displaystyle n\cdot365\cdot \left( \frac{364}{365}\right) ^n$
---
Facciamo disegnare il grafico della funzione, ottenendo:
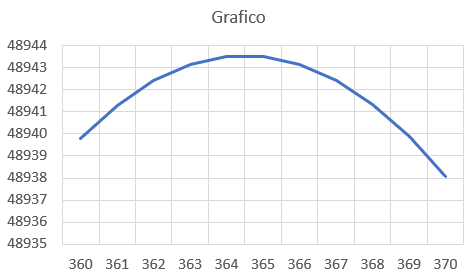
- grafico.png (16.43 KiB) Visto 58712 volte
Dal grafico risulta che le persone sono circa 365 e le giornate lavorate totali sono circa 48943.
---
Salvo errori e omissioni.
Pace e bene a tutti.
Gianfranco
Quanti impiegati deve assumere l'azienda Acme per massimizzare il numero complessivo di giornate lavorate da tutto il suo personale?
)
