intersezione di circonferenze
Moderatori: Gianfranco, Bruno
Questo forum è una sezione del PORTALE DI BASE CINQUE
intersezione di circonferenze
Questo trovo che sia molto carino:
Dati due circoli di raggio unitario intersecati in modo tale che il centro di uno sia appartenente alla circonferenza dell'altro (e viceversa) determinare il perimetro che delimita la figura d'intersezione.
Dati due circoli di raggio unitario intersecati in modo tale che il centro di uno sia appartenente alla circonferenza dell'altro (e viceversa) determinare il perimetro che delimita la figura d'intersezione.
Ah, se i portieri avessero sulla maglia: $|e^{-i\pi}|$...
Pongo $y = x^{2}$ quindi $y=\frac {x^{2}}{pongo}$
[tratto da un compito in classe di uno studente di prima superiore]
Il vero gnomone aureo: http://thumbs.dreamstime.com/z/gnomo-de ... 526933.jpg
Pongo $y = x^{2}$ quindi $y=\frac {x^{2}}{pongo}$
[tratto da un compito in classe di uno studente di prima superiore]
Il vero gnomone aureo: http://thumbs.dreamstime.com/z/gnomo-de ... 526933.jpg
Re: intersezione di circonferenze
Il disegno è scarsetto (l'ho fatto al volo con paint).
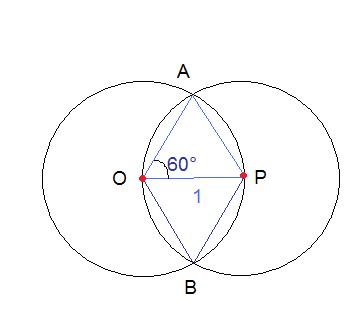
Tutti i lati dei triangoli sono uguali al raggio dei cerchi (=1) quindi ognuno degli archetti (ad esempio AO) è lungo un sesto di circonferenza.
Il perimetro della "losanga" di intersezione, formato da 4 archetti, è quindi pari a 2/3 di circonferenza ossia 4pi/3.
A meno che non abbia capito male il problema.
ciao

Tutti i lati dei triangoli sono uguali al raggio dei cerchi (=1) quindi ognuno degli archetti (ad esempio AO) è lungo un sesto di circonferenza.
Il perimetro della "losanga" di intersezione, formato da 4 archetti, è quindi pari a 2/3 di circonferenza ossia 4pi/3.
A meno che non abbia capito male il problema.
ciao
Franco
ENGINEER
noun. (en-juh-neer)
someone who does precision guesswork based on unreliable data provided by those of questionable knowledge.
See also wizard, magician
ENGINEER
noun. (en-juh-neer)
someone who does precision guesswork based on unreliable data provided by those of questionable knowledge.
See also wizard, magician
Re: intersezione di circonferenze
Perfetto, ora posso aggiungere la seconda parte del problema:
Trovare l'area della "losanga" e dire:
1) In che rapporto sta il suo perimetro con la circonferenza di un circolo con cerchio congruente all'area della "losanga".
2) In che rapporto sta la sua area con il cerchio di un circolo con circonferenza congruente al perimetro della "losanga".
P.S. Il testo originale ometteva la domanda della prima parte (a cui hai già risposto): l'ho aggiunta per propedeuticità, poichè non tutti i miei ragazzi riescono ancora a camminare da soli quando si tratta di gestire cerchi e circonferenze .
.
P.S.S. Ho usato il tuo termine "losanga" per maggior chiarezza.
P.S.S.S. Secondo voi dovrei aggiungere altre domande intermedie per meglio guidarli verso la soluzione?
Trovare l'area della "losanga" e dire:
1) In che rapporto sta il suo perimetro con la circonferenza di un circolo con cerchio congruente all'area della "losanga".
2) In che rapporto sta la sua area con il cerchio di un circolo con circonferenza congruente al perimetro della "losanga".
P.S. Il testo originale ometteva la domanda della prima parte (a cui hai già risposto): l'ho aggiunta per propedeuticità, poichè non tutti i miei ragazzi riescono ancora a camminare da soli quando si tratta di gestire cerchi e circonferenze
P.S.S. Ho usato il tuo termine "losanga" per maggior chiarezza.
P.S.S.S. Secondo voi dovrei aggiungere altre domande intermedie per meglio guidarli verso la soluzione?
Ah, se i portieri avessero sulla maglia: $|e^{-i\pi}|$...
Pongo $y = x^{2}$ quindi $y=\frac {x^{2}}{pongo}$
[tratto da un compito in classe di uno studente di prima superiore]
Il vero gnomone aureo: http://thumbs.dreamstime.com/z/gnomo-de ... 526933.jpg
Pongo $y = x^{2}$ quindi $y=\frac {x^{2}}{pongo}$
[tratto da un compito in classe di uno studente di prima superiore]
Il vero gnomone aureo: http://thumbs.dreamstime.com/z/gnomo-de ... 526933.jpg
Re: intersezione di circonferenze
che intendi per losanga?
la zona di piano in comune ai due cerchi?
in tal caso la chiamerei "mandorla", come lìelemento decorativo architettonico
la zona di piano in comune ai due cerchi?
in tal caso la chiamerei "mandorla", come lìelemento decorativo architettonico
Enrico
Re: intersezione di circonferenze
Delfo, penso che si riferisca al rombo AOBP del disegno di Franco.
_________________
$\text { }$ciao ciao
ciao
E' la somma che fa il totale (Totò)
$\text { }$ciao
E' la somma che fa il totale (Totò)
Re: intersezione di circonferenze
Poiché la parola “losanga” è stata scritta tra virgolette e, inoltre, come ha precisato Franco, si tratta di “losanga” di intersezione il cui contorno è formato da “4 archetti”, ritengo che anche Fab voglia riferirsi alla figura geometrica costituita dal segmento circolare a una base con il suo simmetrico rispetto alla base stessa…
Forse Franco ha chiamato “losanga” tale figura immaginandola come un rombo con i lati curvilinei…
Forse Franco ha chiamato “losanga” tale figura immaginandola come un rombo con i lati curvilinei…

"L'essenza della matematica è la libertà" (Georg Cantor)
Re: intersezione di circonferenze
Ho usato "losanga" intendendo effettivamente la "mandorla" ossia la figura di intersezione delle due circonferenze.
Purtroppo è qualche tempo che riesco a malapena a trovare un minuto ogni tanto per Base5; in questo caso non l'ho sprecato per cercare una definizione migliore
ciao
Purtroppo è qualche tempo che riesco a malapena a trovare un minuto ogni tanto per Base5; in questo caso non l'ho sprecato per cercare una definizione migliore
ciao
Franco
ENGINEER
noun. (en-juh-neer)
someone who does precision guesswork based on unreliable data provided by those of questionable knowledge.
See also wizard, magician
ENGINEER
noun. (en-juh-neer)
someone who does precision guesswork based on unreliable data provided by those of questionable knowledge.
See also wizard, magician
Re: intersezione di circonferenze
Confermo che il termine losanga lo preso "in prestito" da Franco per indicare la superfice di intersezione tra i 2 circoli visto che tale termine era stato da lui introdotto per risolvere la prima parte del quesito così da non usare il più articolato (e barocco, a mio avviso) "superfice d'intersezione tra i due circoli" che rendeva meno scorrevole il testo.
Riflessioni/congetture
In generale, posso aggiungere che ad un'analisi approssimativa (poichè frutto solo di un esperimento mentale non coadiuvato da carta e penna) direi che il fatto che i due raggi siano congruenti implica "l'isoscelità" del triangolo OAO' (e del suo simmetrico OBO') mentre la condizione più forte di "equilaterità" è implicata dal fatto che un centro sia punto della circonferenza che ha come centro l'altro, e viceversa.
Quindi se queste mie elucubrazioni sono corrette direi che con un po' di analisi potremmo tranquillamente trovare una formula generale per tutte le "losanghe francofone" generate da un intersezione di qualunque coppia di circoli indipendentemente dal fatto che sussistano sia la condizione di "equilateralità" del triangolo OAO' sia quella di "isoscelità" dello stesso, (ma questo ai miei ragazzi non è richiesto, beh non ancora almeno ).
).
Riflessioni/congetture
In generale, posso aggiungere che ad un'analisi approssimativa (poichè frutto solo di un esperimento mentale non coadiuvato da carta e penna) direi che il fatto che i due raggi siano congruenti implica "l'isoscelità" del triangolo OAO' (e del suo simmetrico OBO') mentre la condizione più forte di "equilaterità" è implicata dal fatto che un centro sia punto della circonferenza che ha come centro l'altro, e viceversa.
Quindi se queste mie elucubrazioni sono corrette direi che con un po' di analisi potremmo tranquillamente trovare una formula generale per tutte le "losanghe francofone" generate da un intersezione di qualunque coppia di circoli indipendentemente dal fatto che sussistano sia la condizione di "equilateralità" del triangolo OAO' sia quella di "isoscelità" dello stesso, (ma questo ai miei ragazzi non è richiesto, beh non ancora almeno
Ah, se i portieri avessero sulla maglia: $|e^{-i\pi}|$...
Pongo $y = x^{2}$ quindi $y=\frac {x^{2}}{pongo}$
[tratto da un compito in classe di uno studente di prima superiore]
Il vero gnomone aureo: http://thumbs.dreamstime.com/z/gnomo-de ... 526933.jpg
Pongo $y = x^{2}$ quindi $y=\frac {x^{2}}{pongo}$
[tratto da un compito in classe di uno studente di prima superiore]
Il vero gnomone aureo: http://thumbs.dreamstime.com/z/gnomo-de ... 526933.jpg
Re: intersezione di circonferenze
In realta non è molto difficile
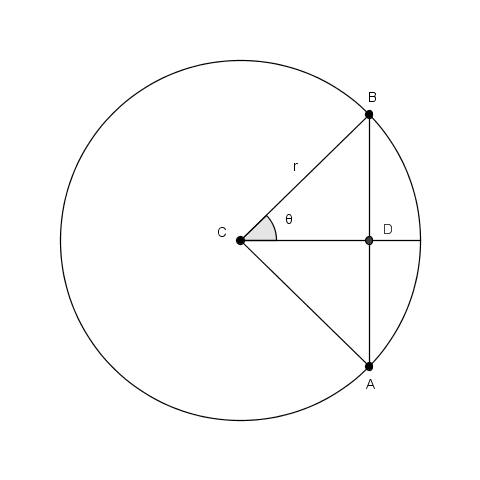
la corda ${\text AB}$ delimita un segmento circolare la cui area è data dalla differenza tra l'area del settore circolare e quella del triangolo ${\text ABC}$.
In funzione di $r$ e $\theta$
$A\/=\/\frac {r^{\script 2}}2\/\left(2\theta\/-\/\sin2\theta\right)$
Se poi ${\text AB}$ è la corda anche di un secondo cerchio
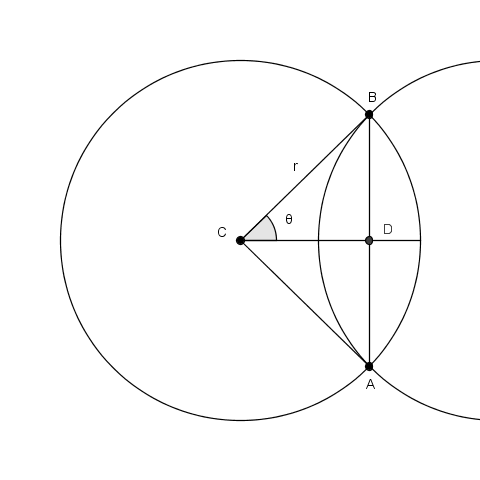
l'area della "losanga" è la somma dei due segmenti circolari (che possono anche essere diversi).
P.S.: mathmum, dove sei? Come faccio per colorare l'intersezione di due cerchi in GeoGebra?

la corda ${\text AB}$ delimita un segmento circolare la cui area è data dalla differenza tra l'area del settore circolare e quella del triangolo ${\text ABC}$.
In funzione di $r$ e $\theta$
$A\/=\/\frac {r^{\script 2}}2\/\left(2\theta\/-\/\sin2\theta\right)$
Se poi ${\text AB}$ è la corda anche di un secondo cerchio

l'area della "losanga" è la somma dei due segmenti circolari (che possono anche essere diversi).
P.S.: mathmum, dove sei? Come faccio per colorare l'intersezione di due cerchi in GeoGebra?
il panurgo
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
Re: intersezione di circonferenze
@ Panurgo: Beh, essendo la versione con raggio unitario un problema per le terze medie non poteva essere troppo difficile, no?
Ah, se i portieri avessero sulla maglia: $|e^{-i\pi}|$...
Pongo $y = x^{2}$ quindi $y=\frac {x^{2}}{pongo}$
[tratto da un compito in classe di uno studente di prima superiore]
Il vero gnomone aureo: http://thumbs.dreamstime.com/z/gnomo-de ... 526933.jpg
Pongo $y = x^{2}$ quindi $y=\frac {x^{2}}{pongo}$
[tratto da un compito in classe di uno studente di prima superiore]
Il vero gnomone aureo: http://thumbs.dreamstime.com/z/gnomo-de ... 526933.jpg
Re: intersezione di circonferenze
Intendi "colorare" così?:panurgo ha scritto:[...]
P.S.: mathmum, dove sei? Come faccio per colorare l'intersezione di due cerchi in GeoGebra?
- Allegati
-
- intersezione_due_cerchi.gif (5.52 KiB) Visto 19532 volte

"L'essenza della matematica è la libertà" (Georg Cantor)
Re: intersezione di circonferenze
mais oui! 
il panurgo
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
Re: intersezione di circonferenze
OK, Pan, tra poco ti invio un messaggio privato...panurgo ha scritto:mais oui!
A presto
Ivana
Edito per precisare che il messaggio privato mi rimane in uscita... Ti ho inviato il messaggio tramite posta elettronica, ma ho ricevuto subito quanto segue:
Delivery to the following recipient failed permanently:
[...]
Technical details of permanent failure:
DNS Error: Domain name not found

"L'essenza della matematica è la libertà" (Georg Cantor)
Re: intersezione di circonferenze
Il messaggio rimane in uscita fino a che non viene letto dal destinatario: grazie mille! Ecco comunque ciò intendevo
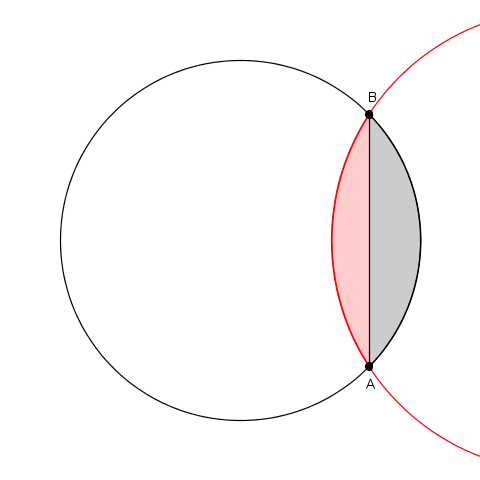

il panurgo
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
Re: intersezione di circonferenze
Partendo da quanto finora detto rendiamo il tutto un filino più complicato (ma non troppo) quindi al posto di considerare i due circoli sostituiamoli con due ellissi dove considerando i fuochi prossimali delle due ellissi questi giaciono ognuno sull'altra ellisse. La domanda è sempre la solita trovare l'area dell'intersezione.
In aggiunta: Qual è la condizione necessaria affinchè l'angolo tra il semiasse maggiore e il segmento che congiunge il punto medio tra i fuochi e uno dei due punti di intersezione delle due ellissi sia di 60°?
In aggiunta: Qual è la condizione necessaria affinchè l'angolo tra il semiasse maggiore e il segmento che congiunge il punto medio tra i fuochi e uno dei due punti di intersezione delle due ellissi sia di 60°?
Ah, se i portieri avessero sulla maglia: $|e^{-i\pi}|$...
Pongo $y = x^{2}$ quindi $y=\frac {x^{2}}{pongo}$
[tratto da un compito in classe di uno studente di prima superiore]
Il vero gnomone aureo: http://thumbs.dreamstime.com/z/gnomo-de ... 526933.jpg
Pongo $y = x^{2}$ quindi $y=\frac {x^{2}}{pongo}$
[tratto da un compito in classe di uno studente di prima superiore]
Il vero gnomone aureo: http://thumbs.dreamstime.com/z/gnomo-de ... 526933.jpg




