La soluzione di Quelo è migliorabile facendo scorrere lungo i lati del triangolo equilatero i due triangoli isosceli laterali fino al contatto con la base.
Questo accorgimento ci permette di aumentare leggermente l'angolo $\theta$ al vertice dei triangoli isosceli e quindi la loro area che è: $A=\sqrt3 tan(\frac \theta 2) $.
L'area massima da me trovata è l'unica soluzione di questa equazione di decimo grado compresa nei limiti geometrici del problema: $$A^{10}-10A^9-67A^8+504A^7+1170A^6-2508A^5-654A^4+1368A^3-531A^2-378A+81=0 $$ Essa è: $ A=0.185645...$
Triangolo diviso in 5 triangoli congruenti
Moderatori: Gianfranco, Bruno
Questo forum è una sezione del PORTALE DI BASE CINQUE
-
Maurizio59
- Livello 3

- Messaggi: 78
- Iscritto il: mar lug 26, 2022 9:02 am
Re: Triangolo diviso in 5 triangoli congruenti
Bravo, non ci avevo pensato.
Se facciamo traslare i triangoli esterni e li ruotiamo fino ad allinearsi ai lati del triangolo equilatero, possiamo massimizzare l'angolo al vertice.
Applicado un po' di trigonometria si ricava questa formula:
$\displaystyle 2\sin{\left(\frac{\pi+\alpha}{2}\right)}\tan{\left(\frac{\alpha}{2}\right)}+\frac{\sqrt{3}\sin{\left(\frac{2}{3}\pi-2\alpha\right)\tan{\left(\frac{\alpha}{2}\right)}}}{\sin{\left(\frac{1}{3}\pi+\alpha\right)}}+\frac{\sqrt{3}}{2}\tan{\left(\frac{\alpha}{2}\right)}=\frac12$
da cui si ricava $\alpha = 0,2135486$ e $A=0,185645$
A questo punto, perché non mettere 5 triangoli in un quadrato?
Se facciamo traslare i triangoli esterni e li ruotiamo fino ad allinearsi ai lati del triangolo equilatero, possiamo massimizzare l'angolo al vertice.
Applicado un po' di trigonometria si ricava questa formula:
$\displaystyle 2\sin{\left(\frac{\pi+\alpha}{2}\right)}\tan{\left(\frac{\alpha}{2}\right)}+\frac{\sqrt{3}\sin{\left(\frac{2}{3}\pi-2\alpha\right)\tan{\left(\frac{\alpha}{2}\right)}}}{\sin{\left(\frac{1}{3}\pi+\alpha\right)}}+\frac{\sqrt{3}}{2}\tan{\left(\frac{\alpha}{2}\right)}=\frac12$
da cui si ricava $\alpha = 0,2135486$ e $A=0,185645$
A questo punto, perché non mettere 5 triangoli in un quadrato?
[Sergio] / $17$
-
Maurizio59
- Livello 3

- Messaggi: 78
- Iscritto il: mar lug 26, 2022 9:02 am
-
Maurizio59
- Livello 3

- Messaggi: 78
- Iscritto il: mar lug 26, 2022 9:02 am
Re: Triangolo diviso in 5 triangoli congruenti
...
Ho trovato una bella configurazione formata da cinque triangoli rettangoli di ipotenusa 1.
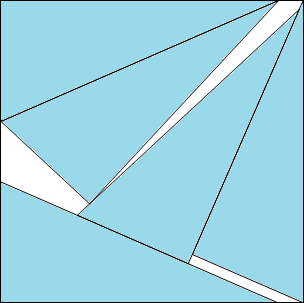
L'area di un triangolo si trova risolvendo la seguente equazione di ottavo grado:$$1048576A^8-57344A^6-752A^4+80A^2-1=0 $$ Nell'intervallo geometrico ammissibile ci sono due soluzioni e quella cercata è la minore. Essa è: $A=0.183425...$
Ho trovato una bella configurazione formata da cinque triangoli rettangoli di ipotenusa 1.

L'area di un triangolo si trova risolvendo la seguente equazione di ottavo grado:$$1048576A^8-57344A^6-752A^4+80A^2-1=0 $$ Nell'intervallo geometrico ammissibile ci sono due soluzioni e quella cercata è la minore. Essa è: $A=0.183425...$

