Quadrato e Ottagono
Moderatori: Gianfranco, Bruno
Questo forum è una sezione del PORTALE DI BASE CINQUE
Quadrato e Ottagono
Dato un quadrato di lato l, costruire solo con l'ausilio di riga e squadra un ottagono regolare la cui circonferenza circoscritta abbia il centro nel punto di intersezione delle diagonali del quadrato e la cui superficie sia 1/6 del quadrato stesso.
Ah, se i portieri avessero sulla maglia: $|e^{-i\pi}|$...
Pongo $y = x^{2}$ quindi $y=\frac {x^{2}}{pongo}$
[tratto da un compito in classe di uno studente di prima superiore]
Il vero gnomone aureo: http://thumbs.dreamstime.com/z/gnomo-de ... 526933.jpg
Pongo $y = x^{2}$ quindi $y=\frac {x^{2}}{pongo}$
[tratto da un compito in classe di uno studente di prima superiore]
Il vero gnomone aureo: http://thumbs.dreamstime.com/z/gnomo-de ... 526933.jpg
Re: Quadrato e Ottagono
penso che aiuti trovare il lato dell'ottagono che soddisfa le condizioni
parto dall'ottagono, di cui considero un triangolo formato da uno dei lati e due raggi di circonferenza,
trattandosi di un triangolo isoscele esso corrisponde ad un rettangolo avente per diagonale (di seguito r) il raggio della circonferenza e per altezza (h) meta`del lato dell'ottagono, la base la chiamo b
l'area del rettangolo la trovo facendo b*h, ma non conosco nessuno dei due dati
quindi
$\frac{h}{b}=\tan\(\frac{\pi}{8}\)$
per ogni triangolo
$r^2=b^2+h^2$
$\frac{r^2}{b^2}=1+\tan\(\frac{\pi}{8}\)^2$
$b^2=\frac{r^2}{\(1+\tan\(\frac{\pi}{8}\)^2\)}$
$b=\frac{r}{\sqr{1+\tan\(\frac{\pi}{8}\)^2}}$
ricordo che $\frac{h}{b}=\tan\(\frac{\pi}{8}\)$
quindi
$h\cdot b=\frac{r^2\cdot\tan\(\frac{\pi}{8}\)}{\(1+\tan\(\frac{\pi}{8}\)^2\)}$
ricordando che si tratta di un ottavo dell'area dell'ottagono
$A_{ott}=8\cdot\frac{r^2\cdot\tan\(\frac{\pi}{8}\)}{1+\tan\(\frac{\pi}{8}\)^2}$
l'area della circonferenza circoscritta all'ottagono viene imposta essere 1/6 dell'area del quadrato
$\pi\cdot r^2=\frac{l^2}{6}$
quindi
$r=\frac{l}{\sqr{6\cdot\pi}}$
ricordando che
$b=\frac{r}{\sqr{1+\tan\(\frac{\pi}{8}\)^2}}$
si ottiene
$h=\tan\(\frac{\pi}{8}\)\cdot b=\\=\tan\(\frac{\pi}{8}\)\cdot\frac{r}{\sqr{1+\tan\(\frac{\pi}{8}\)^2}}=\\=\tan\(\frac{\pi}{8}\)\cdot\frac{\frac{l}{\sqr{6\cdot\pi}}}{\sqr{1+\tan\(\frac{\pi}{8}\)^2}}\\h=\tan\(\frac{\pi}{8}\)\cdot\frac{l}{\sqr{6\cdot\pi\cdot\(1+\tan\(\frac{\pi}{8}\)^2\)}$
cioe`il lato del quadrato e`circa 15 volte il lato dell'ottagono.... non vedo spunti per una costruzione con riga e squadra...
parto dall'ottagono, di cui considero un triangolo formato da uno dei lati e due raggi di circonferenza,
trattandosi di un triangolo isoscele esso corrisponde ad un rettangolo avente per diagonale (di seguito r) il raggio della circonferenza e per altezza (h) meta`del lato dell'ottagono, la base la chiamo b
l'area del rettangolo la trovo facendo b*h, ma non conosco nessuno dei due dati
quindi
$\frac{h}{b}=\tan\(\frac{\pi}{8}\)$
per ogni triangolo
$r^2=b^2+h^2$
$\frac{r^2}{b^2}=1+\tan\(\frac{\pi}{8}\)^2$
$b^2=\frac{r^2}{\(1+\tan\(\frac{\pi}{8}\)^2\)}$
$b=\frac{r}{\sqr{1+\tan\(\frac{\pi}{8}\)^2}}$
ricordo che $\frac{h}{b}=\tan\(\frac{\pi}{8}\)$
quindi
$h\cdot b=\frac{r^2\cdot\tan\(\frac{\pi}{8}\)}{\(1+\tan\(\frac{\pi}{8}\)^2\)}$
ricordando che si tratta di un ottavo dell'area dell'ottagono
$A_{ott}=8\cdot\frac{r^2\cdot\tan\(\frac{\pi}{8}\)}{1+\tan\(\frac{\pi}{8}\)^2}$
l'area della circonferenza circoscritta all'ottagono viene imposta essere 1/6 dell'area del quadrato
$\pi\cdot r^2=\frac{l^2}{6}$
quindi
$r=\frac{l}{\sqr{6\cdot\pi}}$
ricordando che
$b=\frac{r}{\sqr{1+\tan\(\frac{\pi}{8}\)^2}}$
si ottiene
$h=\tan\(\frac{\pi}{8}\)\cdot b=\\=\tan\(\frac{\pi}{8}\)\cdot\frac{r}{\sqr{1+\tan\(\frac{\pi}{8}\)^2}}=\\=\tan\(\frac{\pi}{8}\)\cdot\frac{\frac{l}{\sqr{6\cdot\pi}}}{\sqr{1+\tan\(\frac{\pi}{8}\)^2}}\\h=\tan\(\frac{\pi}{8}\)\cdot\frac{l}{\sqr{6\cdot\pi\cdot\(1+\tan\(\frac{\pi}{8}\)^2\)}$
cioe`il lato del quadrato e`circa 15 volte il lato dell'ottagono.... non vedo spunti per una costruzione con riga e squadra...
Re: Quadrato e Ottagono
ok.... dimenticavo che h e`meta`del lato dell'ottagono... quindi il lato del quadrato e`circa 15 volte h, quindi circa 7.5 volte il lato dell'ottagono
Re: Quadrato e Ottagono
ad essere 1/6 dell'area del quadrato è la circonferenza circoscritta all'ottagono (come scrive Info)? o l'ottagono stesso (come avevo interpretato io)?
Enrico
Re: Quadrato e Ottagono
Ritengo chiaro il testo del problema che recita tra l'altro: "[...] un ottagono regolare la cui circonferenza circoscritta abbia il centro nel punto di intersezione delle diagonali del quadrato e la cui superficie sia 1/6 del quadrato stesso.
"la cui circonferenza" = la circonferenza dell'ottagono regolare
"e la cui superficie" = la superficie dell'ottagono regolare
Credo che, approssimativamente parlando, il raggio della circonf. circoscritta all'ottagono regolare dovrebbe essere poco più di 1/3 della semidiagonale del quadrato.
il raggio della circonf. circoscritta all'ottagono regolare dovrebbe essere poco più di 1/3 della semidiagonale del quadrato.
"la cui circonferenza" = la circonferenza dell'ottagono regolare
"e la cui superficie" = la superficie dell'ottagono regolare
Credo che, approssimativamente parlando,

"L'essenza della matematica è la libertà" (Georg Cantor)
Re: Quadrato e Ottagono
Sempre approssimativamente parlando, ecco una rappresentazione grafica... L'arrotondamento è a due cifre decimali.
- Allegati
-
- quadrato_e_ottagono.gif (17.51 KiB) Visto 16047 volte

"L'essenza della matematica è la libertà" (Georg Cantor)
Re: Quadrato e Ottagono
ok, effettivamente.... rileggendo il testo non mi restsa che dare ragione ad Ivana.Ivana ha scritto:Ritengo chiaro il testo del problema che recita tra l'altro: "[...] un ottagono regolare la cui circonferenza circoscritta abbia il centro nel punto di intersezione delle diagonali del quadrato e la cui superficie sia 1/6 del quadrato stesso.
"la cui circonferenza" = la circonferenza dell'ottagono regolare
"e la cui superficie" = la superficie dell'ottagono regolare
Dunque
$A_{ott}=8\cdot\frac{r^2\cdot\tan\(\frac{\pi}{8}\)}{1+\tan\(\frac{\pi}{8}\)^2}=\frac16\cdot l^2$
$r=l\cdot\sqr{\frac{\(1+\tan\(\frac{\pi}{8}\)^2\)}{48\cdot\tan\(\frac{\pi}{8}\)}}$
$h=\tan\(\frac{\pi}{8}\)\cdot b=\\=\tan\(\frac{\pi}{8}\)\cdot\frac{r}{\sqr{1+\tan\(\frac{\pi}{8}\)^2}}=\\=\tan\(\frac{\pi}{8}\)\cdot\frac{l\cdot\sqr{\frac{\(1+\tan\(\frac{\pi}{8}\)^2\)}{48\cdot\tan\(\frac{\pi}{8}\)}}}{\sqr{1+\tan\(\frac{\pi}{8}\)^2}}=\\=\tan\(\frac{\pi}{8}\)\cdot l\cdot\sqr{\frac{\(1+\tan\(\frac{\pi}{8}\)^2\)}{48\cdot\tan\(\frac{\pi}{8}\)\cdot\(1+\tan\(\frac{\pi}{8}\)^2\)}}\\h=l\cdot\sqr{\frac{\tan\(\frac{\pi}{8}\)}{48}$
il lato dell'ottagono e`il doppio, quindi
$l_{ott}=l\cdot\sqr{\frac{\tan\(\frac{\pi}{8}\)}{12}$
quindi il lato del quadrato e`circa 5.38 volte il lato dell'ottagono
adesso ci siamo
complimenti ad Ivana per la costruzione geometrica
Re: Quadrato e Ottagono
Domanda:
Prendendo spunto dal disegno di Ivana Se al posto di tracciare le due diagonali congiungo ogni vertice con il punto medio dei lati la cui intersezione cosa ottengo?
Prendendo spunto dal disegno di Ivana Se al posto di tracciare le due diagonali congiungo ogni vertice con il punto medio dei lati la cui intersezione cosa ottengo?
Ah, se i portieri avessero sulla maglia: $|e^{-i\pi}|$...
Pongo $y = x^{2}$ quindi $y=\frac {x^{2}}{pongo}$
[tratto da un compito in classe di uno studente di prima superiore]
Il vero gnomone aureo: http://thumbs.dreamstime.com/z/gnomo-de ... 526933.jpg
Pongo $y = x^{2}$ quindi $y=\frac {x^{2}}{pongo}$
[tratto da un compito in classe di uno studente di prima superiore]
Il vero gnomone aureo: http://thumbs.dreamstime.com/z/gnomo-de ... 526933.jpg
Re: Quadrato e Ottagono
Grazie, Info, ma meriti tu i complimenti per i calcoli...
Io avevo soltanto constatato che considerando il raggio della circonferenza circoscritta come 1/3 della semidiagonale del quadrato non costruivo un ottagono regolare la cui area fosse esattamente 1/6 dell'area del quadrato e sono ricorsa alla costruzione approssimativa...
Costruendo come suggerito da fabtor, ho realizzato sì un ottagono la cui area è esattamente 1/6 dell'area del quadrato, ma non mi risulta come ottagono regolare...
Ecco la costruzione:
Io avevo soltanto constatato che considerando il raggio della circonferenza circoscritta come 1/3 della semidiagonale del quadrato non costruivo un ottagono regolare la cui area fosse esattamente 1/6 dell'area del quadrato e sono ricorsa alla costruzione approssimativa...
Costruendo come suggerito da fabtor, ho realizzato sì un ottagono la cui area è esattamente 1/6 dell'area del quadrato, ma non mi risulta come ottagono regolare...
Ecco la costruzione:
- Allegati
-
- ottagono.gif (18.58 KiB) Visto 16008 volte

"L'essenza della matematica è la libertà" (Georg Cantor)
Re: Quadrato e Ottagono
Umh, facendolo su carta quadrettata mi pareva di si!
Probabilmente sono incappato in un errore del tipo di quello del "quadrato mancante" del finto triangolo rettangolo, sgrunt !!!
D'altronde devo avere anche qualche problemino di vista, visto che a me il tuo quadrato sembra un rettangolo con base leggermente minore dell'altezza (tra un po' dovrò scrivere al pc con l'aiuto di un cane lupo!!!! (Ri-sgrunt!!!! )
)
Probabilmente sono incappato in un errore del tipo di quello del "quadrato mancante" del finto triangolo rettangolo, sgrunt !!!
D'altronde devo avere anche qualche problemino di vista, visto che a me il tuo quadrato sembra un rettangolo con base leggermente minore dell'altezza (tra un po' dovrò scrivere al pc con l'aiuto di un cane lupo!!!! (Ri-sgrunt!!!!
Ah, se i portieri avessero sulla maglia: $|e^{-i\pi}|$...
Pongo $y = x^{2}$ quindi $y=\frac {x^{2}}{pongo}$
[tratto da un compito in classe di uno studente di prima superiore]
Il vero gnomone aureo: http://thumbs.dreamstime.com/z/gnomo-de ... 526933.jpg
Pongo $y = x^{2}$ quindi $y=\frac {x^{2}}{pongo}$
[tratto da un compito in classe di uno studente di prima superiore]
Il vero gnomone aureo: http://thumbs.dreamstime.com/z/gnomo-de ... 526933.jpg
Re: Quadrato e Ottagono
Ho realizzato la costruzione con geogebra e mi fido abbastanza di tale software...
- Allegati
-
- ottagono.gif (17.85 KiB) Visto 15991 volte

"L'essenza della matematica è la libertà" (Georg Cantor)
Re: Quadrato e Ottagono
Si-si, non mettevo in dubbio la figura: ho semplicemente avuto un'ulteriore conferma che devo proprio mettermi gli occhiali o che cmq non posso più fidarmi al 100% della mia vista!
Ah, se i portieri avessero sulla maglia: $|e^{-i\pi}|$...
Pongo $y = x^{2}$ quindi $y=\frac {x^{2}}{pongo}$
[tratto da un compito in classe di uno studente di prima superiore]
Il vero gnomone aureo: http://thumbs.dreamstime.com/z/gnomo-de ... 526933.jpg
Pongo $y = x^{2}$ quindi $y=\frac {x^{2}}{pongo}$
[tratto da un compito in classe di uno studente di prima superiore]
Il vero gnomone aureo: http://thumbs.dreamstime.com/z/gnomo-de ... 526933.jpg
Re: Quadrato e Ottagono
Il problema può essere diviso in due parti: prima costruire un quadrato che abbia un’area pari ad un sesto dell’area del quadrato di partenza e poi costruire un ottagono equivalente a detto quadrato.
La prima parte non presenta difficoltà: ecco a voi la radice sintetica di $6$
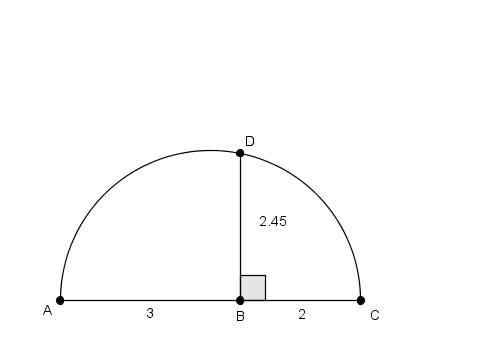
Concentriamoci dunque sulla seconda.
Ecco un quadrato con un ottagono equivalente (GeoGebra esegue i calcoli con un precisione finita ma molto buona: prima del $7$ ci sono tredici $9$)

Dovrebbe essere evidente che grazie agli elementi di simmetria che l’ottagono ha in comune con il quadrato è sufficiente considerare ciò che avviene nel primo ottante: per dimostrare che il quadrato e l’ottagono sono equivalenti è sufficiente farlo per il triangolo rettangolo ${\text ABC}$ e per il triangolo isoscele ${\text ADE}$
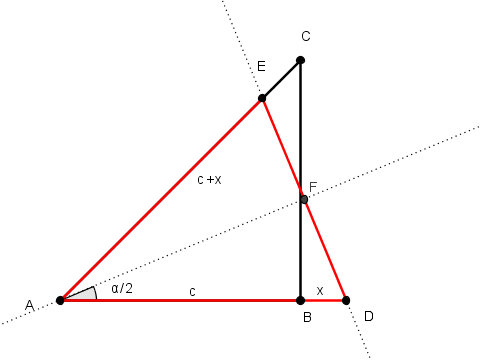
Cominciamo con un po’ di analisi. L’area del primo triangolo vale
${\text ABC}\/=\/\frac{c^{\script 2}}2$
mentre quella del secondo vale
${\text ADE}\/=\/2\/\frac{{\text AF}\times{\text EF}}2\/=\/2\/\frac{\left(c+x\right)\cos\frac\alpha 2\times\left(c+x\right)\sin\frac\alpha 2} 2\/=\/\frac{\left(c+x\right)^{\script 2}} 2\/2\/\sin\frac\alpha 2 \/\cos\frac\alpha 2 \/=\/\frac{\left(c+x\right)^{\script 2}} 2\/\sin\alpha\/=\/\frac{\sqrt{2}\left(c+x\right)^{\script 2}} 4$
Eguagliando le due aree si ottiene l’equazione
$x^{\script 2}\/+\/2\/c\/x\/-\/\left(\sqrt{2}\/-\/1\right)\/c^{\script 2}\/=\/0$
dalla quale, con pochi passaggi di facile algebra si ottiene
$c\/+\/x\/=\/\sqr[4]{2}\/c$
valore da me usato nei disegni precedenti: rispetto alla diagonale del quadrato grande il raggio del cerchio circoscritto all’ottagono vale
$\frac r {\sqrt{2}l} \/=\/\frac 1 {\sqr[4]{72}}\/=\/1\/:\/2,912\ldots$
Tutto ciò non risponde, ahimé, al quesito di fabtor che richiede invece una soluzione sintetica...
P.S.: ecco (segmento $\overline{\text BE}$) la radice quarta sintetica di $2$
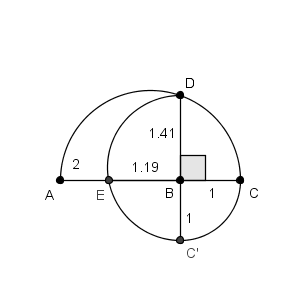
La prima parte non presenta difficoltà: ecco a voi la radice sintetica di $6$

Concentriamoci dunque sulla seconda.
Ecco un quadrato con un ottagono equivalente (GeoGebra esegue i calcoli con un precisione finita ma molto buona: prima del $7$ ci sono tredici $9$)

Dovrebbe essere evidente che grazie agli elementi di simmetria che l’ottagono ha in comune con il quadrato è sufficiente considerare ciò che avviene nel primo ottante: per dimostrare che il quadrato e l’ottagono sono equivalenti è sufficiente farlo per il triangolo rettangolo ${\text ABC}$ e per il triangolo isoscele ${\text ADE}$

Cominciamo con un po’ di analisi. L’area del primo triangolo vale
${\text ABC}\/=\/\frac{c^{\script 2}}2$
mentre quella del secondo vale
${\text ADE}\/=\/2\/\frac{{\text AF}\times{\text EF}}2\/=\/2\/\frac{\left(c+x\right)\cos\frac\alpha 2\times\left(c+x\right)\sin\frac\alpha 2} 2\/=\/\frac{\left(c+x\right)^{\script 2}} 2\/2\/\sin\frac\alpha 2 \/\cos\frac\alpha 2 \/=\/\frac{\left(c+x\right)^{\script 2}} 2\/\sin\alpha\/=\/\frac{\sqrt{2}\left(c+x\right)^{\script 2}} 4$
Eguagliando le due aree si ottiene l’equazione
$x^{\script 2}\/+\/2\/c\/x\/-\/\left(\sqrt{2}\/-\/1\right)\/c^{\script 2}\/=\/0$
dalla quale, con pochi passaggi di facile algebra si ottiene
$c\/+\/x\/=\/\sqr[4]{2}\/c$
valore da me usato nei disegni precedenti: rispetto alla diagonale del quadrato grande il raggio del cerchio circoscritto all’ottagono vale
$\frac r {\sqrt{2}l} \/=\/\frac 1 {\sqr[4]{72}}\/=\/1\/:\/2,912\ldots$
Tutto ciò non risponde, ahimé, al quesito di fabtor che richiede invece una soluzione sintetica...
P.S.: ecco (segmento $\overline{\text BE}$) la radice quarta sintetica di $2$

il panurgo
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
Re: Quadrato e Ottagono
A questo punto, mi sorge il sospetto che l'autore del problema che ho riportato fosse incappato nel mio stesso errore e per risolvere il problema sinteticamente si debba omettere dal testo l'aggettivo regolare.
Sto comunque cercando la scrittura originale per avere lumi in merito.
Sto comunque cercando la scrittura originale per avere lumi in merito.
Ah, se i portieri avessero sulla maglia: $|e^{-i\pi}|$...
Pongo $y = x^{2}$ quindi $y=\frac {x^{2}}{pongo}$
[tratto da un compito in classe di uno studente di prima superiore]
Il vero gnomone aureo: http://thumbs.dreamstime.com/z/gnomo-de ... 526933.jpg
Pongo $y = x^{2}$ quindi $y=\frac {x^{2}}{pongo}$
[tratto da un compito in classe di uno studente di prima superiore]
Il vero gnomone aureo: http://thumbs.dreamstime.com/z/gnomo-de ... 526933.jpg
Re: Quadrato e Ottagono
Mi era mancato il tempo di disegnare la figura...panurgo ha scritto:Il problema può essere diviso in due parti: prima costruire un quadrato che abbia un’area pari ad un sesto dell’area del quadrato di partenza e poi costruire un ottagono equivalente a detto quadrato.
La prima parte non presenta difficoltà [...]
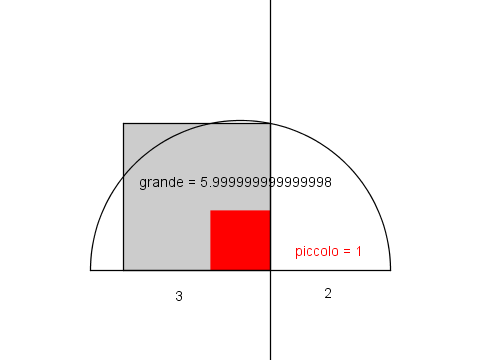
il panurgo
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"



