"Cerchi in un quadrato"

[Quelo]

Dalla sezione "Cerchi in un quadrato"

Cerchi in un triangolo equilatero

Si inscriva una circonferenza in un triangolo equilatero di lato 1 e poi si inscrivano 3 circonferenze in ciascuno dei 3 angoli (tangenti a due lati ed alla precedente circonferenza); quindi si ripeta il procedimento all'infinito (cioè si aggiungano 3 circonferenze sempre più piccole nei 3 angoli).
Calcolare la somma di tutti i cerchi (l'area totale).
Se proprio non volete ripeterlo all'infinito, fatelo almeno per 3 volte!

Nel caso del triangolo vediamo che:

1. Il primo cerchio (principale) ha raggio (r0) pari a 1/3 dell'altezza del triangolo (h)
2. il cerchio principale delimita tre triangoli equilateri (tangente perpendicolare all'altezza) con altezza 1/3 di h
3. i cerchi inscritti in questi triangoli hanno raggio 1/3 di r0
4. ogni nuova serie di cerchi ha raggio 1/3 della precedente

; ;

=== questa parte è stata corretta ===

;





=== fine parte corretta ===



Ragionamento analogo ma meno immediato per il quadrato:
1. il cerchio principale, che ha raggio , delimita 4 triangoli isosceli altezza di
2. i cerchi inscritti in questi triangolo ha raggio
3. ogni nuova serie di cerchi ha raggio volte più piccolo della precedente

;

;







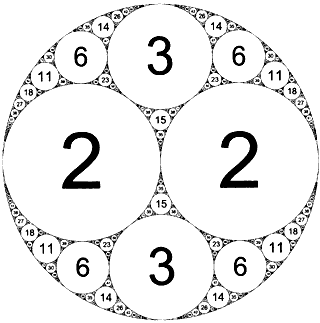
Per quanto riguarda il cerchio, i numeri in figura rappresentano il rapporto tra il raggio del cerchio principale e quello del cerchio che contiene il numero, non vi resta che contarli

SE&O

[Quelo]

P.S. Ho visto adesso che il quadrato era già stato fatto, diversamente da come ho fatto io ma con lo stesso risultato.

[fabiuz]

Il caso col cerchio assomiglia un po' ad un frattale... per curiosità, si riesce a tassellare completamente la figura oppure l'area coperta è sempre inferiore a quella del cerchio completo?

[Daniela]

se il limite dei raggi permessi tende a zero, anche il limite dell'area coperta dovrebbe tendere all'area del cerchio, sono anche loro una simpatica sigma-algebra o meglio lo diventano facilmente; o in maniera piu' intuitiva alla riemann puoi sbarazzarti dei cerchi piccoli sostituendoli con le figure composte di quadratini che approssimano la loro area, se il limite dei raggi permessi tende a zero, tutto quanto si mette apposto

[fabiuz]

mmm...non ho ben capito.
Il problema è che se cerco di calcolare l'area nera di una figura come questa:



viene fuori zero (via via che cancello triangoli sempre più piccoli avrò 3/4*3/4*3/4*....), però è evidente che c'è sempre un'area nera diversa da 0 ad ogni passaggio. All'infinito può quest'area essere effetivamente 0? Immagino di sì, ma non vorrei che fosse una di quelle funzioni il cui limite in un certo punto è diverso dal valore reale.
Con uno scherzetto simile si poteva dimpostrare che pi greco è uguale a 2
http://plus.maths.org/issue40/puzzle/solution.html" onclick="window.open(this.href);return false;

[Daniela]

ma la figura del triangolo ha dei vincoli, si tratta di costruire dei triangolini che hanno i vertici nei punti a 1/3 e 2/3 del segmento, ecc.
O forse sono io che non ho capito la figura quella con i numeri dentro da 2 a 23 e oltre?

[fabiuz]

scusami, ho fatto confusione io
Allora, il quesito originale risolto sopra è OK, chiaro e perfettamente dimostrato da Quelo.

Lasciate perdere la figura che ho postato io, era solo un esempio
Quello che non mi è chiaro è associato alla figura con i cerchi postata sopra, con i numeretti da 2 a 23 e oltre.
La domanda è se effettivamente i cerchi lascino scoperta un'area nulla (come probabilmente è) oppure piccola ma diversa da zero.

Tu hai citato la "sigma-algebra": io purtroppo sono un neofita e non so cosa sia, ma se me lo spieghi te ne sarò grato.