R: "Dissezioni del quadrato" - 5. Per quali n è possibile dividere un quadrato in n quadra

panurgo · Messaggio da **panurgo** » dom dic 11, 2005 10:24 am

Dalla sezione "Dissezioni del quadrato"

4. Dividere un quadrato in 7 quadrati uguali

5. Per quali n è possibile dividere un quadrato in n quadrati uguali?

Il sezionamento di un quadrato di lato $l$ è possibile per qualunque valore di $n$ (almeno in linea di principio).

Infatti, poiché è possibile sezionare un quadrato per ottenere un qualsiasi rettangolo di base $a$ e altezza $b$ date (vedi http://www.base5forum.it/viewtopic.php?p=476#476), basta prendere $a = \sqrt {n} l$ e $b = \frac{l}{\sqrt {n}}$ dove $\frac{l}{\sqrt {n}}$ è il "latino" (memento: "latino × latino = area del quadratino").

Dato che il sezionamento è tanto più facile quanto più il rapporto $r = \frac a b$ tende all’unità, se $n$ non è primo conviene scomporlo in due fattori $p$ e $q$ e prendere $a = p \frac{l}{\sqrt {n}}$ e $b = q \frac{l}{\sqrt {n}}$ (per $p = n$ e $q = 1$ si riottengono le espressioni precedenti).

A questo punto bisogna determinare la lunghezza del "latino", $\frac{l}{\sqrt {n}}$ .

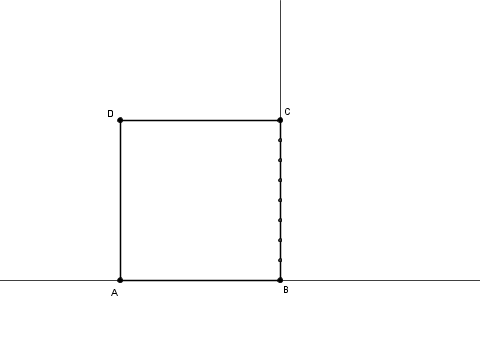
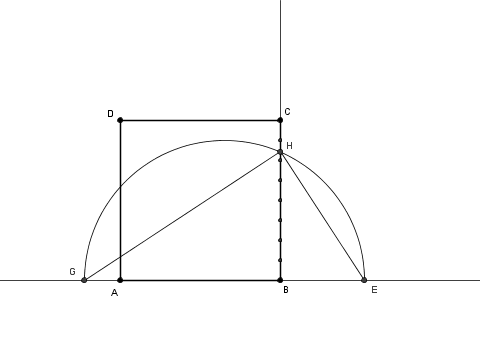
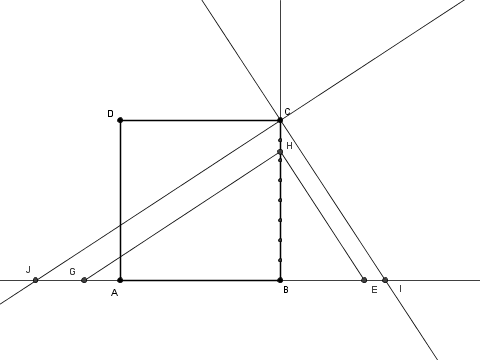
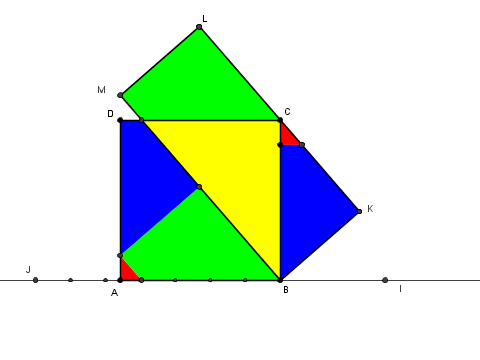
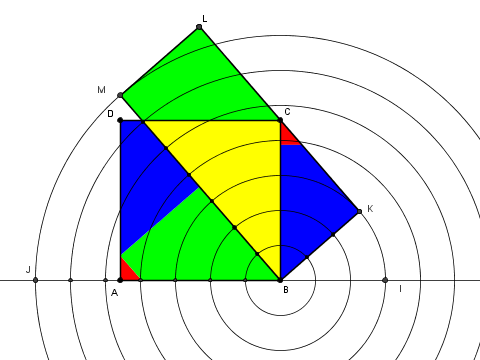
A tale scopo (vedi figura) è sufficiente tracciare la parabola con il vertice in ${\rm A}$ e passante per ${\rm C}$ e l’iperbole equilatera, ruotata di 45°, con il vertice in ${\rm C}$ e centro di simmetria in ${\rm A}$ .

La prima conica ci consente di ottenere la radice quadrata e la seconda, l’inverso di $n$ .

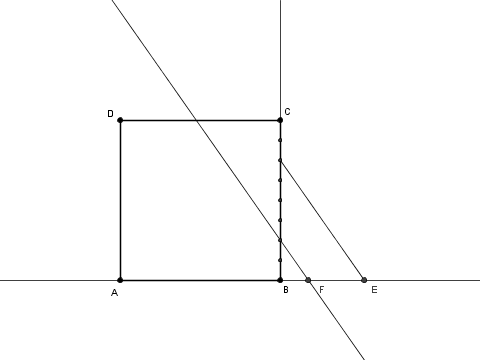
Prendendo ad esempio $n = 2$ , si traccia sul prolungamento del segmento $\overline {\rm AB}$ il punto ${\rm P}$ distante $2l$ da ${\rm A}$

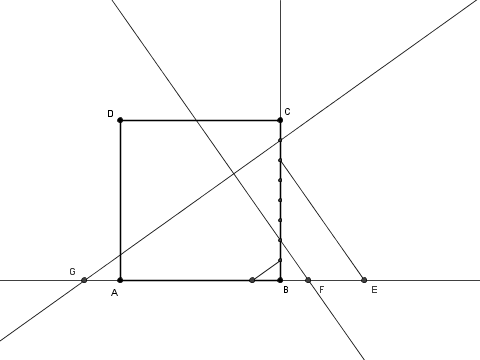
si traccia la parallela a $\overline {\rm BC}$ per ${\rm P}$ e si trova il punto ${\rm Q}$ : si ha $\overline {\rm PQ} = \frac l n$ .

si traccia ora la parallela a $\overline {\rm AB}$ per ${\rm Q}$ e si trovano i punti ${\rm R}$ e ${\rm S}$ : si ha $\overline {\rm RS} = \frac l {\sqrt n}$ .

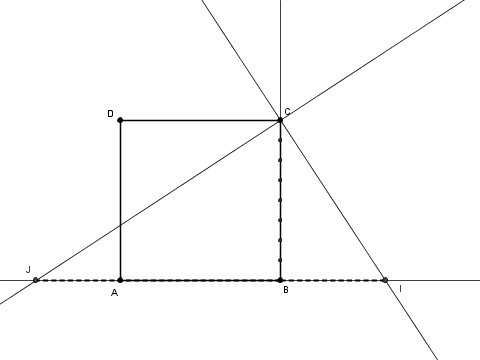
A questo punto si costruisce il rettangolo $ab$ come specificato sopra (vedi link)

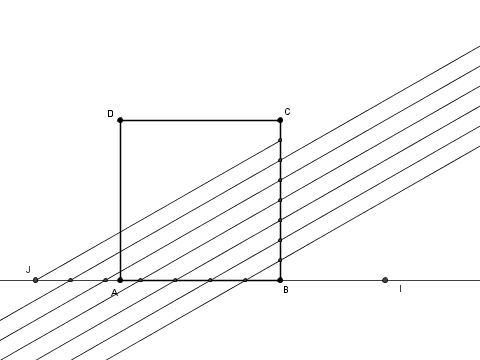
e si procede al sezionamento.

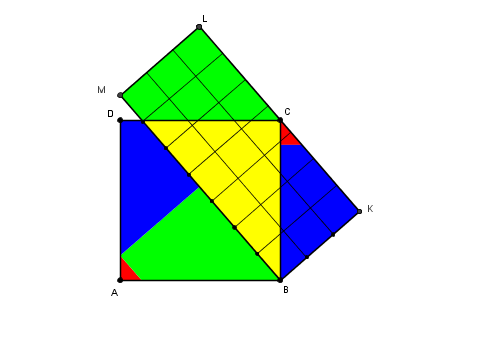
Come altro esempio, prendo il sezionamento del quadrato in sette

Et voilà!

0-§ · Messaggio da **0-§** » mar dic 13, 2005 10:40 pm

Sul vecchio forum era passato inosservato il mio problema,che non so risolvere:quali quadrati perfetti sono la somma dei primi quadrati perfetti?
Cioé vorrei sapere per quali N la somma
$1^2+2^2+3^2+...N^2$ é un quadrato perfetto.Cosa succede se pongo la condizione che i vari quadrati siano sì consecutivi,ma non debbano partire da 1^2?Ad esempio,vorrei sapere quali quadrati perfetti sono la somma di tre,sedici,ottomilacentoventiquattro quadrati perfetti(per il Teorema di Fermat-Wiles,obbligatoriamente più di due quadrati)Come si trovano le varie soluzioni?
E infine la domanda da cento milioni:che succede se anziché quadrati uso cubi o potenze quarte?
Qui c'é mezza Teoria dei numeri e credo non esistano risposte generali a queste domande:vorrei solo sapene un pò di più(se conoscete un posticino su Internet per queste domande,dite pure!).
Per il problema 1,aspetto con ansia risposte (dovrebbe essere alla vostra portata)
Saluti,salute e figli baschi(come dicono in Spagna).
Ciao!

Bruno · Messaggio da **Bruno** » gio dic 15, 2005 11:52 am

0-§ ha scritto: Cioé vorrei sapere per quali N la somma
$\displaystyle 1^2+2^2+3^2+...N^2$ é un quadrato perfetto.

Ciao 0-§! Per quanto ne so, all'inizio del secolo scorso è stato dimostrato
che la somma:

$\displaystyle 1^2+2^2+3^2+...+N^2$

corrisponde a un quadrato perfetto solo per $\displaystyle N = 24$ (se si eccettua
il caso N=1) e il risultato è:

$\displaystyle 70^2 = 4900.$

Non esiste un $\displaystyle N \, > \, 24$ che goda di questa stessa proprietà.

Non so niente, invece, sulle altre interessanti questioni che proponi.

Diversi anni fa mi è capitato fra le mani un libro che considero ancora molto
istruttivo (peraltro uno dei pochi tradotti in italiano). Se già non lo conosci,
vorrei consigliartelo: si tratta di "Aritmetica Superiore" di H. Davenport, edito
da Zanichelli.

Bruno

0-§ · Messaggio da **0-§** » mer dic 21, 2005 5:09 pm

Grazie!Un'altra domanda che mi é sorta:si può coprire il quadrato gigante(di lato 70) completamente e senza tagli con quadratini di lato 1,2,3,...,24?
Se sì,come?Se no,perché?
Bye bye
0-§[/i]

Pasquale · Messaggio da **Pasquale** » mer dic 28, 2005 8:52 pm

un esempio

panurgo · Messaggio da **panurgo** » dom ott 30, 2011 9:24 am

panurgo ha scritto:
Dalla sezione "Dissezioni del quadrato"

4. Dividere un quadrato in 7 quadrati uguali

5. Per quali n è possibile dividere un quadrato in n quadrati uguali?

Il sezionamento di un quadrato di lato $l$ è possibile per qualunque valore di $n$ (almeno in linea di principio).

Le immagini sono andate perdute! Invece di cercare di ricostruirle mi limiterò a sezionare un quadrato in $21$ quadratini.

Dato il quadrato ${\text ABCD}$

Immagine

tracciamo la retta ${\text AB}$ , la semiretta ${\text BC}$ e dividiamo il lato ${\text BC}$ (per bisezione) in $8$ parti

Immagine

Segnamo il punto $\text E$ e lo congiungiamo con il punto a $3/4$ sul lato ${\text BC}$ ; quindi tracciamo la parallela al segmento passante per il punto a $1/4$ individuando così il punto $\text F$ : per il teorema di Talete ${\text BE}\/:\/{\text BF}\/=\/3\/:\/1$ .
Abbiamo misurato ${\text BE}$

Immagine

Riportata la nostra unità di misura simmetricamente a $\text B$ individuiamo, sempre con Talete, il punto $\text G$ per cui ${\text BG}\/:\/{\text BF}\/=\/7\/:\/1$ (suona giusto, $3\/\times\/7\/=\/21$ ).

Immagine

E abbiamo dunque ${\text BG}\/:\/{\text BE}\/=\/7\/:\/3$ ; tracciamo la semicirconferenza da $\text G$ a $\text E$ e individuiamo il punto $\text H$ : per il secondo teorema di Euclide sui triangoli rettangoli ${\text BH}$ è medio proporzionale tra ${\text BG}$ e ${\text BE}$ ed è quindi il lato del quadrato equivalente al rettangolo di lati ${\text BG}$ e ${\text BE}$ (ecco perché si chiama media geometrica)

Immagine

Tracciamo per ${\text C}$ le parallele a ${\text EH}$ e ${\text GH}$ e individuiamo i punti ${\text I}$ e ${\text J}$ , estremi dei segmenti ${\text BI}$ e ${\text BJ}$ che sono i segmenti di cui il lato del nostro quadrato è medio proporzionale (Talete? Euclide 2?)

Immagine

Puliamo il nostro disegno e osserviamo che abbiamo, ${\text BJ}\/:\/{\text BI}\/=\/7\/:\/3$ , i lati del rettangolo equivalente al nostro quadrato e formato da $21$ quadratini.

Immagine

Approfittiamo di questa pulizia per dividere il segmento ${\text BJ}$ in $7$ parti: ci servirà dopo

Immagine

L’intersezione della semicirconferenza da ${\text B}$ a ${\text C}$ con la circonferenza di centro ${\text B}$ e raggio ${\text BI}$ individua il punto ${\text K}$ e l’intersezione della perpendicolare a ${\text BK}$ con la circonferenza di centro ${\text B}$ e raggio ${\text BJ}$ il punto ${\text M}$

Immagine

La ragione di questa costruzione e che in questo modo un lato del rettangolo passa per il punto ${\text C}$ (l’angolo al centro è il doppio dell’angolo alla circonferenza) e ciò è utile per il sezionamento

Immagine

Tracciando la parallela a ${\text BM}$ passante per il punto ${\text L}'$ , simmetrico di ${\text L}$ rispetto a ${\text M}$ tagliamo un triangolo che trasportiamo come indicato il figura

Immagine

La perpendicolare dal vertice del triangolo a ${\text BM}$ taglia un trapezio

Immagine

e un quadrilatero mentre il triangolo comune tra quadrato e rettangolo rimane al suo posto

Immagine

Tutto ciò si dimostra perché tagli sono paralleli ai lati del rettangolo e si ottengono dei parallelogrammi.

Ora non resta che misurare il nostro rettangolo

Immagine

e tagliarlo in $21$ quadratini

Immagine

Questo ci dice come deve essere ritagliato il quadrato per ottenere i quadratini desiderati.

Due considerazioni: la prima è che conviene suddividere $n$ in due fattori quanto più possibile uguali; la seconda è che resta da dimostrare che il sezionamento di un quadrato in un rettangolo qualsiasi è sempre possibile (ma questo è un altro topic).

P.S.: tutte queste figure si ridurrebbero ad un solo foglio di lavoro dinamico di GeoGebra che è ciò che ho usato per generarle!

Messaggio da **Admin** » mar nov 01, 2011 11:15 am

Ciao Pan,
ce l'hai salvato il foglio di lavoro dinamico?
potresti inviarmelo come allegato?
volevo fare delle prove al fine di permetterne l'inserimento in un post.

Ho provato a generarne qualcuno di test con GeoGebra, ma non ho ancora capito come realizzare animazioni...

Grazie.

Saluti
Admin

panurgo · Messaggio da **panurgo** » sab nov 05, 2011 10:24 am

Come promesso ecco la dimostrazione del

Sezionamento di un quadrato in 21 quadratini

Questa è un'Applet Java creata con GeoGebra da www.geogebra.org - Java non risulta installato sul computer in uso - fare riferimento a www.java.com

R: "Dissezioni del quadrato" - 5. Per quali n è possibile dividere un quadrato in n quadra

R: "Dissezioni del quadrato" - 5. Per quali n è possibile dividere un quadrato in n quadra

Re: R: "Dissezioni del quadrato" - 5. Per quali n è possibile dividere un quadrato in n quadra

Re: R: "Dissezioni del quadrato" - 5. Per quali n è possibile dividere un quadrato in n quadra

Re: R: "Dissezioni del quadrato" - 5. Per quali n è possibile dividere un quadrato in n quadra