Gli orologi a tre cifre uguali
Moderatori: Gianfranco, Bruno
Questo forum è una sezione del PORTALE DI BASE CINQUE
-
Giorgio Dendi
- Nuovo utente

- Messaggi: 6
- Iscritto il: dom dic 30, 2007 9:00 pm
- Località: Trieste
- Contatta:
Gli orologi a tre cifre uguali
Ho acquistato alcuni orologi.
In ognuno di essi al posto dei numeri 1, 2, ... 12 ci sono delle formule, ciascuna delle quali formata da una sola delle cifre da 1 a 9, ripetuta esattamente tre volte.
Ad esempio, l'orologio con le cifre 9, ha al posto del 7 questa formula:
9 - radice di 9 + ,9periodico.
Al posto dell' 11, invece c'era la formula:
99 / 9.
Sono lecite tutte le operazioni che si sono viste in questi esempi e quelle più ovvie (quindi vale la virgola, il periodico, l'esponente, il fattoriale e il riunire due cifre per formare un'unico numero).
Assomiglia un po' al problema di ottenere 6 con tre numeri uguali (che avevo proposto qualche anno fa).
Ebbene, partendo da ciascun numero da 1 a 9 sono riuscito a completare tutti i 12 valori, meno che uno.
Quale?
PS: Ho proposto un problema simile su Brain Trainer (ex-Focus Giochi), per cui... non dite che l'ho copiato da lì.
In ognuno di essi al posto dei numeri 1, 2, ... 12 ci sono delle formule, ciascuna delle quali formata da una sola delle cifre da 1 a 9, ripetuta esattamente tre volte.
Ad esempio, l'orologio con le cifre 9, ha al posto del 7 questa formula:
9 - radice di 9 + ,9periodico.
Al posto dell' 11, invece c'era la formula:
99 / 9.
Sono lecite tutte le operazioni che si sono viste in questi esempi e quelle più ovvie (quindi vale la virgola, il periodico, l'esponente, il fattoriale e il riunire due cifre per formare un'unico numero).
Assomiglia un po' al problema di ottenere 6 con tre numeri uguali (che avevo proposto qualche anno fa).
Ebbene, partendo da ciascun numero da 1 a 9 sono riuscito a completare tutti i 12 valori, meno che uno.
Quale?
PS: Ho proposto un problema simile su Brain Trainer (ex-Focus Giochi), per cui... non dite che l'ho copiato da lì.
Ci sto lavorando un po' e li ho trovati quasi tutti, nel frattempo riporto alcune formule di carattere generale:
1 = x^(x-x)
2 = (x+x)/x
3 = radice(9)
6 = 3!
9 = radice(x*x)/,x
10 = radice(x*x)/,x
11 = xx/x
Inoltre esistono anche formule trasversali:
y=x: y=x+x-x
y=x±1: y=x±(x/x)
y=x±3: y=x±radice(x/,x)
y=x±6: y=x±radice(x/,x)!
y=9-x: y=x/,x-x
y=10-x: y=x/,x-x
SE&O
1 = x^(x-x)
2 = (x+x)/x
3 = radice(9)
6 = 3!
9 = radice(x*x)/,x
10 = radice(x*x)/,x
11 = xx/x
Inoltre esistono anche formule trasversali:
y=x: y=x+x-x
y=x±1: y=x±(x/x)
y=x±3: y=x±radice(x/,x)
y=x±6: y=x±radice(x/,x)!
y=9-x: y=x/,x-x
y=10-x: y=x/,x-x
SE&O
[Sergio] / $17$
Bel lavoro Antonio; ti è sfuggito che il 4 con i 7 si può ottenere con: 7-sqr(7/7)
Comunque, per non far torto agli operatori implementati nel Decimal Basic, direi:
ROUND(5+SQR(5)-.5) = 7
ROUND(7-SQR(7)-.7) = 4
ROUND(7-SQR(7)+.7) = 5
ROUND(7*SQR(7)-7) = 12
Comunque, per non far torto agli operatori implementati nel Decimal Basic, direi:
ROUND(5+SQR(5)-.5) = 7
ROUND(7-SQR(7)-.7) = 4
ROUND(7-SQR(7)+.7) = 5
ROUND(7*SQR(7)-7) = 12
_________________
$\text { }$ciao ciao
ciao
E' la somma che fa il totale (Totò)
$\text { }$ciao
E' la somma che fa il totale (Totò)
Il 12 con i 7:
$7 + \frac{log7}{log\sqr[5]{7}} = 12$
giustifico il 5 della radice, ritenendolo solo un operatore, altrimenti anche la radice quadrata non dovrebbe essere ammessa.
Se si volesse che gli indici delle radici non fossero sottintesi, il 2 della radice quadrata dovrebbe essere sempre visibile.
Insomma invoco la pari opportunità per tutte le radici ennesime, dovendo avere l'espressione di cui sopra pari dignità rispetto alla seguente:
$7 - \frac{log7}{log\sqr{7}} = 5$
Alla luce di quanto sopra, il 4 con i 7 si potrebbe esprimere anche così:
$7 - \frac{log7}{log\sqr[3]{7}} = 4$
Concludo, deducendo che l'unico numero non rappresentato dal nostro Dendi è stato il 7 non espresso con i 5, che però si può esprimere così:
$5 + \frac{log5}{log\sqr{5}} = 7$
oppure il 12 non espresso con i 7, non avendo egli voluto ammettere l'uso del 5 come indice della radice.
$7 + \frac{log7}{log\sqr[5]{7}} = 12$
giustifico il 5 della radice, ritenendolo solo un operatore, altrimenti anche la radice quadrata non dovrebbe essere ammessa.
Se si volesse che gli indici delle radici non fossero sottintesi, il 2 della radice quadrata dovrebbe essere sempre visibile.
Insomma invoco la pari opportunità per tutte le radici ennesime, dovendo avere l'espressione di cui sopra pari dignità rispetto alla seguente:
$7 - \frac{log7}{log\sqr{7}} = 5$
Alla luce di quanto sopra, il 4 con i 7 si potrebbe esprimere anche così:
$7 - \frac{log7}{log\sqr[3]{7}} = 4$
Concludo, deducendo che l'unico numero non rappresentato dal nostro Dendi è stato il 7 non espresso con i 5, che però si può esprimere così:
$5 + \frac{log5}{log\sqr{5}} = 7$
oppure il 12 non espresso con i 7, non avendo egli voluto ammettere l'uso del 5 come indice della radice.
_________________
$\text { }$ciao ciao
ciao
E' la somma che fa il totale (Totò)
$\text { }$ciao
E' la somma che fa il totale (Totò)
Che bel quiz e che bel lavoro avete già fatto 
Lascio solo una velocissima osservazione: tutta la
riga del 5 può essere omogeneamente ottenuta
anche così: a/(.a+.a), giusto per ricollegarmi al
primo post di Sergio
Mi chiedo se davvero non esista una combinazione
di tre 5 per ottenere 7 senza logaritmi
Un saluto a Giorgio anche da parte mia
Lascio solo una velocissima osservazione: tutta la
riga del 5 può essere omogeneamente ottenuta
anche così: a/(.a+.a), giusto per ricollegarmi al
primo post di Sergio
Mi chiedo se davvero non esista una combinazione
di tre 5 per ottenere 7 senza logaritmi
Un saluto a Giorgio anche da parte mia
Bruno
Ciao Bruno, auguri!
Per rispondere alla tua domanda direi che si potrebbe fare:
5 + 5^ + 5^ = 7
ed allo stesso modo si potrebbe ottenere il 5 dai 7:
7 - 7^ - 7^ = 5
se stabiliamo che la mancata indicazione dell'indice sottintende uno zero, così come è stato sottinteso uno zero alla notazione ,7 o ,7, o come si sottintende un 2 per la radice senza indice.
Se poi vogliamo allargare il campo, definendo delle nuove funzioni, o nuovi operatori, allora potremmo ottenere anche il 12 dai 7.
Si potrebbe definire ad esempio con INV una funzione che inverte le cifre e dunque:
INV(7+7+7) = 12
Nel linguaggio Basic, ad esempio viene implementata la funzione SWAP che scambia due elementi stringa fra loro, generando una stringa invertita, che può essere convertita in numero con la funzione VAL; esiste anche la possibilità (ad esempio in Quick Basic) di inventarsi una funzione a piacere, attribuendo alla stessa un nome, previo inserimento in libreria della relativa routine.
Comunque, con gli operatori Basic comuni ho già fatto qualche esempio in precedenza, utilizzando le funzioni di arrotondamento.
In sostanza, nel "mondo" Basic, come in altri, oltre le normali operazioni conosciute, se ne possono effettuare anche altre e diciamo che nel mondo Basic è possibile completare tutta la tabella.
Nel mondo "classico", per esprimere il 12 con i 7, ne occorrono 4.
Per rispondere alla tua domanda direi che si potrebbe fare:
5 + 5^ + 5^ = 7
ed allo stesso modo si potrebbe ottenere il 5 dai 7:
7 - 7^ - 7^ = 5
se stabiliamo che la mancata indicazione dell'indice sottintende uno zero, così come è stato sottinteso uno zero alla notazione ,7 o ,7, o come si sottintende un 2 per la radice senza indice.
Se poi vogliamo allargare il campo, definendo delle nuove funzioni, o nuovi operatori, allora potremmo ottenere anche il 12 dai 7.
Si potrebbe definire ad esempio con INV una funzione che inverte le cifre e dunque:
INV(7+7+7) = 12
Nel linguaggio Basic, ad esempio viene implementata la funzione SWAP che scambia due elementi stringa fra loro, generando una stringa invertita, che può essere convertita in numero con la funzione VAL; esiste anche la possibilità (ad esempio in Quick Basic) di inventarsi una funzione a piacere, attribuendo alla stessa un nome, previo inserimento in libreria della relativa routine.
Comunque, con gli operatori Basic comuni ho già fatto qualche esempio in precedenza, utilizzando le funzioni di arrotondamento.
In sostanza, nel "mondo" Basic, come in altri, oltre le normali operazioni conosciute, se ne possono effettuare anche altre e diciamo che nel mondo Basic è possibile completare tutta la tabella.
Nel mondo "classico", per esprimere il 12 con i 7, ne occorrono 4.
_________________
$\text { }$ciao ciao
ciao
E' la somma che fa il totale (Totò)
$\text { }$ciao
E' la somma che fa il totale (Totò)
Ma che razza di orologio avete??? Che segna mezzogiorno e mezzanotte come ai tempi dei babilonesi?? Suvvia mettiamoci quello che ci vuole - un bello zero - dopotutto sono numeri modulari no? E la riga dello zero diventa facilmente a*(a-a) ed ecco fatto 
Daniela
"L'essenza della libertà è la matematica"
"L'essenza della libertà è la matematica"
Re: Gli orologi a tre cifre uguali
La scoperta dell'esistenza di una funzione detta Primoriale (http://it.wikipedia.org/wiki/Primoriale) indicata con # mi ha infine permesso di trovare il modo di esprimere il 12 usando solo 3 volte il numero 7:
$\large \frac{7!}{7\sharp+7\sharp} = 12$
A breve la tabella completa.
$\large \frac{7!}{7\sharp+7\sharp} = 12$
A breve la tabella completa.
[Sergio] / $17$
Re: Gli orologi a tre cifre uguali
Sfrutando anche la funzione di Doppio Fattoriale (o Semifattoriale) indicata con !! possiamo esprimere il 7 con i 5 senza usare logaritmi o esponenti nulli sottointesi:
$\large 5+\frac{5\sharp}{5!!} = 7$
Ecco la tabella "definitiva"
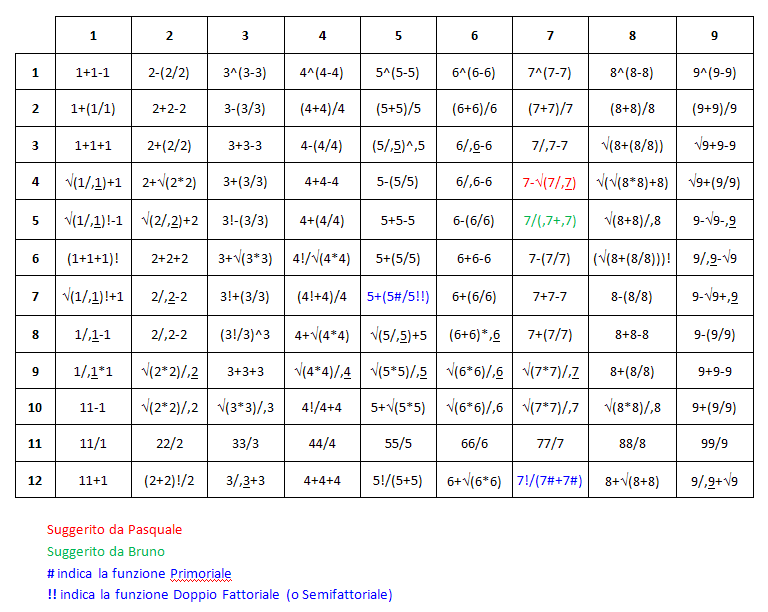
$\large 5+\frac{5\sharp}{5!!} = 7$
Ecco la tabella "definitiva"

[Sergio] / $17$
Re: Gli orologi a tre cifre uguali
Bravo Quelo, si trattava di trovare nuove vie, ma chissà se sono state esplorate tutte le possibilità con i normali operatori.
_________________
$\text { }$ciao ciao
ciao
E' la somma che fa il totale (Totò)
$\text { }$ciao
E' la somma che fa il totale (Totò)





