I quartetti di Thomas
Moderatori: Gianfranco, Bruno
Questo forum è una sezione del PORTALE DI BASE CINQUE
I quartetti di Thomas
Abbiamo una scacchiera nxn e 4xn pedine numerate.
Premesso che nelle caselle della diagonale principale non ci sono pedine, mettiamone 4 per colonna, 4 pedine col numero 1 nella prima colonna, 4 pedine col numero 2 nella seconda colonna, …, 4 pedine col numero n nell’ultima colonna. Invece in ogni riga devono esserci quattro pedine con numeri tutti diversi e non ci sono due righe uguali.
Diremo che la scacchiera è “poetica” se le somme dei quattro numeri di ogni fila danno sempre uno stesso numero k (la cosiddetta costante magica).
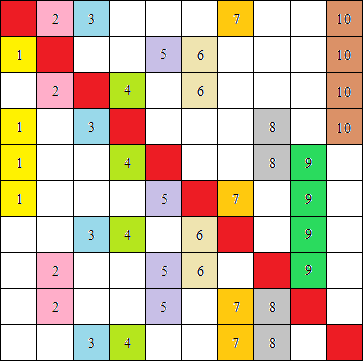
Un esempio con n=8 e k=18:
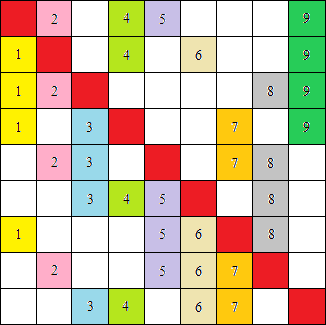
Problema 1 (facile). Trovare una scacchiera poetica per n=10
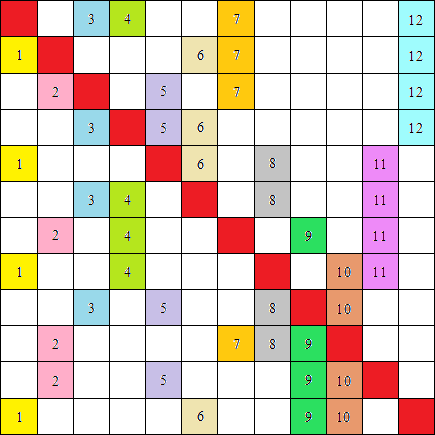
Problema 2 (meno facile). Trovare una scacchiera poetica per n=12
Premesso che nelle caselle della diagonale principale non ci sono pedine, mettiamone 4 per colonna, 4 pedine col numero 1 nella prima colonna, 4 pedine col numero 2 nella seconda colonna, …, 4 pedine col numero n nell’ultima colonna. Invece in ogni riga devono esserci quattro pedine con numeri tutti diversi e non ci sono due righe uguali.
Diremo che la scacchiera è “poetica” se le somme dei quattro numeri di ogni fila danno sempre uno stesso numero k (la cosiddetta costante magica).
Un esempio con n=8 e k=18:
Problema 1 (facile). Trovare una scacchiera poetica per n=10
Problema 2 (meno facile). Trovare una scacchiera poetica per n=12
-
Maurizio59
- Livello 4

- Messaggi: 127
- Iscritto il: mar lug 26, 2022 9:02 am
Re: I quartetti di Thomas
Bravo Maurizio59, il Problema 1 è stato risolto, aspetto per il Problema 2.
-
Maurizio59
- Livello 4

- Messaggi: 127
- Iscritto il: mar lug 26, 2022 9:02 am
Re: I quartetti di Thomas
Ottimo, direi, con questo abbiamo chiuso l'argomento del titolo, salvo eventuali commenti extra.
Sto preparando altre due cosette coi quartetti, il tempo di controllare e scrivere poi arrivo.
Sto preparando altre due cosette coi quartetti, il tempo di controllare e scrivere poi arrivo.
Re: I quartetti di Thomas
Per trovare rapidamente una soluzione si può usare il seguente metodo, che chiamerò "riempimento a farfalla" (per n>=10)
Si tratta in sostanza di disegnare una schema a farfalla partendo da 1,2,n-1,n fino a (n/2)-1,(n/2),(n/2)+1,(n/2)+2
Per le prime quattro righe teniamo fermi gli estremi e stringiamo al centro: 1,3,n-2,n ; 1,4,n-3,n ; 1,5,n-4,n
A questo punto stringiamo gli estremi e ricominciamo.
Vediamo n=10 come esempio, in quanto il procedimento è lineare
n=10; k=22
Sarà quindi sufficiente riorganizzare le righe per non avere numeri sulla diagonale
Per n>10 le scalette al centro vanno rimodulate per evitare di avere più di 4 numeri in colonna
n=12; k=26
n=14; k=30
n=16; k=34
Si tratta in sostanza di disegnare una schema a farfalla partendo da 1,2,n-1,n fino a (n/2)-1,(n/2),(n/2)+1,(n/2)+2
Per le prime quattro righe teniamo fermi gli estremi e stringiamo al centro: 1,3,n-2,n ; 1,4,n-3,n ; 1,5,n-4,n
A questo punto stringiamo gli estremi e ricominciamo.
Vediamo n=10 come esempio, in quanto il procedimento è lineare
n=10; k=22
Codice: Seleziona tutto
1 2 9 10
1 3 8 10
1 4 7 10
1 5 6 10
2 3 8 9
2 4 7 9
2 5 6 9
3 4 7 8
3 5 6 8
4 5 6 7
Per n>10 le scalette al centro vanno rimodulate per evitare di avere più di 4 numeri in colonna
n=12; k=26
Codice: Seleziona tutto
1 2 11 12
1 3 10 12
1 4 9 12
1 5 8 12
2 4 9 11
2 5 8 11
2 6 7 11
3 4 9 10
3 5 8 10
3 6 7 10
4 6 7 9
5 6 7 8
Codice: Seleziona tutto
1 2 13 14
1 3 12 14
1 4 11 14
1 5 10 14
2 4 11 13
2 5 10 13
2 6 9 13
3 5 10 12
3 6 9 12
3 7 8 12
4 6 9 11
4 7 8 11
5 7 8 10
6 7 8 9
Codice: Seleziona tutto
1 2 15 16
1 3 14 16
1 4 13 16
1 5 12 16
2 6 11 15
2 7 10 15
2 5 12 15
3 6 11 14
3 7 10 14
3 8 9 14
4 5 12 13
4 6 11 13
4 7 10 13
5 8 9 12
6 8 9 11
7 8 9 10
[Sergio] / $17$
-
Maurizio59
- Livello 4

- Messaggi: 127
- Iscritto il: mar lug 26, 2022 9:02 am
Re: I quartetti di Thomas
Re: I quartetti di Thomas
Con n dispari c'è un elemento centrale che disturba la simmetria
Credo che la soluzione per n=9 sia unica, perché esistono solo 4 combinazioni di 4 cifre che contengono il 5 e la cui somma è 20
Per n>9 non c'è un'approccio generalizzato. Lo riempimento a farfalla ci viene incontro, ma bisogna sacrificare la simmetria
n = 9; k = 20
n = 11; k = 24
n = 13; k = 28
Credo che la soluzione per n=9 sia unica, perché esistono solo 4 combinazioni di 4 cifre che contengono il 5 e la cui somma è 20
Per n>9 non c'è un'approccio generalizzato. Lo riempimento a farfalla ci viene incontro, ma bisogna sacrificare la simmetria
n = 9; k = 20
Codice: Seleziona tutto
1 2 8 9 X 3 4 6 7
1 3 7 9 X 3 4 5 8
1 4 7 8 1 2 X 8 9
1 5 6 8 1 3 X 7 9
2 3 6 9 1 4 X 7 8
2 4 5 9 2 4 5 X 9
2 5 6 7 2 3 6 X 9
3 4 5 8 2 5 6 7 X
3 4 6 7 1 5 6 8 X
Codice: Seleziona tutto
1 2 10 11 X 4 5 6 9
1 3 9 11 X 3 6 7 8
1 4 8 11 1 2 X 10 11
1 5 7 11 1 3 X 9 11
2 4 8 10 1 4 X 8 11
2 5 7 10 1 5 X 7 11
2 6 7 9 3 5 6 X 10
3 5 6 10 2 6 7 X 9
3 4 8 9 2 4 8 X 10
3 6 7 8 3 4 8 9 X
4 5 6 9 2 5 7 10 X
Codice: Seleziona tutto
1 2 12 13 X 5 6 8 9
1 3 11 13 X 3 4 10 11
1 4 10 13 1 2 X 12 13
1 6 9 12 1 3 X 11 13
2 6 7 13 1 4 X 10 13
2 6 8 12 4 5 X 9 10
2 7 8 11 1 6 X 9 12
3 4 10 11 2 6 7 X 13
3 5 9 11 2 6 8 X 12
3 7 8 10 3 5 9 X 11
4 5 7 12 3 7 8 10 X
4 5 9 10 2 7 8 11 X
5 6 8 9 4 5 7 12 X
[Sergio] / $17$