panurgo ha scritto: ↑ven ott 18, 2019 4:03 pm
La vedo dura...
Infatti, dalla figura seguente
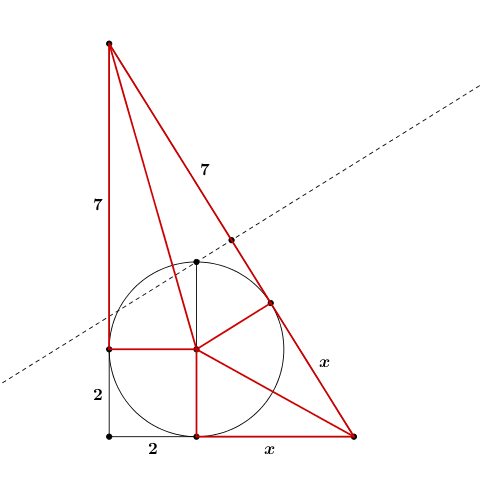
- LIFAM03.1_480x480.png (20.95 KiB) Visto 4150 volte
ricaviamo l’equazione $\left(x+7\right)^2=\left(x+2\right)^2+9^2$ che, con facile algebra, fornisce $x=3,6$.
Se l’intersezione della perpendicolare è veramente il punto medio del segmento allora i segmenti evidenziati in figura
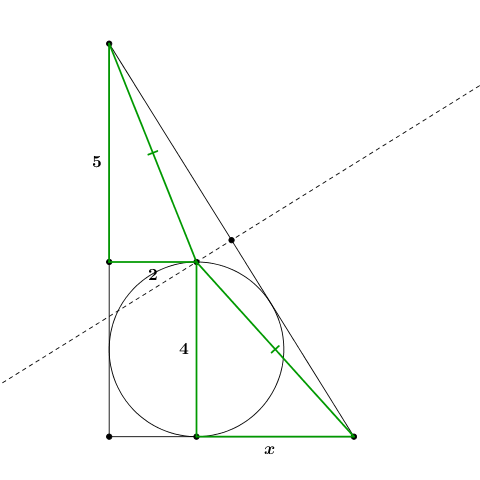
- LIFAM03.2_480x480.png (18.95 KiB) Visto 4150 volte
devono essere congruenti e deve valere l’equazione $x^2+4^2=5^2+2^2$ dalla quale ricaviamo immediatemente $x=\sqrt{13}$.
Ma $\sqrt{13}\neq3,6$: come la mettiamo?
Se consideriamo una circonferenza inscritta di raggio pari a $2$ possiamo vedere quanto deve essere lungo il cateto maggiore perché il teorema sia vero
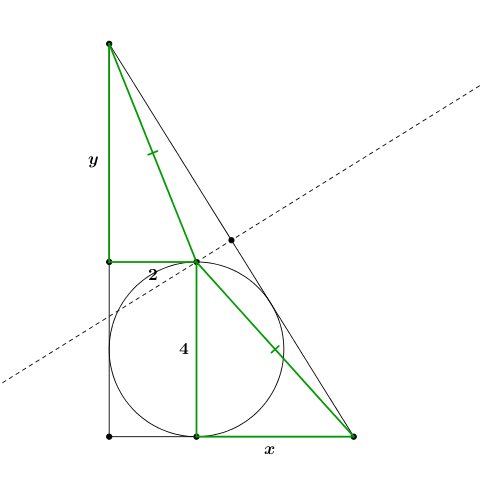
- LIFAM03.3_480x480.png (19.21 KiB) Visto 4150 volte
Sostituito il $5$ con $y$ abbiamo
$\displaystyle\left\{\begin{array}{lC} \left(x+y+2\right)^2=\left(x+2\right)^2+(y+4)^2 \\ x^2+4^2=y^2+2^2 \end{array}\right.$
ovvero
$\displaystyle\left\{\begin{array}{lC} x^2 y^2=4y^2+32y+64 \\ x^2=y^2-12 \end{array}\right.$
da cui ricaviamo l’equazione di quarto grado
$\displaystyle y^4-16y^2-32y-64=0$
che diamo in pasto a
alpha: l’equazione ha due radici reali, una negativa e una positiva (quella che ci interessa!)
$y=\sqrt {\frac23 \left(4-\frac8{\sqrt[3]{9\sqrt{41}-53}}+\sqrt[3]{9\sqrt{41}-53}\right)}-\sqrt{8-\frac23 \left(4-\frac8{\sqrt[3]{9\sqrt{41}-53}}+\sqrt[3]{9\sqrt{41}-53}\right) +4\sqrt{\frac6{4-\frac8{\sqrt[3]{9\sqrt{41}-53}}+\sqrt[3]{9\sqrt{41}-53}}}}$
ovvero $y=4,9967\ldots$