Pagina 1 di 1
Sulla lavagna...cancella e scrivi (1)
Inviato: mer set 25, 2019 9:48 pm
da Gianfranco
Questo problemino è anche nella home del sito.
Problema 1.
Sulla lavagna sono scritti i numeri da 1 a 10.
Scegli due numeri a caso, $a$, $b$, cancellali e scrivi al loro posto il numero $a+b+ab$.
Ora ci sono 9 numeri sulla lavagna.
Ripeti la procedura: scegli due numeri a caso, cancellali e scrivi sulla lavagna il numero dato dalla loro somma più il loro prodotto.
Ora ci sono 8 numeri sulla lavagna.
Ripeti la procedura fino a quando sulla lavagna c'è un solo numero.
Che numero è?
---
Problema 2. (variazione sul tema)
Al posto di $a$, $b$, scrivi $\sqrt{a^2+b^2}$.
Che numero ottieni alla fine?
Re: Sulla lavagna...cancella e scrivi (1)
Inviato: gio set 26, 2019 12:35 am
da Pasquale
Nel 1° caso, direi 39.916.799 :
Codice: Seleziona tutto
DIM n(10)
FOR m=1 TO 10
LET n(m)=m
NEXT M
RANDOMIZE
FOR m=1 TO 9
10
LET a=1+INT(RND*10)
IF n(a)=0 THEN GOTO 10
20
LET b=1+INT(RND*10)
IF n(b)=0 OR b=a THEN GOTO 20
LET c=n(a)+n(b)+n(a)*n(b)
LET n(a)=c
LET n(b)=0
NEXT m
FOR m=1 TO 10
IF n(m)>0 THEN PRINT n(m)
NEXT M
END
Nel 2°caso 19,621416870.......... :
Codice: Seleziona tutto
DIM n(10)
FOR m=1 TO 10
LET n(m)=m
NEXT M
RANDOMIZE
FOR m=1 TO 9
10
LET a=1+INT(RND*10)
IF n(a)=0 THEN GOTO 10
20
LET b=1+INT(RND*10)
IF n(b)=0 OR b=a THEN GOTO 20
LET c=SQR(n(a)^2+n(b)^2)
LET n(a)=c
LET n(b)=0
NEXT m
FOR m=1 TO 10
IF n(m)>0 THEN PRINT n(m)
NEXT M
END
Re: Sulla lavagna...cancella e scrivi (1)
Inviato: gio set 26, 2019 9:33 am
da Gianfranco
Pasquale, perfetto!
Due programmi scritti bene!
Nel primo caso il risultato è $11!-1$ e nel secondo $\sqrt{385}$ (somma dei quadrati dei numeri da 1 a 10).
Come hai certamente notato, il risultato non dipende dall'ordine di estrazione dei numeri quindi è un invariante.
Come si può dimostrare senza usare il computer?
Re: Sulla lavagna...cancella e scrivi (1)
Inviato: gio set 26, 2019 11:48 am
da panurgo
Consideriamo tre numeri $a$, $b$ e $c$ e applichiamo l’algoritmo in questo ordine:
primo passo
$\displaystyle \left\{a,\,b,\,c\right\}\quad\to\quad\left\{\left(a+b+ab\right),\,c\right\}$
e il primo dei due numeri rimasti e simmetrico rispetto allo scambio tra $a$ e $b$;
secondo passo
$\displaystyle \left\{\left(a+b+ab\right),\,c\right\}\quad\to\quad\left\{\left(a+b+ab\right)+c+\left(a+b+ab\right)c\right\} =\left\{\left(a+b+c+ab+ac+bc+abc\right)\right\} $
il numero finale è simmetrico rispetto allo scambio di $a$, $b$ e $c$.
Un quarto numero, $d$, viene aggiunto come tale (grado 1) e moltiplicato per gli altri (grado 2), per il prodotto degli altri due a due (grado 3) ed infine per il prodotto degli altri tre (grado 4): il risultato rimane simmetrico rispetto allo scambio tra numeri.
Un quinto numero... ecc.
Non ho verve di formalizzarlo più di così, ma mi sembra abbastanza evidente.
Re: Sulla lavagna...cancella e scrivi (1)
Inviato: gio set 26, 2019 7:05 pm
da panurgo
Per il problema due ho una dimostrazione visuale
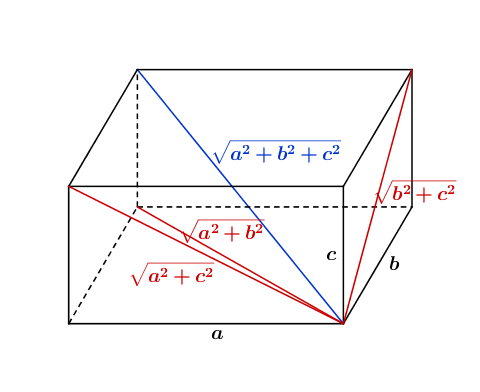
- SL-C&S.02.png (21 KiB) Visto 5691 volte
Evidentemente il risultato finale non dipende dall'ordine con il quale scegliamo gli spigoli da seguire (mi dispiace: ho provato a fare il disegno con più di tre numeri ma non ci sono riuscito...

)
Re: Sulla lavagna...cancella e scrivi (1)
Inviato: ven set 27, 2019 12:24 am
da Pasquale
Ho provato a dare una risposta a quanto richiesto da Gianfranco, ma al momento non ho individuato una strada da seguire.
Per quanto riguarda invece la routine, così come concepita, ho pensato che in fondo l'esatto risultato prodotto dalla stessa potrebbe essere dovuto ad una fortunata casualità.
Quindi, per aumentare la validità dell'uso della routine, ho apportato alla stessa una piccola modifica, reiterando il procedimento 10.000 volte, sommandone i risultati ed estraendone la media, nel tentativo di diminuire i dubbi sulla possibilità di un risultato scarsamente accettabile, perché semplicemente fortunato.
Inoltre, la routine così integrata può essere avviata più volte, oppure la suddetta reiterazione può essere ulteriormente aumentata, optando per la doppia precisione di cui dispone Decimal Basic.
In sostanza, se il risultato non sarà mai diverso, si può pur concludere che sia molto probabilmente esatto, anche se potrebbe essere sempre considerato non certissimo, ma con scarsa probabilità, in linea di principio, che possa essere molto diverso.
Codice: Seleziona tutto
DIM n(10)
LET tot=0
FOR p=1 TO 10000
FOR m=1 TO 10
LET n(m)=m
NEXT M
RANDOMIZE
FOR m=1 TO 9
10
LET a=1+INT(RND*10)
IF n(a)=0 THEN GOTO 10
20
LET b=1+INT(RND*10)
IF n(b)=0 OR b=a THEN GOTO 20
LET c=n(a)+n(b)+n(a)*n(b)
LET n(a)=c
LET n(b)=0
NEXT m
FOR m=1 TO 10
IF n(m)>0 THEN LET tot=tot+n(m)
NEXT M
NEXT P
PRINT tot/10000
END
Re: Sulla lavagna...cancella e scrivi (1)
Inviato: ven set 27, 2019 12:53 pm
da panurgo
Torno alla carica con il primo problema.
Abbiamo visto che il risultato non dipende dall’ordine con cui scegliamo i numeri quindi possiamo procedere in ordine crescente:
con $\left\{1\right\}$ abbiamo $1=2!-1$;
con $\left\{1,\,2\right\}$ abbiamo $\left(2!-1\right)+2+2\cdot \left(2!-1\right) =2!+2\cdot 2!-1=3\cdot 2!-1=3!-1$;
con $\left\{1,\,2,\,3\right\}$ abbiamo $\left(3!-1\right)+3+3\cdot \left(3!-1\right) =3!+3\cdot 2!-1=4\cdot 3!-1=4!-1$;
con $\left\{1,\,2,\,3,\,4\right\}$ abb...
Re: Sulla lavagna...cancella e scrivi (1)
Inviato: ven set 27, 2019 2:33 pm
da Gianfranco
@Pasquale,
ti ringrazio nuovamente per i programmini che sono chiari, efficienti, concisi.
Credo però che l'ultimo, quello con la ripetizione delle prove, in realtà non aggiunga molto perché basta eseguire poche volte i programmi singoli per iniziare a sospettare che i risultati siano sempre gli stessi.
E questo fatto spinege a indagare sulla struttura dell'algoritmo per dimostrare matematicamente l'invarianza del risultato.
@panurgo,
bella la dimostrazione visuale. In pratica è come calcolare la diagonale di un parallelepipedo rettangolo a 10 dimensioni.
Interessanti anche le argomentazioni sull'altro problema, grazie.