Franco, non posso rispondere a questa domanda, perché ho impostato una routine diversa che tiene conto di 5.000.000 di alfa, scelti anch'essi a caso fra 0 e 180°. Ho pensato che 3 alfa soltanto fossero pochi.
Chiaramente il dato che ha partorito la routine (lanciata più volte) è approssimato, ma l'approssimazione alla 3^ cifra decimale è risultata stabile.
Tuttavia, poiché gli angoli rispetto ai quali ho scelto a caso i punti P e Q sono anch'essi casuali, con misure anche decimali, provo a studiare qualche altra routine che distribuisca la casualità solo sulla posizione dei P e Q, in pari quantità per ciascuno dei 180 alfa, presi di grado in grado fra i 180°di cui trattiamo.
Dovrebbe venir fuori un risultato più vicino alla precisione, comunque da confrontare con il precedente 0,826.
Il fatto che abbia trattato con casualità anche l'ampiezza di alfa è dovuto ad una semplificazione automatica rispetto al tipo di impostazione della routine (segue chiarimento per chi fosse interessato):
.
.
- Triangolo isoscele.JPG (11.27 KiB) Visto 5862 volte
.
.
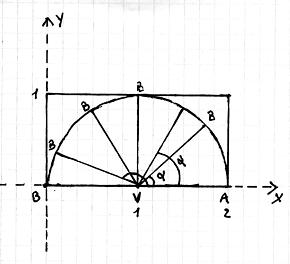
Con riferimento al piano cartesiano di cui al disegno , che rappresenta i lati del triangolo in questione, ho mantenuto fisso il lato VA di misura 1, su cui scegliere in modo casuale un punto P, ed ho variato l’angolo alfa nell’ambito dei 180°, stabilendo in tal modo la posizione del lato VB, su cui scegliere un punto Q, anche questo in modo casuale. La routine calcola conseguentemente ogni volta la distanza PQ.
In particolare, nella routine l’operazione di scelta casuale riguarda la posizione del punto Q nell’ambito dell'area del rettangolo che contiene il semicerchio e conseguentemente viene definita automaticamente anche l’apertura dell’angolo alfa.
Se in base alla posizione di Q la misura di VQ non supera l’unità, la posizione viene ritenuta valida e quindi, una volta scelta casualmente anche la posizione del punto P , si misura PQ.
L’operazione viene ripetuta 5.000.000 di volte e tutte le misure di PQ vengono ogni volta sommate.
Dividendo infine per 5000.000 la somma totale, ottengo un risultato medio, che quanto sia aderente a quanto cercato è ancora da valutare.
LET cont=0
LET y1=0
LET PQ=0
RANDOMIZE
do
LET x2=INT(1000*(RND*2))/1000 !'ascissa casuale del punto Q
LET y2=INT(1000*RND)/1000 !'ordinata casuale del punto Q
LET DQV=SQR((1-x2)^2+(y2)^2) !'distanza del punto Q dal vertice
IF DQV<=1 THEN
LET cont=cont+1
LET x1=INT((1+RND)*1000)/1000 !'ascissa casuale del punto P
LET PQc=SQR((x1-x2)^2+(y2)^2)!'misura PQ casuale
LET PQ=PQ+PQc
IF cont=5000000 THEN EXIT DO
END IF
LOOP
PRINT "PQ medio =";PQ/5000000
END
 Esprimere in funzione di α la distanza media M(α) fra P e Q.
Esprimere in funzione di α la distanza media M(α) fra P e Q. Calcolare M(α) per α = π/3, α = π/2, α = 2π/3
Calcolare M(α) per α = π/3, α = π/2, α = 2π/3 Calcolare il limite di M(α) per α che tende a 0 e per α che tende a π.
Calcolare il limite di M(α) per α che tende a 0 e per α che tende a π.