Pagina 1 di 1
Sottrazioni in ambo le direzioni
Inviato: lun apr 29, 2019 7:55 am
da giobimbo
Dato un poligono di n lati (e quindi anche n vertici) assegniamo a ogni vertice un numero da 1 a n (non in questo ordine però…), a ogni vertice un numero diverso. Duplichiamo tale poligono ottenendo quelli che senza tanta fantasia chiamiamo Poligono1 e Poligono2.
Sia l il lato di estremi a e b, l=(a,b); diamogli un valore che, come nella teoria dei grafi chiamiamo “peso”, scrivendo $peso_{(a,b)}$ e poniamo:
$peso1_{(a,b)}$=differenza modulo (n+1) di a e b per Poligono1
$peso2_{(a,b)}$=differenza modulo (n+1) di b e a per Poligono2
ovvero
$peso1_{(a,b)}$=a-b (mod n+1)
$peso2_{(a,b)}$=b-a (mod n+1)
Un esempio con n=4 e quindi differenze modulo 5:

- base5 Poligono1 e Poligono2.png (9.42 KiB) Visto 4053 volte
Siccome disegnare poligoni con numeri sui vertici e sui lati è abbastanza complicato, alla figura si può sostituire una sequenza ordinata (i vertici letti in senso orario) per cui l’esempio diventerebbe:
Poligono1=Poligono2=(1, 3, 4, 2)
e aggiungendo in rosso le differenze modulari:
Poligono1=(1,
3, 3,
4, 4,
2, 2,
1)
Poligono2=(1,
2, 3,
1, 4,
3, 2,
4).
Come si vede i numeri in rosso sono tutti diversi.
Problema: dato un poligono di 12 lati numerare i suoi vertici in modo che Poligono1 e Poligono2 abbiano pesi (cioè differenze modulo 13, cioè numeri in rosso) tutti diversi.
Re: Sottrazioni in ambo le direzioni
Inviato: dom mag 19, 2019 3:56 am
da Pasquale
Questo, considerato l'antico mio difetto di una scarsa propensione alla sinteticità, non l'ho capito.
Re: Sottrazioni in ambo le direzioni
Inviato: mar mag 21, 2019 9:52 am
da giobimbo
Allora: i vertici del poligono a 4 lati sono numerati in sequenza 1, 3, 4, 2 come si vede anche in figura, con la convenzione che, procedendo in senso orario, dopo il vertice 2 si ricomincia dal vertice 1. Facciamo le sottrazioni (mod 5)
1 - 3 = 3
3 - 4 = 4
4 - 2 = 2
2 - 1 = 1
Questi sono i pesi, cioè i valori assegnati ai lati del Poligono1, in figura a sinistra.
Per il Poligono2 le sottrazioni si fanno procedendo in senso antiorario, quindi leggendo i vertici al contrario, con la convenzione che dopo il vertice 1 si ricomincia dal vertice 2, allora le sottrazioni (mod 5) sono
1 - 2 = 4
2 - 4 = 3
4 - 3 = 1
3 - 1 = 2
Questi sono i pesi, cioè i valori assegnati ai lati del Poligono2, in figura a destra.
Le sottrazioni in senso orario (i numeri in rosso) sono tutti diversi (vedi Poligono1), lo stesso per le sottrazioni in senso antiorario (vedi Poligono2). Ora si tratta di numerare un dodecagono coi numeri da 1 a 12 in modo da ottenere i risultati delle sottrazioni (mod 13) tutti diversi in senso orario e tutti diversi anche procedendo in senso antiorario. Spero di essere stato abbastanza chiaro, ma se ci sono dei dubbi
@ Tutti
basta chiedere.
Re: Sottrazioni in ambo le direzioni
Inviato: mer mag 22, 2019 11:22 am
da Gianfranco
Per la mia povera mente, il caso con 12 lati ha una potenza combinatoria inaffrontabile, comunque la prima delle migliaia di soluzioni in ordine lessicografico dovrebbe essere questa.
1 [12] 2 [11] 4 [1] 3 [6] 10 [2] 8 [10] 11 [4] 7 [8] 12 [7] 5 [9] 9 [3] 6 [5] 1
1 [1] 2 [2] 4 [12] 3 [7] 10 [11] 8 [3] 11 [9] 7 [5] 12 [6] 5 [4] 9 [10] 6 [8] 1
dove i pesi dei lati sono in parentesi quadre anziché in rosso.
Più dominabile invece il caso con 6 lati.
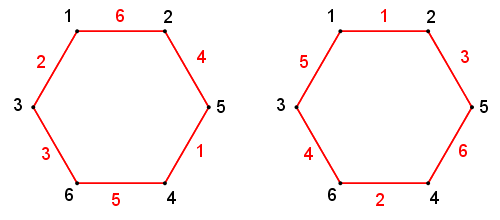
- giobimbo_sottraz_modulo.PNG (9.63 KiB) Visto 4003 volte
Ho una domanda: perché il problema non ha soluzioni per n dispari?
(dove n è il numero dei lati del poligono)
Re: Sottrazioni in ambo le direzioni
Inviato: ven mag 24, 2019 8:33 am
da giobimbo
Molto bene, bravo Gianfranco per la tua soluzione! Sono contento che tu abbia terminato il periodo sabbatico e sia tornato a dedicarti con impegno al sito. Per la tua domanda ti rispondo in privato (in giornata, spero, sono lento nello scrivere) usando l’elenco degli iscritti, giusto? Non voglio togliere il piacere dell’investigazione a chi cerca soluzioni per valori di n qualsiasi.
Alcune considerazioni: mi sembrava esagerato ricorrere a un programma per trovare la soluzione, come talvolta fa anche Pasquale, dopotutto si tratta solo di un gioco, poi ho capito che anch’io quando procedo per tentativi faccio lo stesso lavoro di un programma.
Vero è che un programma, come un treno, ti porta a destinazione ma ti perdi i dettagli del paesaggio che procedendo a piedi uno avrebbe notato. E poi vien da dire che non sono stato io a trovare la soluzione ma il programma…
Ma il creare il programma fa parte della sfida, inoltre il trovare delle soluzioni aiuta a capire il meccanismo, ad approfondire lo studio del problema in generale. Una soddisfazione incredibile.