Pagina 1 di 1
A rapporto :)
Inviato: lun dic 03, 2018 5:46 pm
da Bruno
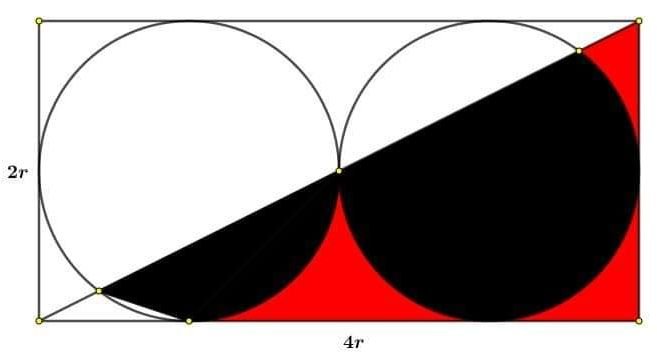
- 1.jpg (16.14 KiB) Visto 5926 volte
Qual è il rapporto fra l'area rossa e l'area nera?
Re: A rapporto :)
Inviato: mar dic 04, 2018 5:43 pm
da panurgo
Sono stupito di non essere stato anticipato in questo: procedendo spannometricamente, more Delfi, e trascurando l'insidioso triangolino in basso a sinistra il rapporto è approssimativamente uguale metà dell'area di due quadrati meno metà dell'area di due cerchi diviso per metà dell'area di due cerchi
$\displaystyle \frac{Q - C}C=\frac Q C-1=\frac4\pi-1=0,27\ldots$
Se invece vogliamo essere un po' più accurati dobbiamo togliere l'area del triangolino un po' dal quadrato e un po' dal cerchio
$\displaystyle \frac{Q - C - t + s}{C - s}=\frac {Q - t}{C - s}-1$
dove $t$ è l'area totale del triangolino e $s$ è l'area del segmento circolare tagliato dal cerchio nel triangolino stesso.
Per far ciò fissiamo un sistema di assi cartesiani ortogonali, centrato nell'angolo inferiore sinistro della figura e con unità di misura pari a $r$: l'equazione della retta passante per la diagonale è $x-2y=0$ mentre quella della circonferenza è $\left(x-1\right)^2+\left(y-1\right)^2=1$ da cui, con pochi passaggi di facile algebra si ricava un'equazione di secondo grado in $y$ le cui radici sono $1$, corrispondente all'intersezione in $\left(2;1\right)$, e $\frac15$, corrispondente all'intersezione (che ci interessa) in $\left(\frac25;\frac15\right)$.
Vediamo subito che $t=\frac1{10}$ e che la base del segmento circolare vale $\frac1{\sqrt5}$: l’area del segmento circolare vale
$\displaystyle s=\frac{\vartheta - \sin\vartheta}2=\arcsin{\frac1{\sqrt{10}}}-\frac3{10}=0,021\ldots$
per cui
$\displaystyle \frac{Q - C - t + s}{C - s}=\frac {Q - t}{C - s}-1=\frac {3,9}{\pi - 0,021\ldots}-1=0,2500\ldots$
La spannometria ci ha dato un'approssimazione molto buona: una sovrastima dell'$ 8\%$.
Re: A rapporto :)
Inviato: mar dic 04, 2018 10:01 pm
da delfo52
chiamato in causa, espongo la mia "soluzione" approssimativa.
L'area nera è appena un pizzico meno dell'area di un cerchio. Invece 3,14159..., prendiamo 3,1 (che è semplice da maneggiare)
L'area nera , se anche tutto lo spicchio in alto a destra fosse rosso, sarebbe 4 meno pigreco = 0,8584
uno spicchio singolo vale quindi 0,214...
al totale dei quattro spicchi (0,8584 ne devo togliere un po' meno di mezzo spicchio), per cui tolgo 0,1
L'area rossa viene perciò 0,7584 (avere più decimali non è un problema, anzi serve per fare la divisione senza aggiungere degli zeri)
0,7584 / 0,31 = 2,4464
Re: A rapporto :)
Inviato: mer dic 05, 2018 12:11 pm
da Bruno
Ottimo, Guido

Enrico, se quel 2,4464 è in realtà 0,24464, il tuo metodo è davvero mirabile

Re: A rapporto :)
Inviato: mer dic 05, 2018 4:30 pm
da delfo52
le virgole mi sono scivolate in qua e in là… e anche il colore rosso è diventato nero una volta. Ma credo che si capisca
Re: A rapporto :)
Inviato: mer dic 05, 2018 6:08 pm
da Bruno
Grande Enrico

Re: A rapporto :)
Inviato: mer dic 05, 2018 8:48 pm
da panurgo
Questa mi è venuta solo dopo: se siamo veramente spannometrici, trascuriamo il triangolino e usiamo l'approssimazione biblica di $\pi$ ($3$!) otteniamo un rapporto di $\frac14$ che differisce dal valore esatto di meno di $6\times10^{-5}$...

Re: A rapporto :)
Inviato: mer dic 05, 2018 11:14 pm
da Pasquale
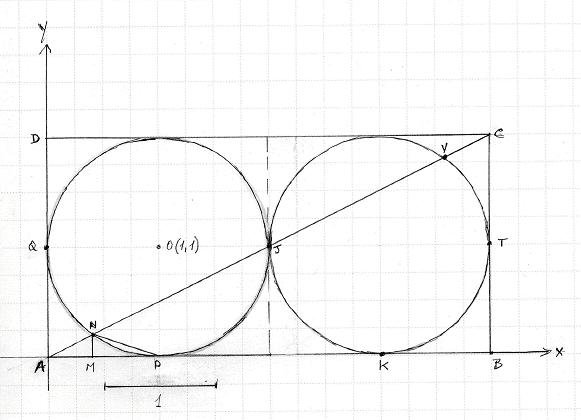
- Cerchi.JPG (35.26 KiB) Visto 5859 volte
Già tutto è stato scritto e non farò calcoli, avendo in questo periodo poco tempo a disposizione per lo svago.
Vorrei solo aggiungere qualcosa sulla precisione, a parte la presenza del pigreco (chissà se il rapporto da effettuare fra rosso e nero non vada a diminuire l'influenza dello stesso circa l'imprecisione del calcolo).
Semplificando il procedimento con r=1, discende che l'area di ogni cerchio vale $\pi$, che come già rilevato rappresenta approssimativamente l'area colorata in nero, alla quale per la precisione occorre sottrarre il segmentino circolare, che vedrei come differenza fra l'area del triangolo MNP e l'area MNP sottesa all'arco NP, da individuare col calcolo integrale (Integ) nell'intervallo fra M e P dell'asse delle x, premesso che una volta individuate le cooordinate del punto N(2/5,1/5), come già fatto da Panurgo, possiamo considerare note le aree dei triangoli AMN e MNP, che risulteranno utili per individuare anche altre misure che interessano.
Infatti, l'area colorata in rosso possiamo considerarla come somma delle aree $KBT= \frac{(4-\pi)}{4}$, dell'area PJK doppia di KBT e dell'area CVT = ANQ = APQ - AMN - Integ
Altra possibilità di calcolo approssimato potrebbe essere affidata al Decimal Basic con una routine che, attribuendo valori casuali ad x ed y, nell'ambito di intervalli predefiniti in quanto coordinate di punti ricadenti nell'area interessata del rettangolo 4x2, conteggiasse quanti appartenenti all'area colorata in rosso, quanti all'area colorata in nero, quanti a nessuna delle due. La routine terminerebbe col calcolo del rapporto di cui trattasi (ponendo cioè in rapporto il numero dei punti caduti casualmente nell'area rossa con quelli finiti nell'area nera) . Sarebbe interessante confrontare i risultati ottenuti con i due procedimenti, per valutare l'attendibilità del procedimento descritto, dipendente in particolar modo dalla quantità dei punti "sparati" casualmente nell'area interessata: mi riservo un esempio semplificato appena possibile, dal titolo "Esempio semplificato".
