Vediamo se è possibile renderla un po’ più rigorosa.
Premesso che il quadrato ha lato unitario, osserviamo che:
1.un semicerchio deve essere quanto più possibile vicino ad un lato in modo da lasciare spazio agli altri semicerchi.
2.quando un semicerchio è tangente ad un lato con la base occupa meno spazio dello stesso semicerchio tangente al lato con la semicirconferenza
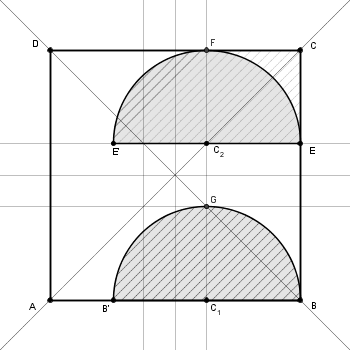
- panurgo_SC&Q013b.png (22.88 KiB) Visto 6579 volte
3.quando un semicerchio è tangente al lato con la semicirconferenza, il suo centro giace su una delle rette $x\,=\,r$, $x\,=\,1\,-\,r$, $y\,=\,r$ o $y\,=\,1\,-\,r$
4.quando il semicerchio è tangente con la semicirconferenza a due lati (consecutivi) il suo centro giace su due di tali rette e quindi su una diagonale del quadrato
5.quando un semicerchio è tangente con la base alla semicirconferenza di un altro semicerchio, l'altezza raggiunta è minima quando il punto di tangenza è il centro del semicerchio (che giace su una delle rette)
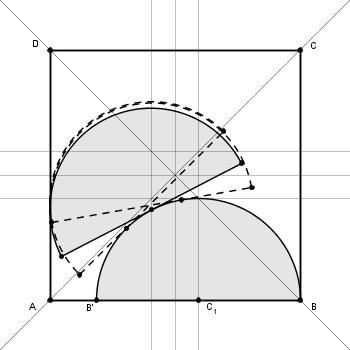
- panurgo_SC&Q014b.png (15.52 KiB) Visto 6579 volte
questo perché cambiando punto di tangenza il centro del semicerchio si alza e la semicirconferenza dista sempre $r$ dal centro stesso.
Di conseguenza, il massimo che si può ottenere con un semicerchio tangente con la base e gli altri due con la semicirconferenza è quello in figura (con $r\,=\,\frac5{13}$)
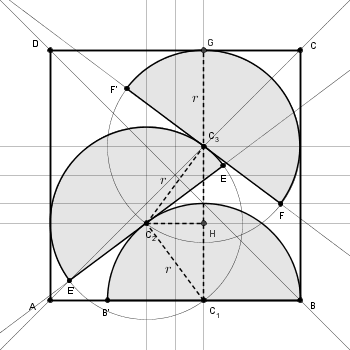
- panurgo_SC&Q008b.png (19.98 KiB) Visto 6579 volte
Se ora vogliamo mettere tre semicerchi tangenti con la base otteniamo questo massimo
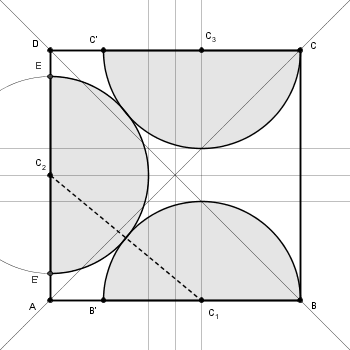
- panurgo_SC&Q015b.png (13.86 KiB) Visto 6579 volte
il cui raggio vale $r\,=\,\frac{\sqrt{19}\,-\,2}{6}$ essendo determinato dall’equazione
$\displaystyle \sqrt{4r^2\,-\,\frac14}\,+\,r\,=\,1$
Infine, nella mia soluzione, i due semicerchi tangenti con la base hanno la dimensione massima e il terzo semicerchio è ad essi tangente
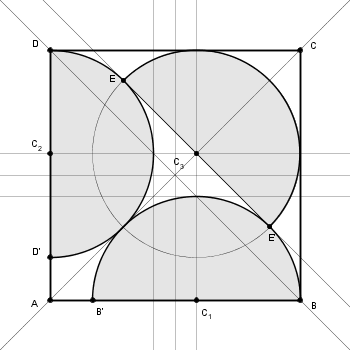
- panurgo_SC&Q010b.png (14.68 KiB) Visto 6579 volte
Spero che questo sia più convincente…