Figure e cuori

[delfo52]

appunto: il numero di carte in partenza e di carte rimanenti modifica i conti e si modifica in corso d'opera (a meno di giocare con infiniti mazzi.
Dovrebbe essere possibile determinare il numero di carte, e la lunghezza del gioco (magari fermandosi dopo n estrazioni, senza per forza esaurire le catrte), in modo da avere un perfetto 50% per ambo i giocatori

[Quelo]

Ho fatto altre simulazioni (sempre su un milione di partite), con mazzi diversi:
Mazzo minimo 19 carte (10 cuori / 9 figure): Pietro 58.7/59.9% - Paolo 40.1/41.3%
Mazzo ridotto 22 carte (13 cuori / 12 figure): Pietro 59.4/59.6% - Paolo 40.4/40.6%
Mazzo completo 52 carte (13 cuori / 12 figure): Pietro 60.4/60.8% - Paolo 39.2/39.6%
2 Mazzi completi 104 carte (26 cuori / 24 figure): Pietro 69.6/69.8% - Paolo 30.2/30.4%

Per controprova ho fatto anche una simulazione con 19 carte e 10 milioni di partite e il risultato è: Pietro 59.35% - Paolo 40.65%

--- AGGIORNAMENTO ---

Ho modificato la simulazione per aumentare la casualità nella disposizione delle carte, ora i risultati sono aderenti ai calcoli di Franco:

0,21822
-------------------
0,11346
-------------------
0,06885
-------------------
0,05217----0,00058
-------------0,00353
0,03541----0,01345
-------------0,03284
0,02882----0,06231
-------------0,09187
0,02364----0,10497
-------------0,08957
0,01534----0,04497

0,55592----0,44408

[Pasquale]

Mi sono perduto fra permutazioni, disposizioni e combinazioni...basta, mi arrendo.

[franco]

Ho sbirciato la soluzione del problema sul sito francese (http://www.diophante.fr) ma francamente non ci ho capito granché, se non che il numero finale somiglia molto al mio risultato.
Spero che il Panurgo mi illumini un po' di più (anche se purtroppo devo ammettere che a volte mi perdo nella sua simbologia ).

ciao

[Pasquale]

Nel frattempo, contrariamente alla precedente resa, vorrei provare ad affrontare una nuova strategia di calcolo che mi balenava per la testa poco fa.
Stavo pensando di calcolare la probabilità a favore di Pietro (quella di Paolo si deduce per differenza), considerando che i casi favorevoli a Pietro si sviluppano fra la seconda e la sedicesima carta scoperta (riferendosi alla situazione ridotta a 19 carte, che semplifica il problema), perché se alla sedicesima carta tutte le nove figure non sono state scoperte, Pietro non può più vincere.

Quindi, calcolo dei casi possibili con 1 carta scoperta e relativi casi favorevoli, casi possibili con 2 carte scoperte e relativi casi favorevoli, .......casi possibili con 16 carte scoperte e relativi casi favorevoli, nel senso di favorevoli a Pietro.

1 carta: casi possibili 19; favorevoli 0; prob. 0
2 carte: casi possibili D(19,2)=342; favorevoli D(9,2)=72; prob. 72/342=0,2105..
3 carte: casi poss. D(19,3)=5814; favorevoli D(9,3)=504; prob. 504/5814=0,0866..

non so se la strada è giusta e intanto mi fermo qui.

[panurgo]

Furegando nel sito francese di franco ho trovato questo problemino

Pietro propone a Paolo il seguente gioco: entrambi i giocatori debbono pagare una posta uguale; da un normale mazzo di carte francesi (ben mescolato) viene scoperta una carta alla volta; Pietro segna un punto ogni volta che esce una figura mentre Paolo lo fa ogni volta che esce una carta di cuori; Pietro vince se, in qualsiasi momento, si trova ad avere due punti più di Paolo e se ciò non accade, vince Paolo.
Fa bene Paolo ad accettare di giocare questo gioco?

Per prima cosa notiamo che ci sono alcune carte che sono di cuori ( ${\text C}$) mentre le altre non lo sono ( $\overline{\text C}$) e che alcune carte sono figure ( ${\text F}$) mentre le altre non lo sono ( $\overline{\text F}$): costruiamo una tabella di contingenza nella quale le carte sono così distribuite

$\begin{array}{c30|c30c30|c30C+30} & {\text C} & \overline{\text C} & \\ \hline {\text F} & 3 & 9 & 12 \\ \overline{\text F} & 10 & 30 & 40 \\ \hline & 13 & 19 & 52 \end{array}$

Se contiamo dal punto di vista di Pietro, ogni punto di Paolo è un punto negativo quindi sommiamo $+\/1$ per ogni figura che viene scoperta e $-\/1$ per ogni cuore: le trenta carte che non sono ne figure ne cuori assommano a zero e possono essere perciò del tutto omesse. Anche le tre figure di cuori valgono zero ( $+\/1$ in quanto figura e $-\/1$ in quanto cuore): le lasciamo perdere anch’esse.
Il mazzo così ridotto contiene perciò $9$ figure e $10$ cuori.

Per seconda cosa notiamo che quando Pietro vince è stato girato un numero pari di carte: $k\/-\/1$ carte di cuori e $k\/+\/1$ figure. Possiamo dunque girare le carte due a due.

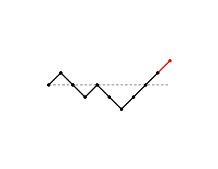
Possiamo rappresentare le carte uscite nelle varie mani con un grafo associando ad ogni figura (${\text F}$) un tratto obliquo ascendente e ad ogni cuore (${\text C}$) un tratto obliquo discendente: in tal modo la sequenza di carte ${\text FCCFCCFFFF}$ è rappresentata dal grafo



Ad ogni mano di due carte le uscite possibili sono ${\text FF}$, ${\text FC}$, ${\text CF}$ e ${\text CC}$ a cui corrispondono i grafi



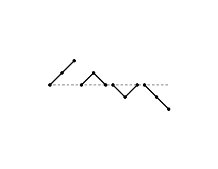
Sapendo che abbiamo $m$ cuori e $n$ figure assegnamo una probabilità a ciascuna mano

$\begin{array}{C+60} p\left({\text FF}\/\middle|\/m\/n\/I\right)\/=\/\frac{n\left(n-1\right)}{\left(m+n\right)\left(m+n-1\right)} \\ p\left({\text FC}\/\middle|\/m\/n\/I\right)\/=\/\frac{n\/m}{\left(m+n\right)\left(m+n-1\right)} \\ p\left({\text CF}\/\middle|\/m\/n\/I\right)\/=\/\frac{m\/n}{\left(m+n\right)\left(m+n-1\right)} \\ p\left({\text CC}\/\middle|\/m\/n\/I\right)\/=\/\frac{m\left(m-1\right)}{\left(m+n\right)\left(m+n-1\right)} \end{array}$

Osserviamo che la probabilità assegnata all’ipotesi che escano due carte di tipo diverso non dipende dall’ordine di uscita ( $n\/m\/=\/m\/n$). Ciò è vero in generale: ad ogni parola formata da un certo numero di ${\text F}$ e da un certo numero di ${\text C}$ assegneremo una probabilità che dipende da tali numeri ma non dall’ordine in cui le carte debbono uscire.
Infatti, se al primo passo è uscito ${\text FF}$, noi avremo $n\/-\/2$ figure e $m$ cuori, da cui

$p\left({\text FC}\/\middle|\/m\/n\/{\text FF}\/I\right)\/=\/p\left({\text CF}\/\middle|\/m\/n\/{\text FF}\/I\right)\/=\/\frac{\left(n-2\right)m}{\left(m+n-2\right)\left(m+n-3\right)}$

e

$p\left({\text FFFC}\/\middle|\/m\/n\/I\right)\/=\/p\left({\text FFCF}\/\middle|\/m\/n\/I\right)\/=\/\frac{n\left(n-1\right)\left(n-2\right)m}{\left(m+n\right)\left(m+n-1\right)\left(m+n-2\right)\left(m+n-3\right)}$

mentre se è uscito ${\text FC}$ (${\text CF}$) noi avremo $n\/-\/1$ figure e $m\/-\/1$ cuori, da cui

$p\left({\text FF}\/\middle|\/m\/n\/{\text FC}\/I\right)\/=\/p\left({\text FF}\/\middle|\/m\/n\/{\text CF}\/I\right)\/=\/\frac{\left(n-1\right)\left(n-2\right)}{\left(m+n-2\right)\left(m+n-3\right)}$

e

$p\left({\text FCFF}\/\middle|\/m\/n\/I\right)\/=\/p\left({\text CFFF}\/\middle|\/m\/n\/I\right)\/=\/\frac{n\left(n-1\right)\left(n-2\right)m}{\left(m+n\right)\left(m+n-1\right)\left(m+n-2\right)\left(m+n-3\right)}$

Q.E.D.

Le partite che terminano con la vittoria di Pietro sono rappresentate dai grafi della figura successiva



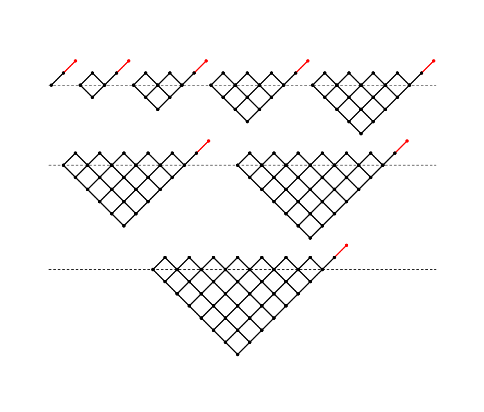
Ognuna di queste partite, il cui grafo termina raggiungendo quota $+\/2$ sulla linea di base, è costituita di $k$ mani con un totale di $k\/+\/1$ figure e $k\/-\/1$ cuori. Ogni grafo in figura rappresenta tutti i possibili modi in cui una partita di $k$ mani può terminare sul $+\/2$, ciascuno dei quali ha probabilità

$p\left({\text F}\/\cdots\/{\text C}\/\cdots\/\middle|\/m\/n\/I\right)\/=\/\frac{\overbrace{n\left(n-1\right)\cdots\left(n-k\right)}^{\script k+1}\/\times\/\overbrace{m\left(m-1\right)\cdots\left(m-k+2\right)}^{\script k-1}}{\underbrace{\left(m+n\right)\left(m+n-1\right)\cdots\left(m+n-2k+1\right)}_{\script 2k}}$

Per ottenerne una rappresentazione più compatta facciamo uso dei fattoriali

$p\left({\text F}\/\cdots\/{\text C}\/\cdots\/\middle|\/m\/n\/I\right)\/=\/\frac{\frac{n!}{\left(n-k-1\right)!}\/\times\/\frac{m!}{\left(m-k+1\right)!}}{\frac{\left(m+n\right)!}{\left(m+n-2k\right)!}}$

ovvero

$p\left({\text F}\/\cdots\/{\text C}\/\cdots\/\middle|\/m\/n\/I\right)\/=\/\frac{\frac{\left(m+n-2k\right)!}{\left(n-k-1\right)!\left(m-k+1\right)!}}{\frac{\left(m+n\right)!}{n!m!}}\/=\/\frac{m+n-2k\choose n-k-1}{m+n\choose n}$

Il coefficiente binomiale al denominatore conta in quanti modi il totale delle $m\/+\/n$ carte puo essere suddiviso nei due mucchi iniziali ($m$ e $n$ carte); quello al numeratore conta i modi in cui le carte residue possono essere suddivise nei due mucchi residui.

Dai grafi della figura precedente è possibile contare quante sono le partite per ogni valore di $k$ ma, se vogliamo una risposta generale, basta osservare che i grafi in questione hanno lo stesso numero di percorsi dei grafi della prossima figura



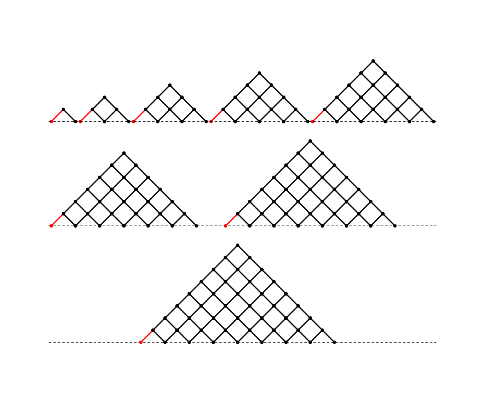
Questi grafi sono noti come cammini di Dyck (Dyck paths) e sono il soggetto di una vasta letteratura: si dimostra che i cammini di Dyck sono contati dai numeri di Catalan (1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796 ecc.) dati in formula chiusa da

$C_{\script k}\/=\/\frac1{k+1}{2k\choose k}$

Dunque, al probabilità che Pietro ha di vincere in $k$ mani e

$p\left(V\/k\/\middle|\/m\/n\/I\right)\/=\/\frac1{k+1}{2k\choose k}\frac{m+n-2k\choose n-k-1}{m+n\choose n}$

Sappiamo che Pietro vince in una mossa se esce ${\text FF}$ per cui deve essere $k\/\geq\/1$; inoltre, Pietro può vincere solo se $k\/\leq\/n\/-\/1$ perché il numero di figure residuo, $n\/-\/k\/-\/1$, non può essere minore di zero; per finire, se $n\/\geq\/m\/+\/2$ Pietro vince di sicuro: quindi, deve dunque essere $1\/\leq\/k\/<\/n\/\leq\/m\/+\/1$.
La probabilità di vittoria complessiva di Pietro si ottiene sommando le probabilità di vincere in $k$ mani per tutti i possibili valori di $k$

$p\left(V\/\middle|\/m\/n\/I\right)\/=\/\sum_{\script k}{p\left(V\/k\/\middle|\/m\/n\/I\right)}\/=\/\frac{\sum_{\script k=1}^{\script n-1}{\frac1{k+1}{2k\choose k}{m+n-2k\choose n-k-1}}}{m+n\choose n}\/=\/\frac{m+n\choose n-2}{m+n\choose n}\/=\/\frac{n\left(n-1\right)}{\left(m+2\right)\/\left(m+1\right)}$

Nel caso particolare, la probabilità è pari a $6/11$.


P.S.: l’identità

$\sum_{\script k=1}^{\script n-1}{\frac1{k+1}{2k\choose k}{m+n-2k\choose n-k-1}}\/=\/{m+n\choose n-2}$

è solo una congettura ma sto cercando una dimostrazione...

[Quelo]

Ho scovato un'imprecisione nell'albero di Franco, al quarto passaggio nel riquadro al centro c'è 1 1, invece dovrebbe esserci 1 2, se la si corregge i suoi risultati sono uguali a quelli di Panurgo.

[franco]

Ho scovato un'imprecisione nell'albero di Franco, al quarto passaggio nel riquadro al centro c'è 1 1, invece dovrebbe esserci 1 2, se la si corregge i suoi risultati sono uguali a quelli di Panurgo.

Grazie Sergio,

Mi ero riproposto di controllare bene l'albero questa sera a casa ma hai già individuato tu l'errore e quindi sono in pace.

Vedendo il lavoro di Guido mi sento più che soddisfatto di aver trovato la soluzione corretta numericamente; l'approccio teorico/analitico era fuori dalla mia portata:
cammini di Dyck, numeri di Catalan, tabelle di contingenza, ... tutto arabo per me

ciao

[Gianfranco]

Ragazzi, complimenti!
Ho seguito attentamente la discussione senza intervenire e ora mi inchino profondamente, in particolare a Franco per la sua soluzione che mi aveva convinto subito (a parte il piccolo errore) e a Panurgo per la soluzione dettagliata e i riferimenti ai cammini di Dyck e ai numeri di Catalan.

[panurgo]

Ho sbirciato la soluzione del problema sul sito francese [...]

Diamo un’occhiata alla figura seguente




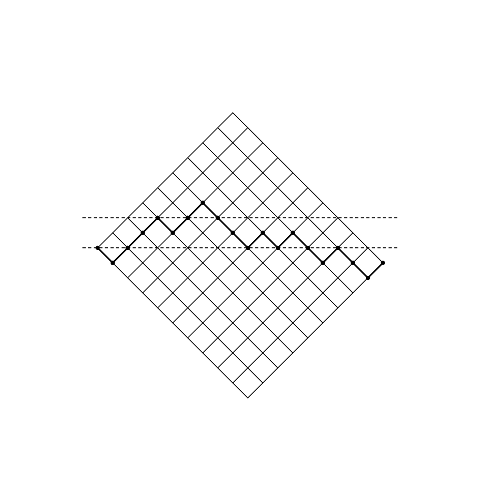
Un qualsiasi cammino sulla griglia rettangolare $10\/\times\/9$ rappresenta una permutazione del mazzo contenente $9$ figure e $10$ cuori.
Le due linee tratteggiate sono il livello $0$ e il livello $+\/2$.
Il cammino segnato è un esempio che rappresenta la permutazione ${\text CFFFCFFCCCFCFCCFCCF}$ che raggiunge il livello $+\/2$ alla quarta carta e corrisponde perciò ad una partita che termina con la vittoria di Pietro.

Se ora riflettiamo sulla linea del $+\/2$ la parte del cammino che precede il contatto con la linea stessa identifichiamo una nuova griglia




questa volta $12\/\times\/7$.
In questo modo abbiamo trovato una corrispondenza uno a uno (una biiezione) tra i cammini della prima griglia che raggiungono il livello $+\/2$, implicando con ciò la vittoria di Pietro, e quelli della seconda (se ci giocate un po’ ve ne convincerete).

Le permutazioni totali del mazzo (i cammini sulla griglia $m\/\times\/n$, nera) sono

${m+n\choose n}$

mentre le permutazioni che implicano la vittoria di Pietro (i cammini sulla griglia $m\/+\/2\/\times\/n\/-\/2$, rossa) sono

${m+n\choose n-2}$

e la probabilità di vittoria di Pietro è

$p\left(V\/\middle|\/m\/n\/I\right)\/=\/\frac{m+n\choose n-2}{m+n\choose n}\/=\/\frac{n\left(n-1\right)}{\left(m+2\right)\/\left(m+1\right)}$

Quindi, $6/11$.

Fra parentesi, questa è anche una dimostrazione dell’identità

$\sum_{\script k=1}^{\script n-1}{\frac1{k+1}{2k\choose k}{m+n-2k\choose n-k-1}}\/=\/{m+n\choose n-2}$

da me congetturata nel post precendente