Penney ante

[panurgo]

Qui

c) Penney ante (proposto e risolto da Walter Penney, JRM 2:4 (Ottobre1969), discusso da Donald Knuth nel libro Concrete Mathematics del 1994)
Si usa una moneta non truccata. Il primo giocatore sceglie una sequenza di tre uscite, es. TTC. Il secondo giocatore, dopo aver saputo la sequenza scelta dal primo, sceglie a sua volta un'altra tripla, es. CTT. Si lancia la moneta fino a quando esce una delle due triple. Vince chi ha scelto la tripla che esce per prima.

Una domanda.
Gioco del Penney ante:
Qual è la probabilità che TCC esca prima di CCT?

Così, a naso, direi $3/4$...

[panurgo]

Nessuno è curioso...


...o Qualcuno è curioso

[Pasquale]

Pan, non è che non siamo curiosi, ma a volte capita che non ci sia tempo da dedicare al forum, oppure che non si quagli una risposta.
Nel mio caso non ho quagliato nemmeno la domanda, perché prima ne avrei una da fare.
Se una combinazione ha più probabilità di un'altra di sortire per prima, significa anche che in genere ha più probabilità dell'altra di essere sortita?
Voglio dire, ad esempio: su una sequenza di 1000 tiri, si possono individuare più combinazioni TCC che CCT ? In caso positivo, sarebbe anche più probabile la sortita per prima, essendovene di più.
Comunque non ho avuto tempo nemmeno di effettuare una delle solite opinabili simulazioni.
Direi comunque di lasciare più tempo (una volta si diceva che anche un anno sarebbe congruo).

[panurgo]

[...] a volte capita che non ci sia tempo da dedicare al forum, oppure che non si quagli una risposta [...]

Non me ne parlare! Comunque la mia risposta non è ancora pronta: volevo davvero sapere se la cosa vi incuriosisce.

[Pasquale]

si, la risposta è si

[Pasquale]

Dunque ho effettuato delle simulazioni che confermano il tuo risultato.
E' incredibile e non riesco a capire il perché.
L'unica spiegazione che mi sento di azzardare è che TCC presenta prima una variazione e poi una ripetizione, mentre CCT presenta prima una ripetizione e poi una variazione.
Se eseguo una simulazione con CTT e TTC, che presentano le stesse caratteristiche, il risultato resta sui 3/4 a favore di CTT, che presenta prima la variazione.

Interessanti altri confronti:

TTT e CCC : 1/2

TCT e CTC : 1/2

Fra TCT e TTC (2 variazioni contro 1 permanenza e 1 variazione) la prima combinazione si aggiudica stranamente solo 1/3, mentre fra TCT e TCC (2 variazioni contro 1 variazione e 1 permanenza) siamo al 50%.

Fra TCC e CCC, 87% a favore della prima combinazione.

Direi che la cosa si fa sempre più interessante ed alla luce di tali risultati, in relazione al gioco proposto, direi che il secondo giocatore, dovendo scegliere la sua combinazione, essendo nota la scelta del primo, è sempre in grado di vincere o almeno pareggiare.

[Massimo]

mi pare anche a me che sia 1/2 * 1/2 = 1/4

[Admin]

Ciao a tutti,
a me è sembrata semplice la questione.

Questo il ragionamento:
- se al primo lancio si ha $T$, allora sicuramente la sequenza $TCC$ sarà la prima ad uscire
- se al primo lancio si ha $C$, ed al secondo si ha $T$, anche in questo caso la sequenza $TCC$ sarà la prima ad uscire
- se invece al primo lancio si ha $C$, ed al secondo si ha ancora $C$, allora in questo caso sarà la sequenza $CCT$ ad uscire per prima

Pertanto indicando con:

$p(T\/|\/I)$ : probabilità che al primo lancio si abbia $T$
$p(TC\/|\/I)$ : probabilità che al primo lancio si abbia $C$, ed al secondo $T$
$p(S\/|\/I)$: probabilità che $TCC$ esca prima di $CCT$

si ha, semplicemente che:

$p(S\/|\/I)\/=\/p(T\/|\/I)\/+\/p(TC\/|\/I)\/=\/\frac{1}{2}\/+\/\frac{1}{2}\/\cdot\/\frac{1}{2}\/=\/\frac{3}{4}$

Ma conoscendo il buon Panurgo, probabilmente ho dimenticato qualcosa ...

Saluti
Admin

[Pasquale]

Questo il ragionamento:
- se al primo lancio si ha T , allora sicuramente la sequenza TCC sarà la prima ad uscire
- se al primo lancio si ha C, ed al secondo si ha T, anche in questo caso la sequenza TCC sarà la prima ad uscire
- se invece al primo lancio si ha C, ed al secondo si ha ancora C, allora in questo caso sarà la sequenza CCT ad uscire per prima

....è vero, non ci avevo pensato, è giusto, elementare Watson! (ho avuto dei miraggi)

[panurgo]

Le sequenze di teste ($\mathbb{T}$) e croci ($\mathbb{C}$) corrispondono ad altrettante parole ottenute dall’alfabeto di due lettere $\left\{\mathbb{T}, \mathbb{C}\right\}$: se indichiamo con $\epsilon$ la parola vuota (la parola di zero lettere) l’insieme delle parole possibili è

$\left\{ \epsilon, \/\mathbb{T}, \/\mathbb{C}, \/\mathbb{TT}, \/\mathbb{TC}, \/\mathbb{CT}, \/\mathbb{CC}, \/\mathbb{TTT}, \/\mathbb{TTC}, \/\mathbb{TCT}, \/\mathbb{TCC}, \/\mathbb{CTT}, \/\mathbb{CTC}, \/\mathbb{CCT}, \/\mathbb{CCC}, \/\cdots\/\right\}$

Vi è una parola di zero lettere, due di una lettera, quattro di due ecc.: in generale le parole di $n$ lettere sono $2^{\script n}$. Per assegnare ai due giocatori le probabilità di vittoria, condizionate alle triplette scelte, è sufficiente contare le parole di lunghezza infinita in cui una delle triplette compare prima dell’altra e quelle in cui è vero il contrario.
Dal punto di vista del processo, una volta che è apparsa una delle triplette il gioco termina: quella parola conta anche per tutte le parole che possono essere formate allungando la parola stessa. Per capirci, la tripletta $\mathbb{TTT}$ è una su otto triplette e questo significa che $1/8$ delle parole di lunghezza infinita inizia così; il quadrupletto $\mathbb{CTTT}$, che termina anch’esso (ma non comincia) su $\mathbb{TTT}$, è uno su sedici quindi conta per $1/16$ delle parole possibili ecc.
Descriviamo i primi tre passi del processo con un grafo (tre passi sono necessari per ottenere una tripletta)



Dopo la prima lettera le frecce verdi rappresentano transizioni che ripetono l’ultima lettera, quelle rosse transizioni che cambiano lettera: osserviamo che, disegnato in questo modo, il grafo ha un asse di rotazione binario, $S_{\script 2}$, che corrisponde allo scambio di $\mathbb{T}$ con $\mathbb{C}$.
Oltre che per rendere evidente questa simmetria vi è un altro motivo per questo arrangiamento: puliamo innanzitutto il grafo cancellando i primi passi



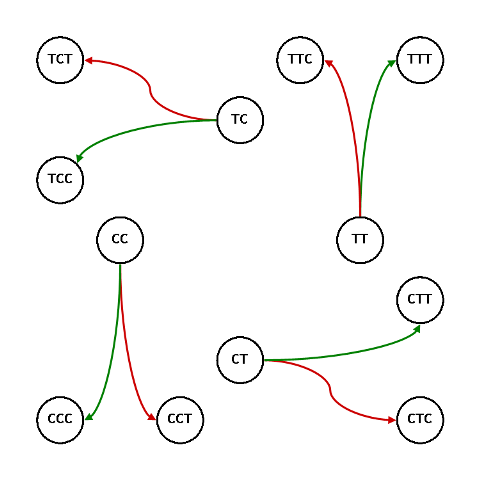
Se adesso consideriamo solo le ultime due lettere di ogni parola, nel processo abbiamo quattro stati possibili, collegati in questo modo



Ciascuna transizione porta ad una parola, più lunga di una lettera, la cui terminazione è ancora uno dei quattro doppietti.
Ora non resta che scegliere le triplette di chiusura e collegarle con le relative transizioni per ottenere il grafo di tutti i processi possibili in questo gioco: se, per esempio, scegliamo le triplette $\mathbb{TTT}$ e $\mathbb{TTC}$ il grafo corrispondente è



Il grafo di base conserva la simmetria $S_{\script 2}$ del grafo originale cosicché il primo giocatore ha solo quattro possibilità di scelta non equivalenti tra loro



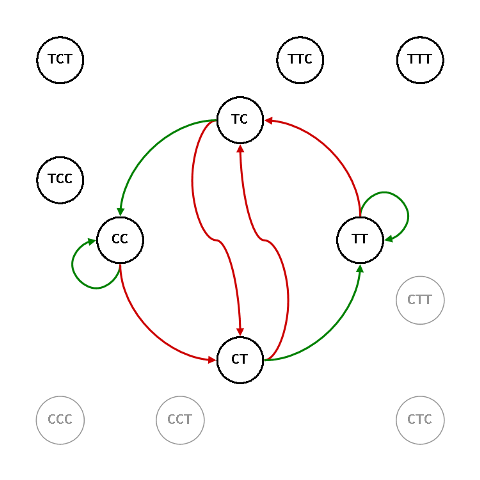
Le quattro triplette che iniziano per $\mathbb{C}$ (in basso nel grafo) sono equivalenti, sotto $S_{\script 2}$, alle quattro che iniziano per $\mathbb{T}$ (in alto nel grafo).
Il grafo perde la sua simmetria una volta tolta una tripletta e il secondo giocatore ha a disposizione sette triplette, nessuna delle quali equivale a nessun’altra.
Numeriamo ora gli stati nel verso trigonometrico a partire da $\mathbb{TTT}$ ($1$), $\mathbb{TTC}$ ($2$), $\mathbb{TCT}$ ($3$) ecc.: ai fini dell’analisi è sufficiente considerare per il secondo giocatore le triplette successive a quella scelta dal primo. Il grafo G12 ($\mathbb{TTT}$ contro $\mathbb{TTC}$) non è diverso da G21 ($\mathbb{TTC}$ contro $\mathbb{TTT}$).

Confronteremo le probabilità di vittoria dei due giocatori, al modo anglosassone, mediante gli “odds”: il rapporto tra le probabilità. Se la probabilità di ciascun giocatore è $1/2$ allora gli odds sono $1:1$; se le probabilità sono $1/3$ e $2/3$ allora gli odds sono $1:2$ ecc.
Raccoglieremo gli odds in una tabella, le cui righe corrispondono alla scelta del primo giocatore e le colonne a quella del secondo,

$\begin{array}{c50|c50c50c50c50c50c50c50c50|C+50} & {\script \mathbb{TTT}} & {\script\mathbb{TTC}} & {\script\mathbb{TCT}} & {\script\mathbb{TCC}} & {\script\mathbb{CCC}} & {\script\mathbb{CCT}} & {\script\mathbb{CTC}} & {\script\mathbb{CTT}} \\ \hline {\script\mathbb{TTT}} & \times & \mathcal{O}_{\script 12} &\mathcal{O}_{\script 13} & \mathcal{O}_{\script 14} & \mathcal{O}_{\script 15} & \mathcal{O}_{\script 16} & \mathcal{O}_{\script 17} & \mathcal{O}_{\script 18} \\ {\script \mathbb{TTC}} & O_{\script 12}^{\script -1} & \times & \mathcal{O}_{\script 23} & \mathcal{O}_{\script 24} & \mathcal{O}_{\script 25} & \mathcal{O}_{\script 26} & \mathcal{O}_{\script 27} & \mathcal{O}_{\script 28} \\ {\script \mathbb{TCT}} & O_{\script 13}^{\script -1} & O_{\script 23}^{\script -1} &\times & \mathcal{O}_{\script 34} &\mathcal{O}_{\script 35} & \mathcal{O}_{\script 36} & \mathcal{O}_{\script 37} & \mathcal{O}_{\script 38} \\ {\script\mathbb{TCC}} & O_{\script 14}^{\script -1} & O_{\script 24}^{\script -1} & O_{\script 34}^{\script -1} & \times & \mathcal{O}_{\script 45} & \mathcal{O}_{\script 46} & \mathcal{O}_{\script 47} & \mathcal{O}_{\script 48} \\ {\script\mathbb{CCC}} & O_{\script 15}^{\script -1} & O_{\script 25}^{\script -1} & O_{\script 35}^{\script -1} & O_{\script 45}^{\script -1} & \times & O_{\script 12} & O_{\script 13} & O_{\script 14} \\ {\script\mathbb{CCT}} & O_{\script 16}^{\script -1} & O_{\script 26}^{\script -1} & O_{\script 36}^{\script -1} & O_{\script 46}^{\script -1} & O_{\script 12}^{\script -1} & \times & O_{\script 23} & O_{\script 24} \\ {\script\mathbb{CTC}} & O_{\script 17}^{\script -1} & O_{\script 27}^{\script -1} & O_{\script 37}^{\script -1} & O_{\script 47}^{\script -1} & O_{\script 13}^{\script -1} & O_{\script 23}^{\script -1} & \times & O_{\script 34} \\ {\script\mathbb{CTT}} & O_{\script 18}^{\script -1} & O_{\script 28}^{\script -1} & O_{\script 38}^{\script -1} & O_{\script 48}^{\script -1} & O_{\script 14}^{\script -1} & O_{\script 24}^{\script -1} & O_{\script 34}^{\script -1} & \times \\ \hline\end{array}$

nelle caselle del triangolo inferiore gli odds sono inversi a quelli delle caselle simmetriche rispetto alla diagonale principale; nelle ultime sei caselle del triangolo superiore, in basso a destra, gli odds sono gli stessi delle prime sei caselle in alto a sinistra per via della simmetria $S_{\script 2}$.

Alcuni dei nostri grafi sono di semplicissima interpretazione: per esempio, il grafo G12 ($\mathbb{TTT}$ contro $\mathbb{TTC}$) visto in precedenza



evidenzia che tutte le parole che terminano sulle triplette prescelte lo fanno dopo aver raggiunto lo stato $\mathbb{TT}$: tutto quello che precede è identico e l’unica differenza è nell’ultima lettera. Non ci interessa sapere quante siano in totale queste parole ma solo che le due triplette hanno frequenza uguale.
Per questo tipo di grafico “bifido” gli odds sono $\mathcal{O}_{\script 12}\/=\/1:1$. Ce ne sono altri tre: G34 ($\mathbb{TCT}$ contro $\mathbb{TCC}$), G56 ($\mathbb{CCC}$ contro $\mathbb{CCT}$) e G78 ($\mathbb{CTC}$ contro $\mathbb{CTT}$). Sotto $S_{\script 2}$ G56 è equivalente a G12 e G78 è equivalente a G34.



Un altro esempio di grafo facilmente interpretabile è G15 ($\mathbb{TTT}$ contro $\mathbb{CCC}$)



Le due triplette prescelte sono equivalenti per simmetria: qualunque percorso seguiamo per arrivare in $\mathbb{TTT}$, per quanto complicato, è associato biunivocamente con il percorso che si ottiene scambiando $\mathbb{T}$ con $\mathbb{C}$, e che porta in $\mathbb{CCC}$: gli odds sono di nuovo $\mathcal{O}_{\script 15}\/=\/1:1$. Di questi grafi “simmetrici” ce ne sono altri tre: G26 ($\mathbb{TTC}$ contro $\mathbb{CCT}$), G37 ($\mathbb{TCT}$ contro $\mathbb{CTC}$) e G48 ($\mathbb{TCC}$ contro $\mathbb{CTT}$).



Ecco ancora G27, $\mathbb{TTC}$ contro $\mathbb{CTC}$



Questo grafico è pseudobifido: tutto quello che viene prima di $\mathbb{CT}$ è comune alle due parole; metà va a $\mathbb{CT}$ (con frequenza complessiva $3/8$) e l’altra metà si aggiunge alle parole che iniziano con $\mathbb{TT}$ (con frequenza complessiva $5/8$).

Gli odds sono: $\mathcal{O}_{\script 27}\/=\/5:3$.

Il suo simmetrico è G36, $\mathbb{TCT}$ contro $\mathbb{CCT}$



e gli odds sono: $\mathcal{O}_{\script 36}\/=\/3:5$.

Continuiamo con G28 ($\mathbb{TTC}$ contro $\mathbb{CTT}$):



In questo caso il grafo è diviso in due sottografi disgiunti: evidentemente la frequenza con cui il processo termina in $\mathbb{TTC}$ è $1/4$ e quella con cui termina in $\mathbb{CTT}$ è $3/4$, ovvero la frequenza di ingresso nei due sottografi: gli odds sono $\mathcal{O}_{\script 15}\/=\/1:3$.

Il grafo G46, quello relativo al confronto $\mathbb{TCC}/\mathbb{CTT}$, è equivalente a questo, sotto $S_{\script 2}$.



Gli odds sono ovviamente $\mathcal{O}_{\script 15}\/=\/3:1$.

Non sono difficili da interpretare neanche i grafi G18 ($\mathbb{TTT}$ contro $\mathbb{CTT}$)



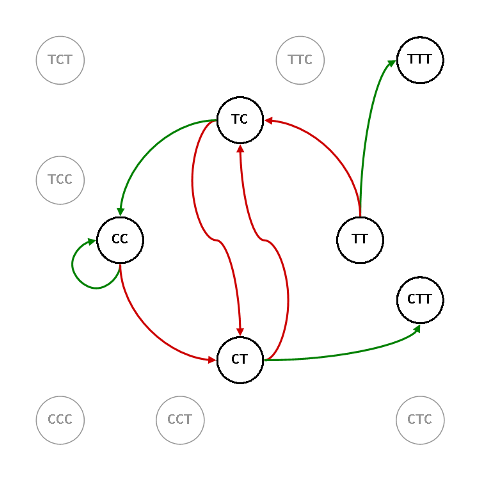
e il suo simmetrico, G45 ($\mathbb{TCC}$ contro $\mathbb{CCC}$)



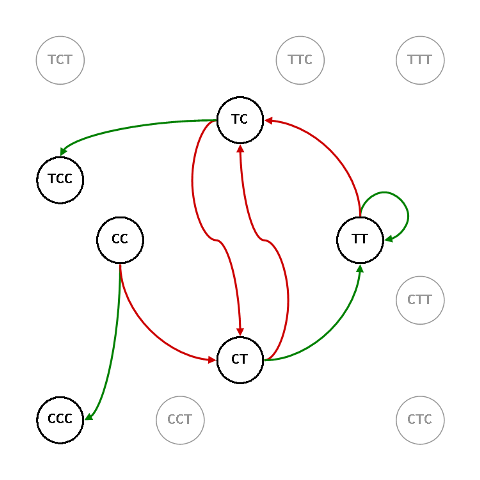
Gli stati $\mathbb{TTT}$ e $\mathbb{CCC}$ rispettivamente sono raggiungibili solo al terzo passo, entrando al secondo passo in $\mathbb{TT}$ ($\mathbb{CC}$): le frequenze di $\mathbb{TTT}$ e $\mathbb{CCC}$ sono pari a $1/8$, quelle di $\mathbb{CTT}$ e $\mathbb{TCC}$ a $7/8$. E gli odds sono $\mathcal{O}_{\script 18}\/=\/1:7$ e $\mathcal{O}_{\script 15}\/=\/7:1$. Il giocatore che, da primo di mano, sceglie $\mathbb{TTT}$ o $\mathbb{CCC}$ non potrebbe fare di peggio.

Fin qui, le interpretazioni facili. Quasi, direi, qualitative. Vediamo adesso come i nostri grafi possano aiutarci a quantificare anche i casi più complessi considerando il grafo di base del processo.



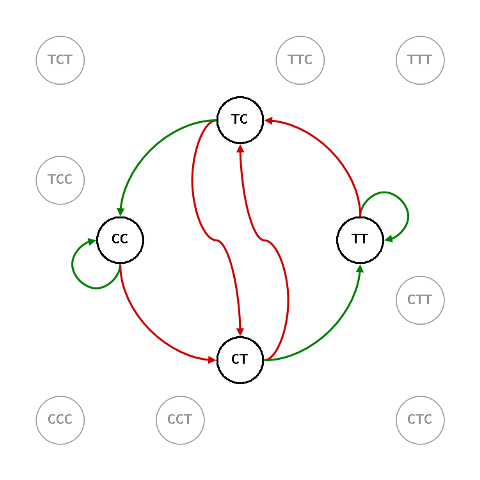
Supponiamo di avere una parola che termina con $\mathbb{CT}$. Lo stato $\mathbb{TC}$ viene raggiunto in un passo da metà delle parole: l’altra metà passa nello stato $\mathbb{TT}$ ma, in un numero indeterminato di passi finirà per arrivare anch’essa in $\mathbb{TC}$. Intuitivamente è ovvio che, a parte la singola parola $\cdots \/\mathbb{CTTT}\/\cdots$ (con infinite $\mathbb{T}$), se partiamo da $\mathbb{CT}$ alla fine dovremo arrivare a $\mathbb{TC}$.
Questo significa che le due transizioni

$\mathbb{CT}\/\rightarrow \/\mathbb{TC}$

e

$\mathbb{CT}\/\rightarrow \/\left(\mathbb{TT}\right)_{\script n}\/\rightarrow \/\mathbb{TC}$

devono essere equivalenti, ciascuna con frequenza $1/2$.

Per capire come, spostiamo la nostra attenzione sullo stato $\mathbb{TT}$. Questo stato ha una transizione in ingresso, una in uscita e un ciclo: schematicamente



Le tre transizioni hanno le frequenze $f_{\script i}$, $f_{\script u}$ e $f_{\script c}$ rispettivamente; il numero di volte che il ciclo viene percorso può essere qualunque e dobbiamo considerare tutte le possibilità: tenuto conto che due transizioni in serie sono equivalenti ad una transizione la cui frequenza è data dal prodotto delle due frequenze mentre due transizioni in parallelo sono equivalenti ad una transizione la cui frequenza è data dalla somma delle due frequenze (transizioni in parallelo si sommano, transizioni in serie si moltiplicano) abbiamo

$\begin{array}{c80|c80C+30} {\text num. cicli} & {\text frequenza} \\ \hline 0 & f_{\script i}\/f_{\script u} \\ 1 & f_{\script i}\/f_{\script c}\/f_{\script u} \\ 2 & f_{\script i}\/f_{\script c}^{\script 2}\/f_{\script u} \\ \vdots & \vdots \\ n & f_{\script i}\/f_{\script c}^{\script n}\/f_{\script u} \\ \vdots & \vdots \end{array}$

e quindi il ciclo è equivalente ad una transizione di frequenza

$f_{\script e}\/=\/f_{\script i}\/\left(1\/+\/f_{\script c}\/+\/f_{\script c}^{\script 2}\/+\/\cdots\/\right)\/f_{\script u}\/=\/\frac{f_{\script i}\/\times\/f_{\script u}}{1-f_{\script c}}$

perché all’interno delle parentesi abbiamo una serie geometrica di ragione $f_{\script c}$.
Nel caso particolare $f_{\script i}\/=\/f_{\script c}\/=\/f_{\script u}\/=\/\frac12$ quindi

$f_{\script e}\/=\/\frac{\frac12\times\frac12}{1-\frac12}\/=\/\frac12$

q.e.d.

La simmetria del grafo ci assicura che le medesime considerazioni valgono per le transizioni che partono dallo stato $\mathbb{TC}$.

Vediamo ora qual è il fato delle transizioni che partono da $\mathbb{TT}$. Visto da $\mathbb{TT}$, il grafo appare come un ciclo concatenato: infatti, abbiamo appena visto che da $\mathbb{TT}$ è giocoforza arrivare in $\mathbb{TC}$ e da $\mathbb{TC}$ in $\mathbb{CT}$; viceversa, la frequenza della transizione

$\mathbb{CT}\/\rightarrow \/\mathbb{TT}$

è solo $1/2$ e metà delle parole continua il ciclo

$\mathbb{CT}\/\rightarrow \/\mathbb{TC}\/\rightarrow \/\left(\mathbb{CC}\right)_{\script n}\/\rightarrow \/\mathbb{CT}$

Schematicamente



La frequenza equivalente del ciclo concatenato è

$f_{\script e}\/=\/\frac{1\times\frac12}{1-\frac12}\/=\/1$

quindi il processo ritornerà inevitabilemente in $\mathbb{TT}$.
A rischio di ripetermi, lo stato $\mathbb{TT}$ e lo stato $\mathbb{CC}$ sono simmetrici sotto $S_{\script 2}$ quindi le considerazioni fatte per il primo si applicano anche al secondo.

Armati di questi ragionamenti andiamo a scoprire come si comporta il processo descritto dal primo grafo finora non considerato: il grafo G13, corrispondente al confronto $\mathbb{TTT}$ contro $\mathbb{TCT}$.



Per prima cosa, il processo, dal punto di vista di $\mathbb{TC}$, può essere rappresentato come un ciclo semplice



La transizione $u$ è $\mathbb{TC}\/\rightarrow \/\mathbb{TCC}$, con $f_{\script u}\/=\/1/2$; la transizione $c$ è formata da due cicli in parallelo,

$\mathbb{TC}\/\rightarrow \/\left(\mathbb{CC}\right)_{\script n}\/\rightarrow \/\mathbb{CT}\/\rightarrow \/\mathbb{TC}$

e

$\mathbb{TC}\/\rightarrow \/\left(\mathbb{CC}\right)_{\script n}\/\rightarrow \/\mathbb{CT}\/\rightarrow \/\mathbb{TT}\/\rightarrow \/\mathbb{TC}$

Abbiamo visto prima che la frequenza equivalente della transizione $\mathbb{TC}\/\rightarrow \/\left(\mathbb{CC}\right)_{\script n}\/\rightarrow \/\mathbb{CT}$ è $1/2$ per cui la frequenza del primo ciclo è $1/4$ mentre quella del secondo è $1/8$ (ha una transizione in più): i cicli sono in parallelo per cui $f_{\script c}\/=\/3/8$.
Non ci resta ora che vedere quanto vale $f_{\script i}$.
Ricordiamoci che il grafo non mostra i primi due passi del processo e che quindi ogni stato ha una frequenza di ingresso al secondo passo di $1/4$. Possiamo dunque entrare in $\mathbb{TC}$ al secondo passo con frequenza $1/4$; entrare in $\mathbb{TT}$ e di lì entrare in $\mathbb{TC}$ al terzo passo (frequenza $1/8$); oppure entrare in $\mathbb{CT}$ e di lì passare a $\mathbb{TC}$ con una delle due transizioni in parallelo al terzo e al quarto passo (frequenza $3/16$); infine, se entriamo da $\mathbb{CC}$ passiamo a $\mathbb{CT}$ con certezza, anche se con un numero di passi incognito, e la frequenza di transizione a $\mathbb{TC}$ è ancora $3/16$.
Sommando queste possibilità otteniamo $f_{\script i}\/=\/3/4$.
La frequenza con cui il processo termina su $\mathbb{TCT}$ è quindi

$f_{\script e}\/=\/\frac{\frac34\times\frac12}{1-\frac38}\/=\/\frac35$

Ne consegue che la frequenza con cui il processo termina su $\mathbb{TTT}$ deve essere $2/5$: verifichiamolo.
Dal punto di vista di $\mathbb{TT}$ il processo un ciclo concatenato, con $f_{\script u}\/=\/1/2$



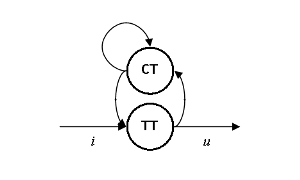
La frequenza della transizione

$\mathbb{TT}\/\rightarrow \/\mathbb{TC}\/\rightarrow \/\left(\mathbb{CC}\right)_{\script n}\/\rightarrow \/\mathbb{CT}$

è $1/4$ perchè valgono $1/2$ sia la frequenza della transizione

$\mathbb{TT}\/\rightarrow \/\mathbb{TC}$

sia quella equivalente di

$\mathbb{TC}\/\rightarrow \/\left(\mathbb{CC}\right)_{\script n}\/\rightarrow \/\mathbb{CT}$

La frequenza del ciclo concatenato

$\mathbb{CT}\/\rightarrow \/\mathbb{TC}\/\rightarrow \/\left(\mathbb{CC}\right)_{\script n}\/\rightarrow \/\mathbb{CT}$

vale anch’essa $1/4$ mentre la frequenza di uscita da tale ciclo è $1/2$.
La frequenza equivalente del ciclo è perciò

$f_{\script c}\/=\/\frac{\frac14\times\frac12}{1-\frac14}\/=\/\frac16$.

Valutiamo ora $f_{\script i}$.
L’ingresso diretto in $\mathbb{TT}$ al secondo passo ha frequenza $1/4$ mentre l’ingresso al secondo passo in uno qualunque degli altri tre stati comporta l’immissione nel ciclo concatenato

$\mathbb{CT}\/\rightarrow \/\mathbb{TC}\/\rightarrow \/\left(\mathbb{CC}\right)_{\script n}\/\rightarrow \/\mathbb{CT}$

Consideriamo dunque l’ingresso diretto in $\mathbb{CT}$ al secondo passo (frequenza $1/4$), l’ingresso da $\mathbb{CC}$ dopo un numero indefinito di passi (frequenza $1/4$) e l’ingresso da $\mathbb{TC}$ via $\mathbb{CC}$ dopo un numero indefinito di passi (frequenza $1/8$): l’uscita dal ciclo concatenato ha frequenza $1/2$ quindi

$f_{\script i}\/=\/\frac14\/+\/\frac{\frac58\times\frac12}{1-\frac14}\/=\/\frac23$.

La frequenza con cui il processo termina su $\mathbb{TTT}$ è perciò

$f_{\script i}\/=\/\frac{\frac23\times\frac12}{1-\frac16}\/=\/\frac25$.

q.e.d.

Gli odds sono $\mathcal{O}_{\script 13}\/=\/2:3$.

Procediamo ora speditamente con G14, $\mathbb{TTT}$ contro $\mathbb{TCC}$.



La transizione $\left(\mathbb{CC}\right)_{\script n}\/\longrightarrow \/\mathbb{CT}$ è certa (in un numero incognito di passi) ragion per cui il grafo è equivalente al precedente con la sostituzione di

$\mathbb{TC}\/\longrightarrow \/\left(\mathbb{CC}\right)_{\script n}\/\longrightarrow \/\mathbb{CT}$

con

$\mathbb{TC}\/\longrightarrow \/\mathbb{CT}$

Cambiano le modalità di ingresso ma non il risultato: $\mathcal{O}_{\script 14}\/=\/2:3$.

Sotto $S_{\script 2$, a G13 corrisponde G57



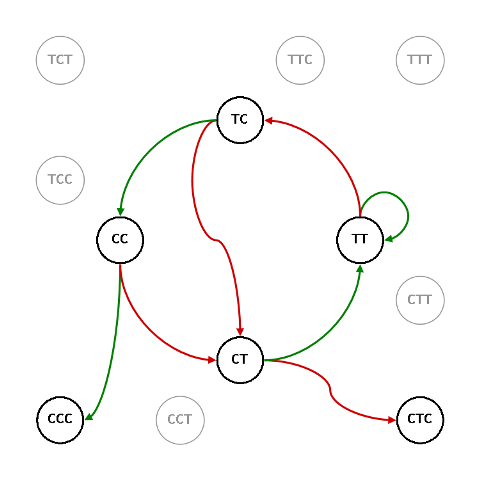
e a G14 corrisponde G58



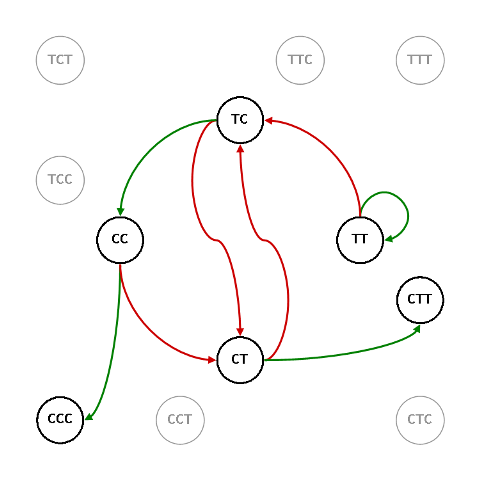
Quindi, $\mathcal{O}_{\script 57}\/=\mathcal{O}_{\script 58}\/=\/2:3$.

Vediamo ora qualcosa di diverso: G16, $\mathbb{TTT}$ contro $\mathbb{CCT}$.



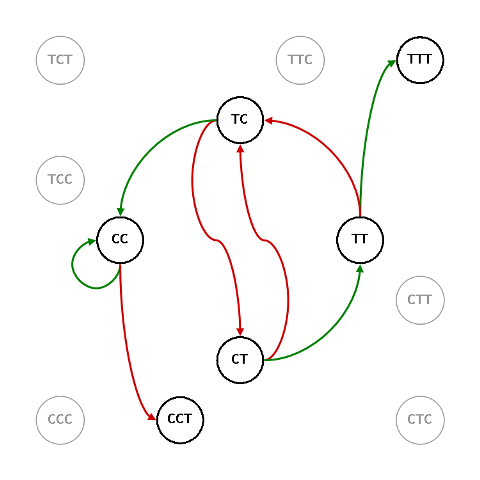
Il processo, visto da $\mathbb{TT}$ è un ciclo concatenato

$\mathbb{TT}\/\longrightarrow \/\left(\mathbb{TC}\longrightarrow \/\mathbb{CT}\longrightarrow \/\mathbb{TC}\right)_{\script n}\/\longrightarrow \/\mathbb{TT}$

La transizione di uscita $u$ è $\mathbb{TT}\/\longrightarrow \/\mathbb{TTT}$, con $f_{\script u}\/=\/1/2$.
La frequenza equivalente del ciclo concatenato è

$f_{\script c}\/=\/\frac{\frac14\times\frac12}{1-\frac14}\/=\/\frac16$

dove $1/4$ è la frequenza equivalente di $\mathbb{TT}\/\longrightarrow \mathbb{TC}\longrightarrow \/\mathbb{CT}$ (ingresso nel ciclo concatenato), $1/2$ è la frequenza di $\mathbb{CT}\/\longrightarrow \mathbb{TT}$ (uscita dal ciclo concatenato) e, al denominatore, $1/4$ è la frequenza equivalente del ciclo $\mathbb{CT}\/\longrightarrow \mathbb{TC}\longrightarrow \/\mathbb{CT}$.
La frequenza (equivalente) di ingresso è

$f_{\script i}\/=\/\frac14\/+\/\frac{\left(\frac14+\frac18\right)\times\frac12}{1-\frac14}\/=\/\frac12$

dove, in ordine, $1/4$ è l’ingresso diretto in $\mathbb{TT}$ al secondo passo; $1/4$ è l’ingresso diretto in $\mathbb{CT}$ al secondo passo; $1/8$ è l’ingresso in $\mathbb{CT}$ al terzo passo proveniendo da $\mathbb{TC}$; $1/2$ è la frequenza di uscita dal ciclo concatenato; al denominatore, $1/4$ è di nuovo la frequenza equivalente del ciclo

$\mathbb{CT}\/\longrightarrow \mathbb{TC}\longrightarrow \/\mathbb{CT}$

Quindi

$f_{\script e}\/=\/\frac{\frac12\times\frac12}{1-\frac16}\/=\/\frac3{10}$

è la frequenza con cui il processo termina su $\mathbb{TTT}$.
Vogliamo verificare che la frequenza di terminazione su $\mathbb{CCT}$ è $7/10$?
Il ciclo del processo esclude $\mathbb{CC}$ quindi lo guarderemo dal punto di vista di $\mathbb{TC}$: un ciclo semplice con $f_{\script u}\/=\/1/2$ ($\mathbb{TC}\/\longrightarrow \mathbb{CC}$), $f_{\script u}\/=\/3/8$ ($\mathbb{TC}\/\longrightarrow \mathbb{CT}\/\longrightarrow \mathbb{TC}$ e $\mathbb{TC}\/\longrightarrow \mathbb{CT}\/\longrightarrow \mathbb{TT}\/\longrightarrow \mathbb{TC}$) e

$f_{\script i}\/=\/\frac14\/+\/\frac18\/+\/\frac18\/+\/\frac1{16}\/=\/\frac9{16}$

(ingresso diretto + ingresso al terzo passo da $\mathbb{TT}$ + ingresso al terzo passo da $\mathbb{CT}$ + ingresso al quarto passo da $\mathbb{CT}\/\longrightarrow \mathbb{TT}$) equivalente ad una transizione di frequenza

$f_{\script e}\/=\/\frac{\frac9{16}\times\frac12}{1-\frac38}\/=\/\frac9{20}$

Per ottenere la frequenza cercata dobbiamo solo sommare la frequenza di ingresso al secondo passo in $\mathbb{CC}$

$f\/=\/\frac9{20}\/+\/\frac14\/=\/\frac7{10}$

q.e.d.

E gli odds sono: $\mathcal{O}_{\script 16}\/=\/3:7$.

Il suo simmetrico è G25, $\mathbb{TTC}$ contro $\mathbb{CCC}$



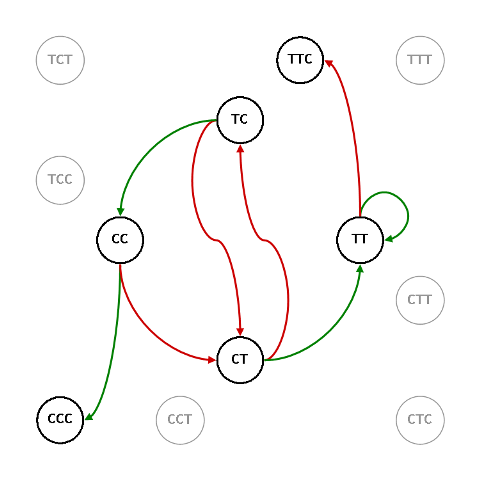
e i suoi odds sono: $\mathcal{O}_{\script 25}\/=\/7:3$.

G17, $\mathbb{TTT}$ contro $\mathbb{CTC}$



In questo caso, tutta la parte sinistra corrisponde al grafo di base: tutto ciò che parte da $\mathbb{TC}$ e da $\mathbb{CC}$ arriva inevitabilmente in $\mathbb{CT}$; metà di quello che parte da $\mathbb{CT}$ arriva in $\mathbb{TT}$ così come metà di quello che parte da $\mathbb{TT}$ arriva in $\mathbb{TC}$.
Sia da $\mathbb{TT}$ che da $\mathbb{CT}$ il processo appare come un ciclo semplice con $f_{\script u}\/=\/1/2$ e $f_{\script c}\/=\/1/2$: quello che cambia è la frequenza di ingresso

$f_{\script i,\mathbb{TT}}\/=\/\frac14\/+\/\frac18\/+\/\frac18\/+\/\frac18\/=\/\frac58$

($1/4$, ingresso diretto; $1/8$, ingresso da $\mathbb{CT}$, $\mathbb{CC}$ e $\mathbb{TC}$)

$f_{\script i,\mathbb{CT}}\/=\/\frac14\/+\/\frac14\/+\/\frac14\/+\/\frac18\/=\/\frac78$

($1/4$, ingresso diretto, da $\mathbb{CC}$ e da $\mathbb{TC}$; $1/8$, ingresso da $\mathbb{TT}$)

Evidentemente, essendo il resto uguale, gli odds sono: $\mathcal{O}_{\script 17}\/=\/5:7$.

Questo grafo ha anche un simmetrico: G35, $\mathbb{TCT}$ contro $\mathbb{CCC}$



i cui odds sono: $\mathcal{O}_{\script 35}\/=\/7:5$.

Altri sei grafi e abbiamo finito!

G23, $\mathbb{TTC}$ contro $\mathbb{TCT}$



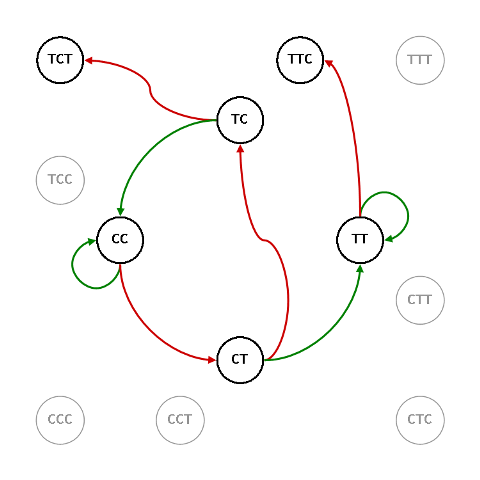
Da $\mathbb{TT}$ $f_{\script i}^{\script \prime}\/=\/\frac14\/+\/\frac14\/+\/\frac18\/=\/\frac12 \hspace{60} f_{\script c}^{\script \prime }\/=\/\frac14 \hspace{60} f_{\script u}^{\script \prime }\/=\/\frac12 \hspace{60} f_{\script e}\/=\/\frac14\/+\/\frac{\frac58\times\frac12}{1-\frac14}\/=\/\frac23$

Da $\mathbb{TC}$ $f_{\script i}\/=\/\frac14\/+\/\frac18\/+\/\frac18\/=\/\frac12 \hspace{60} f_{\script c}\/=\/\frac14 \hspace{60} f_{\script u}\/=\/\frac12 \hspace{60} f_{\script e}\/=\/\frac{\frac12\times\frac12}{1-\frac14}\/=\/\frac13$

Gli odds sono: $\mathcal{O}_{\script 23}\/=\/2:1$.

G24, $\mathbb{TTC}$ contro $\mathbb{TCC}$



Come per G14 La transizione $\left(\mathbb{CC}\right)_{\script n}\/\longrightarrow \/\mathbb{CT}$ è certa (in un numero incognito di passi) ragion per cui il grafo è equivalente al precedente con la sostituzione di

$\mathbb{TC}\/\longrightarrow \/\left(\mathbb{CC}\right)_{\script n}\/\longrightarrow \/\mathbb{CT}$

con

$\mathbb{TC}\/\longrightarrow \/\mathbb{CT}$

Gli odds sono: $\mathcal{O}_{\script 24}\/=\/2:1$.

Sotto $S_{\script 2$, a G23 corrisponde G67



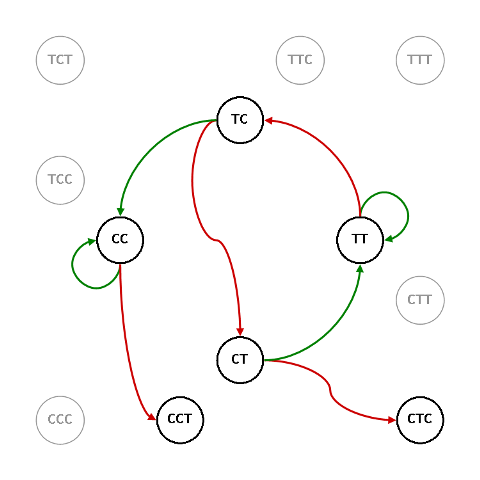
e a G24 corrisponde G68



Quindi, $\mathcal{O}_{\script 67}\/=\mathcal{O}_{\script 68}\/=\/2:1$.
 


G38, $\mathbb{TCT}$ contro $\mathbb{CTT}$



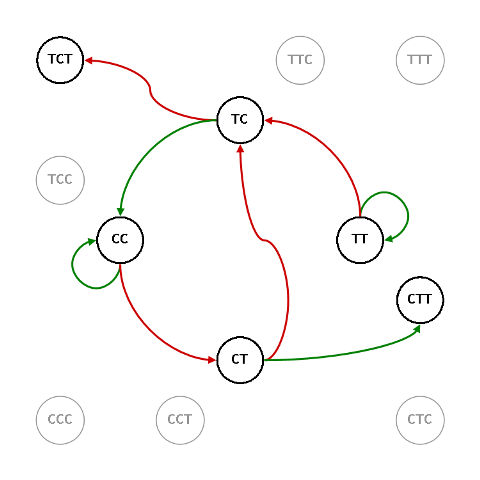
Questo grafo è pseudosimmetrico: la transizione

$\mathbb{TC}\/\longrightarrow \/\left(\mathbb{CC}\right)_{\script n}\/\longrightarrow \/\mathbb{CT}$

di questo grafo è equivalente alla transizione

$\mathbb{TC}\/\longrightarrow \/\mathbb{CT}$

di G48



e anche gli ingressi e uscite di $\mathbb{TC}$ e $\mathbb{CT}$ sono equivalenti
Gli odds sono: $\mathcal{O}_{\script 38}\/=\/1:1$.

Analoghe considerazioni valgono per il suo simmetrico G47, $\mathbb{TCC}$ contro $\mathbb{CTC}$



$\mathcal{O}_{\script 47}\/=\/1:1$.

Avendo esaurito tutte le possibilità ecco la tabella degli odds

$\begin{array}{cc}\begin{array}{c50|c50c50c50c50c50c50c50c50|C+50} & {\script \mathbb{TTT}} & {\script\mathbb{TTC}} & {\script\mathbb{TCT}} & {\script\mathbb{TCC}} & {\script\mathbb{CCC}} & {\script\mathbb{CCT}} & {\script\mathbb{CTC}} & {\script\mathbb{CTT}} & \\ \hline {\script\mathbb{TTT}} & \times & 1:1 & 2:3 & 2:3 & 1:1 & 3:7 & 5:7 & 1:7 \\ {\script \mathbb{TTC}} & 1:1 & \times & 2:1 & 2:1 & 7:3 & 1:1 & 5:3 & 1:3 \\ {\script \mathbb{TCT}} & 3:2 & 1:2 &\times & 1:1 & 7:5 & 3:5 & 1:1 & 1:1 \\ {\script\mathbb{TCC}} & 3:2 & 1:2 & 1:1 & \times & 7:1 & 3:1 & 1:1 & 1:1 \\ {\script\mathbb{CCC}} & 1:1 & 3:7 & 5:7 & 1:7 & \times & 1:1 & 2:3 & 2:3 \\ {\script\mathbb{CCT}} & 7:3 & 1:1 & 5:3 & 1:3 & 1:1 & \times & 2:2 & 2:1 \\ {\script\mathbb{CTC}} & 7:5 & 3:5 & 1:1 & 1:1 & 3:2 & 1:2 & \times & 1:1 \\ {\script\mathbb{CTT}} & 7:1 & 3:1 & 1:1 & 1:1 & 3:2 & 1:2 & 1:1 & \times \\ \hline\end{array} & \begin{array}{c80C+50} \\ 1:7 \\ 1:3 \\ 1:2 \\ 1:2 \\ 1:7 \\ 1:3 \\ 1:2 \\ 1:2 \end{array} \end{array}$

In colonna a destra è evidenziato il risultato peggiore per ogni scelta del primo giocatore: come si vede, il secondo può sempre ottenere una probabilità di vittoria maggiore di quella del primo.

[Pasquale]

Ciao grande Pan ! Esausto o esaustivo?

[panurgo]

Aspetta a vedere come funziona con tre o più giocatori...

[Pasquale]

....come immaginavo