panurgo ha scritto:La risposta è "Icosaedro", per la spiegazione dovrete attendere un pochino

Il tempo di scriverla in modo intelleggibile!
Non ci rimettiamo nulla a considerare, al posto dei nostri poliedri regolari, un generico dado a $n$ facce. Ovviamente, quella del dado è solo una metafora per una variabile casuale con distribuzione uniforme sugli $n$ valori ma continuiamo pure ad usarla, modificandola lievemente: anzichè numerare le facce del dado e poi lanciarlo, prima lo lanciamo e poi numeriamo la faccia su cui finisce per poggiare (naturamente se non è già numerata): quando numeriamo l’ultima faccia registriamo il numero $r$ ( $r\/>\/n$) di lanci che è stato necessario, cancelliamo i numeri dalle facce e ricominciamo.
Questo processo sembra fatto apposta per essere modellato con una catena di Markov del primo ordine: vi sono $n\/+\/1$ stati, corrispondenti ai possibili valori del numero di facce già numerate $k$, che vanno da $0$ a $n$; da ogni stato e possibile solo o passare allo stato successivo (ma non per lo stato $n$) o restare nello stesso stato (ma non per lo stato $0$).
Per assegnare le probabilità di transizione possiamo prescindere dalle problematiche legate al lancio del dado e usare invece il numero di facce segnate e non segnate
$\begin{array}{lC+50} p\left(k\/\rightarrow\/k\/\middle|\/n\/k\/I\right)\/=\/\frac k n \\ p\left(k\/\rightarrow\/k+1\/\middle|\/n\/k\/I\right)\/=\/\frac {n-k} n \end{array}$
La matrice di transizione è “bidiagonale” perché le transizioni avvengono soltanto tra stati “adiacenti”
$T\/=\/\frac1n\left(\begin{array}{c+40C+20} 0 & & & & & & & \\ n & 1 & & & & & & \\ & n-1 & 2 & & & & & \\ & & \ddots & \ddots & & & & \\ & & & n-i+1 & i & & & \\ & & & & \ddots & \ddots & & \\ & & & & & 2 & n-1 & \\ & & & & & & 1 & n \end{array}\right)$
Gli autovalori della matrice $T$, cioè le soluzioni dell’equazione determinantale
$\left|T\/-\/\lambda\/I\right|\/=\/0\/\qquad\Longrightarrow\qquad\prod_{\script k}\left(\frac kn\/-\/\lambda\right)\/=\/0$
sono gli elementi della diagonale principale, cioè $\lambda_{\script k}\/=\/\frac kn$.
Gli autovettori sono le soluzioni del sistema di equazioni lineari $\left(T\/-\/\lambda_{\script k}\/I\right)\/=\/0$: essi non cambiano se moltiplichiamo le equazioni per una costante quindi cercheremo le soluzioni del sistema $n\/\left(T\/-\/\lambda_{\script k}\/I\right)\/=\/\left(n\/T\/-\/k\/I\right)\/=\/0$, così avremo solo numeri interi.
Nota bene che faremo correre gli indici della matrice $S$ degli autovettori tra $0$ e $n$.
Scriviamo in modo esplicito il sistema per $k\/=\/0$
$\left\{\begin{array}{rc30l30C+30}0\cdot S_{\script 0,0}&=&0 \\n\cdot S_{\script 0,0}\/+\/1\cdot S_{\script 1,0}&=&0\\\left(n\/-\/1\right)\cdot S_{\script 1,0}\/+\/2\cdot S_{\script 2,0}&=&0\\&\vdots&\\\left(n\/-i\/+1\right) \cdot S_{\script i-1,0}\/+\/i\cdot S_{\script i,0}&=&0\\&\vdots&\\1\cdot S_{\script n-1,0}\/+\/n\cdot S_{\script n,0}&=&0\end{array}\right.$
Notiamo il termine generico, da cui ricaviamo
$S_{\script i,0}\/=\/-\frac{\left(n\/-i\/+1\right)}i\/S_{\script i-1,0}$
sostituendo all’indietro i valori di $S_{\script i-1,0}$, $S_{\script i-2,0}$ ecc.
$S_{\script i,0}\/=\/\left\[-\/\frac{\left(n-i+1\right)}{i}\right\]\/\times\/\left\[-\/\frac{\left(n-i+2\right)}{\left(i-1\right)}\right\]\/\times\/\dots\/\times\/\left\[-\/\frac{\left(n-1\right)}{2}\right\]\/\times\/\left\[-\/\frac{n}{1}\right\]\/ S_{\script 0,0}\/=\/\left(-1\right)^{\script i}\/{n \choose i}\/S_{\script 0,0}$
e ponendo convenientemente (vide infra) $S_{\script 0,0}\/=\/\left(-1\right)^{\script n}$ otteniamo
$S_{\script i,0}\/=\/\left(-1\right)^{\script n+i}\/{n \choose i}$
Scriviamo ora esplicitamente il sistema per $k\/=\/1$
$\left\{\begin{array}{rc30l30C+30}-\/1\cdot S_{\script 0,1}&=&0 \\n\cdot S_{\script 0,1}\/+\/0\cdot S_{\script 1,1}&=&0\\\left(n\/-\/1\right)\cdot S_{\script 1,1}\/+\/1\cdot S_{\script 2,1}&=&0\\&\vdots&\\\left(n\/-i\/+1\right) \cdot S_{\script i-1,1}\/+\/\left(i\/-\/1\right)\cdot S_{\script i,1}&=&0\\&\vdots&\\1\cdot S_{\script n-1,1}\/+\/\left(n\/-\/1\right)\cdot S_{\script n,1}&=&0\end{array}\right.$
dalla prima equazione ricaviamo che $S_{\script 0,1}\/=\/0$, col che il sistema diviene
$\left\{\begin{array}{rc30l30C+30}0\cdot S_{\script 1,1}&=&0\\\left(n\/-\/1\right)\cdot S_{\script 1,1}\/+\/1\cdot S_{\script 2,1}&=&0\\&\vdots&\\1\cdot S_{\script n-1,1}\/+\/\left(n\/-\/1\right)\cdot S_{\script n,1}&=&0\end{array}\right.$
dove adesso gli indici corrono da $1$ a $n$. Ma, ovviamente gli indici sono solo indici e se noi li diminuiamo di uno otteniamo
$\left\{\begin{array}{rc30l30C+30}0\cdot S_{\script 0,0}&=&0\\\left(n\/-\/1\right)\cdot S_{\script 0,0}\/+\/1\cdot S_{\script 1,0}&=&0\\&\vdots&\\1\cdot S_{\script n-2,0}\/+\/\left(n\/-\/1\right)\cdot S_{\script n-1,0}&=&0\end{array}\right.$
Cioè il primo autovettore della matrice di transizione per un dado con $n\/-\/1$ facce: data l’arbitrarietà di $n$, questo ragionamento prova che
$S\/=\/\left(\begin{array}{c+90C+40}\left(-1\right)^{\script n}{n \choose 0}&&&&& \\ \left(-1\right)^{\script n+1}{n \choose 1}&\left(-1\right)^{\script n+1}{n-1 \choose 0}&&&& \\ \vdots&\vdots&\ddots&&& \\ \left(-1\right)^{\script n+i}{n \choose i}&\left(-1\right)^{\script n+i}{n-1 \choose i-1}&\cdots&\left(-1\right)^{\script n+i}{n-j \choose i-j}&& \\ \vdots&\vdots&&\vdots&\ddots& \\ \left(-1\right)^{\script 2n}{n \choose n}&\left(-1\right)^{\script 2n}{n-1 \choose n-1}&\cdots&\left(-1\right)^{\script 2n}{n-j \choose n-j}&\cdots&\left(-1\right)^{\script 2n}{0 \choose 0} \end{array}\right)$
Seguendo la convenzione usuale che il coefficiente binomiale ${n \choose k}$ è nullo salvo che per $0\/\leq\/k\/\leq\/n$ indicheremo il termine generico di questa matrice come
$S_{\script i,j}\/=\left(-1\right)^{\script n+i}\/{n-j \choose i-j}$
Esempi di queste matrici sono
$\left(\begin{array}{r+20C+20}-1&0\\1&1\end{array}\right)\qquad\left(\begin{array}{r+20C+20}1&0&0\\-2&-1&0\\1&1&1\end{array}\right) \qquad\left(\begin{array}{r+20C+20}-1&0&0&0\\3&1&0&0\\-3&-2&-1&0\\1&1&1&1\end{array}\right) \qquad\left(\begin{array}{r+20C+20}1&0&0&0&0\\-4&-1&0&0&0\\6&3&1&0&0\\-4&-3&-2&-1&0\\1&1&1&1&1\end{array}\right) \qquad$
Motivo ora la scelta di porre $S_{\script 0,0}\/=\/\left(-1\right)^{\script n}$: la matrice che abbiamo ottenuto è autoinversa, cioè
$S^{\script -1}\/=\/S\qquad\Longleftrightarrow\qquad S^{\script 2}\/=\/I\qquad\Longleftrightarrow\qquad \sum_{\script k=0}^{\script n}{S_{\script i,k}\/S_{\script k,j}}\/=\/\delta_{\script i,j}$
dove $\delta_{\script i,j}$ è il delta di Kronecker che vale $1$ se $i\/=\/j$ mentre è nullo in caso contrario.
Per dimostrare che S è autoinversa consideriamo l’ultima relazione
$\sum_{\script k=0}^{\script n}{S_{\script i,k}\/S_{\script k,j}}\/=\/\sum_{\script k=0}^{\script n}\/\left(-\/1\right)^{\script n+i}\/{n-k \choose i-k}\/\left(-\/1\right)^{\script n+k}\/{n-j \choose k-j}\/=\/\sum_{\script k=0}^{\script n}\/\left(-\/1\right)^{\script i+k}\/{n-k \choose i-k}\/{n-j \choose k-j}\/=\/\delta_{\script i,j}$
Il termine della sommatoria è nullo a meno che sia $j\/\leq\/k\/\leq\/i$: espandendo e riarrangiando i coefficienti binomiali
${n-k \choose i-k}\/{n-j \choose k-j}\/=\/\frac{\cancel{\left(n-k\right)!}\left(n-j\right)!}{\left(i-k\right)!\left(n-i\right)!\left(k-j\right)!\cancel{\left(n-k\right)!}}\frac{\left(i-j\right)!}{\left(i-j\right)!}\/=\/\frac{\left(n-j\right)!\left(i-j\right)!}{\left(i-j\right)!\left(n-i\right)!\left(i-k\right)!\left(k-j\right)!}\/=\/{n-j \choose i-j}\/{i-j \choose i-k}$
otteniamo
$\sum_{\script k=0}^{\script n}{S_{\script i,k}\/S_{\script k,j}}\/=\/\left(-\/1\right)^{\script i-j}\/{n-j \choose i-j}\/\sum_{\script k=j}^{\script i}\left(-\/1\right)^{\script k+j}\/{i-j \choose i-k}$
E, ponendo $n\/-\/j\/=\/a$, $i\/-\/j\/=\/b$ e $k\/-\/j\/=\/c$,
$\sum_{\script k=0}^{\script n}{S_{\script i,k}\/S_{\script k,j}}\/=\/\left(-\/1\right)^{\script b}\/{a \choose b}\/\sum_{\script c=0}^{\script b}\left(-\/1\right)^{\script c}\/{b \choose c}$
Per $i\/=\/j$, cioè per $b\/=\/0$,
$\sum_{\script k=0}^{\script n}{S_{\script i,k}\/S_{\script k,j}}\/=\/\left(-\/1\right)^{\script 0}\/{a \choose 0}\/\left(-\/1\right)^{\script 0}\/{0 \choose 0}\/=\/1$
mentre, per $i\/>\/j$, la sommatoria è nulla per il teorema binomiale
$\sum_{\script c=0}^{\script b}\left(-\/1\right)^{\script c}\/{b \choose c}\/=\/\sum_{\script c=0}^{\script b}{b \choose c}\/\left(-\/1\right)^{\script c}\/\left(1\right)^{\script b-c}\/=\/\left(1\/-\/1\right)^{\script b}\/=\/0$
Ma perché ci danniamo tanto l’anima per trovare autovalori e autovettori di $T$?
La matrice degli autovettori, quando è invertibile, consente di diagonalizzare la matrice $T$
$S\/T\/S^{\script -1}\/=\/S\/T\/S\/=\/\Lambda\/=\/{\text diag}\left\{\lambda_{\script k}\right\}$
(il primo passaggio è giustificato dal fatto che $S$ è autoinversa)
Bene! E allora?
Si può anche fare il contrario
$S\;{\text diag}\left\{\lambda_{\script k}\right\}\/S\/=\/S\/\Lambda\/S\/=\/T$
No, non vi prendo in giro: le potenze di una matrice diagonale si calcolano elevando a potenza gli elementi della diagonale quindi è
$S\;{\text diag}\left\{\lambda_{\script k}^{\script r}\right\}\/S\/=\/S\/\Lambda^{\script r}\/S\/=\/T^{\script r}$
e a noi serve proprio $T^{\script r}$.
La matrice di transizione di una catena di Markov raccoglie le probabilità di transizione in un passo; $T^{\script 2}$ contiene le probabilità di transizione in due passi, $T^{\script 3}$ quelle in tre e così via.
$T^{\script r}$ contiene dunque le probabilità di transizione in $r$ passi, giusto quello che ci serve per calcolare l’expectation del nostro giochino.
Ma vediamo meglio: la transizione che ci interessa è quella dallo stato $0$ allo stato $n$ e cioè l’elemento $T_{\script n,0}^{\script r}$
$T_{\script n,0}^{\script r}\/=\/\sum_{\script k=0}^{\script n}S_{\script n,k}\/\lambda_{\script k}^{\script r}\/S_{\script k,0}\/=\/\sum_{\script k=0}^{\script n}1\/\times\left(\frac kn\right)^{\script r}\/\times\/\left(-\/1\right)^{\script n+k}\/{n \choose k}$
Si tratta di una distribuzione cumulativa di probabilità, cioè la probabilità di essere arrivati nello stato $n$ in al più $r$ passi.
$F\left(r\/\middle|\/n\/I\right)\/=\/\left\{\begin{array}{l+160C+40}0&r\/<\/n\\\sum_{\script k=0}^{\script n}\left(-1\right)^{\script n+k}\/{n \choose k}\/\left(\frac kn\right)^{\script r}&r\/\geq\/n\end{array}\right.$
Discutiamo questo concetto considerando, per semplicità, un dado a due facce: ecco la rappresentazione grafica del processo
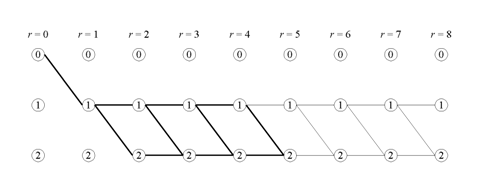
Dovrebbe essere chiaro che, se al quinto passo sono nello stato $2$ ci posso essere arrivato attraverso uno qualunque dei percorsi evidenziati (voi mi direte che dovevamo fermarci una volta numerato tutto il dado, ma la matrice di transizione mica lo sa

): la probabilità di esserci arrivato esattamente al quinto passo è $F\left(r=5\/\middle|\/2\/I\right)\/-\/F\left(r=4\/\middle|\/2\/I\right)$.
In generale
$p\left(r\/\middle|\/n\/I\right)\/=\/F\left(r\/\middle|\/n\/I\right)\/-\/F\left(r-1\/\middle|\/n\/I\right)\/=\/\left\{\begin{array}{l+240C+40}0&r\/<\/n\\\sum_{\script k=0}^{\script n}\left(-1\right)^{\script n+k+1}\/{n \choose k}\/\left(1\/-\/\frac kn\right)\/\left(\frac kn\right)^{\script r-1}&r\/\geq\/n\end{array}\right.$
Notiamo anche che il termine della sommatoria, $\left(-1\right)^{\script n+k+1}\/{n \choose k}\/\left(1\/-\/\frac kn\right)\/\left(\frac kn\right)^{\script r-1}$, si annulla per $k\/=\/0$ e per $k\/=\/n$.
Calcoliamo ora l’expectation di $r$
$\left\langle r\/\middle|\/n\/I\right\rangle\/=\/\sum_{\script r=0}^{\script\infty}r\/p\left(r\/\middle|\/n\/I\right)\/=\/\sum_{\script r=n}^{\script\infty} \sum_{\script k=1}^{\script n-1}\left(-1\right)^{\script n+k+1}\/{n \choose k}\/\left(1\/-\/\frac kn\right)\;r\/\left(\frac kn\right)^{\script r-1}$
Poniamo $q_{\script k}\/=\/\frac kn$ e invertiamo l’ordine delle due sommatorie
$\left\langle r\/\middle|\/n\/I\right\rangle\/=\/\sum_{\script k=1}^{\script n-1}\left(-1\right)^{\script n+k+1}\/{n \choose k}\/\left(1\/-\/q_{\script k}\right)\; \sum_{\script r=n}^{\script\infty}r\/q_{\script k}^{\script r-1}$
Affrontiamo per prima la sommatoria interna: osserviamo che $r\/q_{\script k}^{\script r-1}\/=\/\frac d{dq_{\script k}}\/q_{\script k}^{\script r}$ e quindi
$\begin{array}{lC+60}\sum_{\script r=n}^{\script \infty}{r\/q_{\script k}^{\script r-1}}\/=\/\sum_{\script r=0}^{\script \infty}{r\/q_{\script k}^{\script r-1}}\/-\/\sum_{\script r=0}^{\script n-1}{r\/q_{\script k}^{\script r-1}}\/=\/\frac d{dq_{\script k}}\/\left\[\sum_{\script r=0}^{\script \infty}{q_{\script k}^{\script r}}\/-\/\sum_{\script r=0}^{\script n-1}{q_{\script k}^{\script r}}\right\]\/=\/\\\hspace{80}=\/\frac d{dq_{\script k}}\/\left\[\frac 1{1- q_{\script k}}\/-\/\frac {1- q_{\script k}^{\script n}}{1- q_{\script k}}\right\]\/=\/\frac d{dq_{\script k}}\/\frac {q_{\script k}^{\script n}}{1- q_{\script k}}\/=\/\frac{n\/ q_{\script k}^{\script n-1}-\left(n-1\right) q_{\script k}^{\script n}}{\left(1- q_{\script k}\right)^{\script 2}}\/=\/\frac{n^{\script 2}\/k^{\script n-1}\/-\/\left(n-1\right)\/k^{\script n}}{\left(n-k\right)\/n^{\script n-1}}\end{array}$
Sostituiamo questa espressione nel calcolo dell’expectation
$\left\langle r\/\middle|\/n\/I\right\rangle\/=\/\sum_{\script k=1}^{\script n-1}\left(-1\right)^{\script n+k+1}\/{n \choose k}\/\left(1\/-\/q_{\script k}\right)\; \frac{n^{\script 2}\/k^{\script n-1}\/-\/\left(n-1\right)\/k^{\script n}}{\left(n-k\right)\/n^{\script n-1}}$
e qui ci fermiamo lasciando al computer il compito di calcolare
$\begin{array}{lC+40}\left\langle r\/\middle|\/4\/I\right\rangle\/=\/\frac{25}{3}\/=\/8,33\ldots \\ \left\langle r\/\middle|\/6\/I\right\rangle\/=\/\frac{147}{10}\/=\/14,7 \\ \left\langle r\/\middle|\/8\/I\right\rangle\/=\/\frac{761}{35}\/=\/21,7\ldots \\ \left\langle r\/\middle|\/12\/I\right\rangle\/=\/\frac{86021}{2310}\/=\/37,2\ldots \\ \left\langle r\/\middle|\/20\/I\right\rangle\/=\/\frac{279175675}{3879876}\/=\/71,9\ldots \end{array}$
Icosaedro!



