Pagina 1 di 1
Quadrilatero ed angoli
Inviato: sab ott 15, 2011 5:55 pm
da karl
Sia ABCD un quadrilatero con l'angolo CBD doppio dell'angolo ADB e l'angolo ABD doppio dell'angolo CDB.Sapendo che AB=CB dimostrare che è pure AD=CD .
Re: Quadrilatero ed angoli
Inviato: dom ott 16, 2011 3:14 pm
da Info
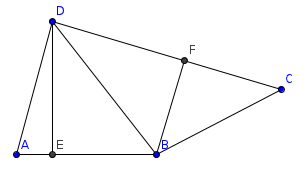
- quadrilatero.png (8.21 KiB) Visto 7496 volte
partiamo con le relazioni fra gli angoli e i lati
CBD=2ADB
ABD=2CDB
AB=CB
parto con il triangolo in basso
$BE=DB\cdot\cos\(ABD\)=DB\cdot\cos\(2\cdot CDB\)$
$DAB=\pi-ADB-ABD\\AE=AD\cdot\cos\(DAB\)=AD\cdot\cos\(\pi-\(ADB+ABD\)\)=\\
AD\cdot\(\cos\(\pi\)\cdot\cos\(ADB+ABD\)+\sin\(\pi\)\cdot\sin\(ADB+ABD\)\)=
-AD\cdot\cos\(ADB+ABD\)=-AD\cdot\cos\(\frac{CBD}2+2\cdot CDB\)$
trovo anche BE
$BE=DB\cdot\cos\(2\cdot CDB\)\\AE=-AD\cdot\cos\(\frac{CBD}2+2\cdot CDB\)\\AB=AE+BE=DB\cdot\cos\(2\cdot CDB\)-AD\cos\(\frac{CBD}2+2\cdot CDB\)$
mi sposto sull'altro triangolo
$DF=DB\cdot\cos\(CDB\)$
$BCD=\pi-CBD-CDB\\CF=CB\cdot\cos\(BCD\)=CB\cdot\cos\(\pi-CBD-CDB\)=-CB\cdot\cos\(CBD+CDB\)$
$CD=CF+DF=DB\cdot\cos\(CDB\)-CB\cdot\cos\(CBD+CDB\)$
ma CB=AB quindi
$CD=DB\cdot\cos\(CDB\)-\(DB\cdot\cos\(2\cdot CDB\)-AD\cdot\cos\(\frac{CBD}2+2\cdot CDB\)\)$
ma DB devo sostituirlo in funzione dei lati che conosco
$\frac{DB}{\sin\(DAB\)}=\frac{AD}{\sin\(ABD\)}\\DB=\frac{AD\cdot\sin\(DAB\)}{\sin\(ABD\)}\\DAB=\pi-ADB-ABD\\DB=\frac{AD\cdot\sin\(DAB\)}{\sin\(ABD\)}=AD\cdot\sin\(\pi\)\cdot\cos\(ADB+ABD\)-AD\cdot\cos\(\pi\)\cdot\sin\(ADB+ABD\)\\DB=AD\cdot\sin\(ADB+ABD\)=AD\cdot\sin\(\frac{CBD}2+2\cdot CDB\)$
passo a CD
$CD=DB\cdot\cos\(CDB\)-DB\cdot\cos\(2\cdot CDB\)-AD\cdot\cos\(\frac{CBD}2+2\cdot CDB\)\\CD=AD\cdot\sin(\frac{CBD}2+2\cdot CDB\)-\(AD\cdot\sin\(\frac{CBD}2+2\cdot CDB\)\cdot\cos\(2\cdot CDB\)-AD\cdot\cos\(\frac{CBD}2+2\cdot CDB\)\)$
ma CD=AD.... verifichiamo
$CD=CD\cdot\sin\(\frac{CBD}2+2\cdot CDB\)-\(CD\cdot sin\(\frac{CBD}2+2\cdot CDB\)\cdot\cos\(2\cdot CDB\)-CD\cdot\cos\(\frac{CBD}2+2\cdot CDB\)\)=\\CD\cdot\sin\(\frac{CBD}2+2\cdot CDB\)-CD\(\sin\(\frac{CBD}2+2\cdot CDB\)\cdot\cos\(2\cdot CDB\)-\cos\(\frac{CBD}2+2\cdot CDB\)\)$
quindi
$CD=CD\cdot\sin\(\frac{CBD}2+2\cdot CDB\)-CD\cdot\(\sin\(\frac{CBD}2+2\cdot CDB\)\cdot\cos\(2\cdot CDB\)-\cos\(\frac{CBD}2+2\cdot CDB\)\)\\1=\sin\(\frac{CBD}2+2\cdot CDB\)-\sin\(\frac{CBD}2+2\cdot CDB\)\cdot\cos\(2\cdot CDB\)+\cos\(\frac{CBD}2+2\cdot CDB\)$
stasera provero`a concludere i calcoli per verificare l'indentita`
Re: Quadrilatero ed angoli
Inviato: lun ott 17, 2011 11:20 am
da Ivana
Credo che,
per costruzione, nel rispetto dei dati del problema, risulti possibile soltanto l'aquilone...
Ecco, in allegato, un esempio di aquilone... Arrotondamento: 1 cifra decimale
Lascio ad altri la dimostrazione di questo problema di geometria sintetica

Re: Quadrilatero ed angoli
Inviato: lun ott 17, 2011 12:32 pm
da panurgo
Ivana ha scritto:Credo che,
per costruzione, nel rispetto dei dati del problema, risulti possibile soltanto l'aquilone...
Ecco, in allegato, un esempio di aquilone... Arrotondamento: 1 cifra decimale
Lascio ad altri la dimostrazione di questo problema di geometria sintetica

Avresti dovuto scrivere:
E' intuitivamente chiaro che, per costruzione e nel rispetto dei dati del problema, risulta possibile soltanto l'aquilone...

continua...
Re: Quadrilatero ed angoli
Inviato: lun ott 17, 2011 1:16 pm
da Ivana
panurgo ha scritto:Ivana ha scritto:Credo che,
per costruzione, nel rispetto dei dati del problema, risulti possibile soltanto l'aquilone...
Ecco, in allegato, un esempio di aquilone... Arrotondamento: 1 cifra decimale
Lascio ad altri la dimostrazione di questo problema di geometria sintetica

Avresti dovuto scrivere:
E' intuitivamente chiaro che, per costruzione e nel rispetto dei dati del problema, risulta possibile soltanto l'aquilone...

continua...
"È intuitivamente chiaro"
per chi?  Per te sicuramente, non ho dubbi
Per te sicuramente, non ho dubbi,

ma...
"è intuitivamente chiaro" anche per qualunque lettore di questo problema? 

Re: Quadrilatero ed angoli
Inviato: lun ott 17, 2011 8:28 pm
da panurgo
La locuzione
è intuitivamente chiaro o
è intuitivamente ovvio è spesso usata da voi matematici nei casi in cui sapete bene che le cose stanno così ma non vi riesce di trovare una dimostrazione: anche a noi matefili succede la stessa cosa.

Proviamo un po' a costruire questo mal... benedetto quadrilatero
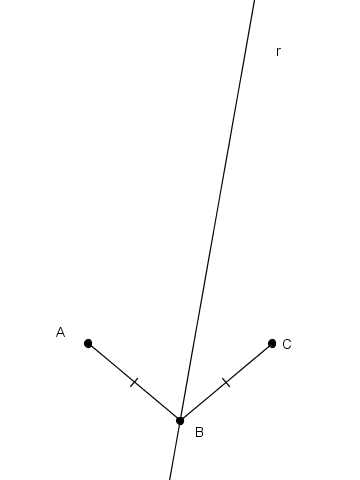
I lati $\overline{\text AB}$ e $\overline{\text BC}$ sono congruenti, l'angolo in $B$ è di $100^{\circ}$ (un valore qualsiasi) e la retta $r$ passa per $\text B$
dividendo l'angolo in due parti disuguali.
Tracciamo la bisettrice dell'angolo alla sinistra di $r$, la parallela ad essa passante per $\text C$

ed individuiamo il punto ${\text D}_{\script 1}$: chiaramente abbiamo $\angle\/{ABD}_{\script 1}\/=\/2\/\eta$
Ripetiamo il giochino per l'angolo a destra di $r$

e individuiamo il punto ${\text D}_{\script 2}$ con $\angle\/{CBD}_{\script 2}\/=\/2\/\zeta$
Se ora cambiamo la pendenza della retta $r$, per esempio così

dovrebbe essere divenuto
intuitivamente chiaro che, per ragioni di simmetria, l'unico modo di avere il segmento ${\text AD}_{\script 2}$ congruente con il segmento ${\text CD}_{\script 1}$ sia di avere $\eta\/=\/\zeta$
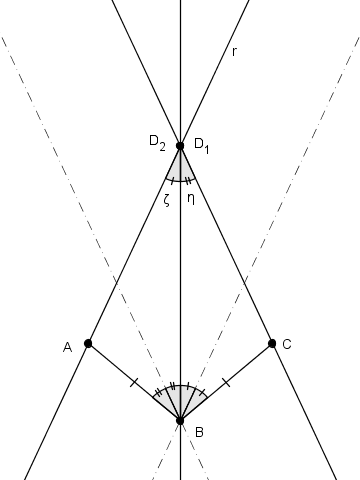
cioè il beneamato "aquilone".

P.S.: Si potrebbe forse sfruttare il fatto che, in un triangolo, all'angolo maggiore corrisponde il lato maggiore e viceversa, tenuto conto che i due triangoli hanno i lati $\overline{\text AB}$ e $\overline{\text BC}$ congruenti e che uno dei due angoli non può crescere senza che diminuisca l'altro...
Re: Quadrilatero ed angoli
Inviato: mar ott 18, 2011 7:38 am
da Ivana
Pan, credo che, almeno per molti matematici, tutto sia ovvio soltanto…dopo…
Ad esempio, in base dieci, 12+2=14, ma nell’aritmetica wittgensteiniana risulta che 12+2=15.
Come ci riferisce Hersh nel libro Cos’è davvero la matematica, Russell fu il mentore di Wittgenstein, ma Wittgenstein diceva che Russell non capiva il suo Tractatus. E, inoltre, Russell stesso ha detto (scrivo “ha detto”e non “disse”, perché reputo la sua affermazione ancora attualmente significativa e valida):
La matematica è la sola scienza esatta in cui non si sa mai di cosa si sta parlando, né se quello che si dice è vero.
Mi sembra (se non ricordo male!) che Russell abbia sostenuto anche che sia bene mettere un punto interrogativo a ciò che a lungo è stato dato per scontato…
Re: Quadrilatero ed angoli
Inviato: mar ott 18, 2011 12:53 pm
da panurgo
panurgo ha scritto:P.S.: Si potrebbe forse sfruttare il fatto che, in un triangolo, all'angolo maggiore corrisponde il lato maggiore e viceversa, tenuto conto che i due triangoli hanno i lati $\overline{\text AB}$ e $\overline{\text BC}$ congruenti e che uno dei due angoli non può crescere senza che diminuisca l'altro...
Vediamo se può funzionare...
Supponiamo di costruire il nostro aquilone
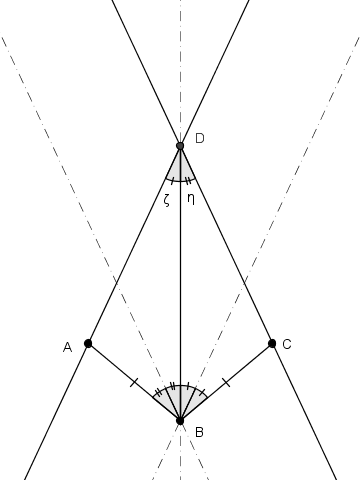
La condizione $\eta\/=\/\zeta$ è sufficiente.
Se la retta $r$ non è la bisettrice dell'angolo in $\text B$ allora i lati ${\text AD}$ e ${\text CD}$ non possono essere congruenti

Infatti, i due triangoli $\triangle {\text ABD}_{\script 1}$ e $\triangle {\text BCD}_{\script 1}$ hanno obbligatoriamente due lati congruenti (il lato ${\text BD}_{\script 1}$ è in comune e ${\text AB}$ e ${\text BC}$ lo sono per ipotesi) e l'angolo compreso diverso (altrimenti si torna all'aquilone). Quindi, per il primo criterio di congruenza, i due triangoli
NON sono congruenti.
La condizione $\eta\/=\/\zeta$ è anche necessaria.
QED
Non so se vi accade lo stesso ma tutto ciò, se è una dimostrazione, mi è
intuitivamente molto meno chiaro...
Re: Quadrilatero ed angoli
Inviato: mar ott 18, 2011 2:24 pm
da Ivana
Non so se possa bastare la "dimostrazione per costruzione"...
Inoltre, poiché alla parola "aquilone" si associa spesso solo la figura convessa specifica, ritengo opportuno aggiungere che potrebbe trattarsi anche di un aquilone concavo detto "punta", o "dardo", ma anche per il dardo non saprei andare oltre la "dimostrazione per costruzione"...

Ecco un esempio grafico. Arrotondamento: due cifre decimali
Re: Quadrilatero ed angoli
Inviato: mar ott 18, 2011 9:27 pm
da fabtor
Stavo provando ad immaginare le possibili soluzioni se si considerasse un piano ellittico, ma dopo aver scritto un post fiume a riguardo mi sono reso conto che ciò che avevo concluso non aveva alcun senso, quindi provo a girare a voi la domanda (non so perchè, ma ho come la sensazione che in questo piano il range di possibili forme possa essere più ampio).
Solo una domanda: e se lo costruissimo direttamente come riflessione di un triangolo rettangolo 30/60 lungo la sua ipotenusa (x poi magari generalizzare a tutti gli altri che rispettano la condizione data degli angoli uno doppio dell'altro) la cosa non potrebbe aiutare?






