Ciao a tutti,
Improvvisamente, il 28 giugno (6-28), la Grande Ragnatela si è riempita di titoli inquietanti:
Pi Greco sarebbe andato in pensione o forse morto, ma ancora peggio, sarebbe sbagliato.
Il suo successore sarebbe Tau:
$\Large \tau=2\pi$
I motivi di questa proposta si trovano nel "The Tau Manifesto" di Michael Hartl (http://tauday.com/pdf).
Due motivazioni che mi hanno colpito, una a favore e una contraria.
A favore:
$\Large e^{i\tau}=1$
Contraria:
$\Large \pi=\frac{\mbox{circonferenza}}{\mbox{diametro}}$
$\Large \tau=\frac{\mbox{circonferenza}}{\mbox{raggio}}$
Ma la circonferenza è "più" legata al suo diametro che al suo raggio.
Infatti se disegno un raggio sul piano voi non potete sapere con certezza qual è la sua circonferenza (ce ne sono due), se invece disegno un diametro voi potete trovare con certezza qual è la sua circonferenza!
Dal punto di vista matematico, usare Tau o Pi è sostanzialmente la stessa cosa.
Ma dal punto di vista filosofico, pratico e didattico, che cosa ne pensate?
E' meglio Tau o Pi?
Gianfranco
Tau contro Pi
Moderatori: Gianfranco, Bruno
Questo forum è una sezione del PORTALE DI BASE CINQUE
-
Gianfranco
- Supervisore del sito

- Messaggi: 1828
- Iscritto il: ven mag 20, 2005 9:51 pm
- Località: Sestri Levante
- Contatta:
Tau contro Pi
Pace e bene a tutti.
Gianfranco
Gianfranco
Re: Tau contro Pi
Se interpreto bene le varie fonti il successore di $\pi$ sarebbe $\tau$ con $\pi\/=\/\tau/2$!Gianfranco ha scritto:Il suo successore sarebbe Tau: $\Large \tau=2\pi$
La motivazione che più mi ha colpito è esplicitata in questa figura e l'immediatezza che ne deriva quando si trattano i radianti...
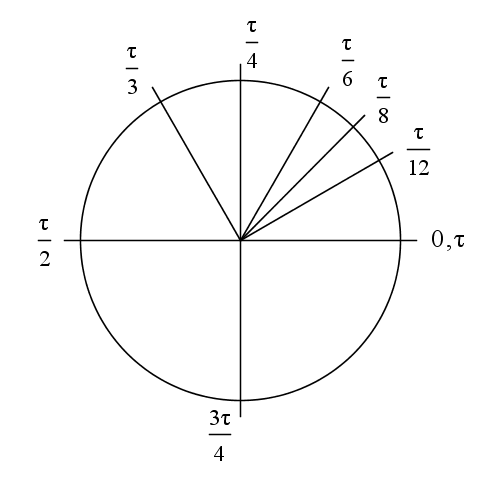
il panurgo
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
-
Gianfranco
- Supervisore del sito

- Messaggi: 1828
- Iscritto il: ven mag 20, 2005 9:51 pm
- Località: Sestri Levante
- Contatta:
Re: Tau contro Pi
Ciao Panurgo,
concordo: anche quella che hai citato tu è una ottima motivazione.
Nella mia scala sta ai primissimi posti, forse al secondo, sopratutto per motivi didattici.
Non riesco ad afferrare che differenza c'é fra dire:
"Il suo (di pi) successore sarebbe Tau: tau = 2 pi"
e
"Il successore di pi sarebbe tau, con pi = tau/2"
Ciao e buone vacanze a tutti!
Gianfranco
concordo: anche quella che hai citato tu è una ottima motivazione.
Nella mia scala sta ai primissimi posti, forse al secondo, sopratutto per motivi didattici.
Non riesco ad afferrare che differenza c'é fra dire:
"Il suo (di pi) successore sarebbe Tau: tau = 2 pi"
e
"Il successore di pi sarebbe tau, con pi = tau/2"
Ciao e buone vacanze a tutti!
Gianfranco
Pace e bene a tutti.
Gianfranco
Gianfranco
Re: Tau contro Pi
era soltanto una battuta: infatti i $\tau$-isti considerano $\pi$ come derivato... 
il panurgo
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
-
Gianfranco
- Supervisore del sito

- Messaggi: 1828
- Iscritto il: ven mag 20, 2005 9:51 pm
- Località: Sestri Levante
- Contatta:
Re: Tau contro Pi
Ciao Panurgo,
Giusto, e la differenza non è neanche tanto sottile.
Posso accettare (ma non sono ancora convinto) di usare tau al posto di 2pi in molti contesti ma non mi sento di gettare pi nel fango cancellando millenni di storia.
Nella mia conformazione mentale, tau deriva da pi.
Ma posso allenarmi e cambiare punto di vista. Inoltre basta una nuova generazione di studenti per dimenticare completamente il passato (su una cosa così semplice).
Però mi è venuta una curiosità: qual è la storia di pi? Perché nella geometria, nella trigonometria, nell'analisi, nella fisica, tutti hanno continuato a usare 2pi invece di istituire una nuova costante? Qualche motivo ci deve essere!
Ciao
Gianfranco
Giusto, e la differenza non è neanche tanto sottile.
Posso accettare (ma non sono ancora convinto) di usare tau al posto di 2pi in molti contesti ma non mi sento di gettare pi nel fango cancellando millenni di storia.
Nella mia conformazione mentale, tau deriva da pi.
Ma posso allenarmi e cambiare punto di vista. Inoltre basta una nuova generazione di studenti per dimenticare completamente il passato (su una cosa così semplice).
Però mi è venuta una curiosità: qual è la storia di pi? Perché nella geometria, nella trigonometria, nell'analisi, nella fisica, tutti hanno continuato a usare 2pi invece di istituire una nuova costante? Qualche motivo ci deve essere!
Ciao
Gianfranco
Pace e bene a tutti.
Gianfranco
Gianfranco
Re: Tau contro Pi
Si, basterebbe una generazione di studenti, ma ammesso fosse possibile organizzate tutte le scuole del mondo o di una buona fetta di esso in contemporanea (con una organizzazione mondiale che letteralmente imponga tau al posto di pi!?), come la mettiamo con la sterminata letteratura matematica degli ultimi due millenni e passa? Cambiare pi con tau non è come declassare Plutone da pianeta di serie A a pianeta di serie B.
La matematica non è solo eleganza formale, ma è anche e soprattutto tradizione.
C'è un bellissimo lavoro su Matematicamente.it, e cioè il testo per le superiori creato con licenza aperta Creative Commons. Ebbene, anche lì si continua ad usare la convenzione (a mio giudizio antipaticissima!) di denominare il perimetro delle figure piane con il simbolo 2p, così il semiperimetro (dicono!) è più comodo da scrivere. La trovo una cosa molto sciocca, ma non mi sognerei di dire ai miei studenti che il perimentro si indica con la "p", poiché li getterei nella confusione.
O no?
La matematica non è solo eleganza formale, ma è anche e soprattutto tradizione.
C'è un bellissimo lavoro su Matematicamente.it, e cioè il testo per le superiori creato con licenza aperta Creative Commons. Ebbene, anche lì si continua ad usare la convenzione (a mio giudizio antipaticissima!) di denominare il perimetro delle figure piane con il simbolo 2p, così il semiperimetro (dicono!) è più comodo da scrivere. La trovo una cosa molto sciocca, ma non mi sognerei di dire ai miei studenti che il perimentro si indica con la "p", poiché li getterei nella confusione.
O no?
Ogni limite ha una pazienza! (Totò)
Re: Tau contro Pi
La storia del perimetro segnato come "2p" è una sorta di ciclo e riciclo storico!!! Personalmente lo trovo antipatico anch'io (anche perchè la giustificazione data del semiperimetro mi sembra un po' una sciocchezza visto le "molteplici" aplicazioni del semiperimetro!!!!) tuttavia, molti libri di testo delle medie (forse per risparmiare inchiostroantonio ha scritto:Si, basterebbe una generazione di studenti, ma ammesso fosse possibile organizzate tutte le scuole del mondo o di una buona fetta di esso in contemporanea (con una organizzazione mondiale che letteralmente imponga tau al posto di pi!?), come la mettiamo con la sterminata letteratura matematica degli ultimi due millenni e passa? Cambiare pi con tau non è come declassare Plutone da pianeta di serie A a pianeta di serie B.
La matematica non è solo eleganza formale, ma è anche e soprattutto tradizione.
C'è un bellissimo lavoro su Matematicamente.it, e cioè il testo per le superiori creato con licenza aperta Creative Commons. Ebbene, anche lì si continua ad usare la convenzione (a mio giudizio antipaticissima!) di denominare il perimetro delle figure piane con il simbolo 2p, così il semiperimetro (dicono!) è più comodo da scrivere. La trovo una cosa molto sciocca, ma non mi sognerei di dire ai miei studenti che il perimentro si indica con la "p", poiché li getterei nella confusione.
O no?
Per quanto riguarda l'utilizzo del Tau al posto di pigreca, sarà che sono vecchio stampo, ma la cosa non mi sconfinfera proprio: per me Tau resta il numero della sezione aurea!
A proposito lo sapevate che un triangolo scaleno che a per lati minori il numero di eulero e il numero della sezione aurea e per lato maggiore pigreca è quasi un triangolo rettangolo?
In geometria euclidea il fatto che sia acutangolo è abbastanza semplice da dimostrare per approssimazione.
Qualcuno di voi saprebbe dimostrare se nella geometria ellittica tale triangolo potrebbe effettivamente essere rettangolo o meno? In caso affermativo la cosa per quanto mi riguarda avrebbe un certo fascino...
Ah, se i portieri avessero sulla maglia: $|e^{-i\pi}|$...
Pongo $y = x^{2}$ quindi $y=\frac {x^{2}}{pongo}$
[tratto da un compito in classe di uno studente di prima superiore]
Il vero gnomone aureo: http://thumbs.dreamstime.com/z/gnomo-de ... 526933.jpg
Pongo $y = x^{2}$ quindi $y=\frac {x^{2}}{pongo}$
[tratto da un compito in classe di uno studente di prima superiore]
Il vero gnomone aureo: http://thumbs.dreamstime.com/z/gnomo-de ... 526933.jpg



