Un pedone a passeggio

[franco]

Abbiamo un pedone in una scacchiera di dimensioni infinite che può muoversi ogni volta di un solo passo in avanti, indietro, destra o sinistra.
Le quattro direzioni sono equiprobabili e nulla osta che il pedone torni in caselle occupate in precedenza.

Le domande, tratte dal solito sito Francese sul quale vado a curiosare ogni tanto, sono le seguenti:
Qual'è la probabilità che, dopo dieci mosse, il pedone si trovi ...
1 ... nella stessa casella dalla quale era partito?
2 ... all'interno di un quadrato 5x5 il cui centro coincide con la casella di partenza?
3 ... all'interno di una croce con centro nella casella di partenza e "braccia" lunghe 10 caselle?


---------------------------------------

P.S. (offtopic)
Qualcuno sa come mai, da quanto sono passato al browser Firefox, non riesco più a loggarmi al forum?
Mi viene chiesta username e password, il sistema mi propone di memorizzarla, ma che io risponda Si o No il risultato è sempre una nuova richiesta di inserimento username e password.
Alla fine, per riuscire ad entrare, sono dovuto ripassare ad Explorer!

ciao

[Info]

ciao, ti ho risposto in privato per quanto riguarda l'off-topic

[0-§]

La prima è la più semplice e SE&O la risposta dovrebbe essere

3969/65536, cioè circa 0.06

Una veloce simulazione al computer conferma il risultato teorico: se conferma anche franco stasera posto la mia soluzione.
Stay tuned!
0-§

[David]

Mi viene da dire per la prima domanda

p=((9!/(4!5!0!0!)) + (9!/(3!4!1!1!)) + (9!/(2!3!2!2!)) + (9!/(1!2!3!3!)) + (9!/(0!1!4!4!)))*((1/4)^9)=3969/65536

leggermente più del 6%

[0-§]

Mi viene da dire per la prima domanda

p=((9!/(4!5!0!0!)) + (9!/(3!4!1!1!)) + (9!/(2!3!2!2!)) + (9!/(1!2!3!3!)) + (9!/(0!1!4!4!)))*((1/4)^9)=3969/65536

leggermente più del 6%

Oh yes! (un basecinquino può sbagliare, due no!)

Nel frattempo mi sono buttato anche sulla seconda, ottenendo

4473/8192: poco più di 0,546

Anche qui "la macchina" conferma; la mia soluzione tuttavia è assai brutta e calcolosa, sicchè sospetto che ce ne sia un'altra, molto più diretta, di cui tanto per cambiare non mi sono reso conto.
Aspetto dunque a postare, per vedere se come al solito ho usato più la penna che l'astuzia e se qualcuno riesce a risolvere la questione in maniera più semplice.
Buona serata a tutti,
0-§

[David]

Per la terza domanda non ho trovato di meglio che:

p(3)=
2*((1/4)^9)*((9!/(9!0!0!0!))+ (9!/(8!1!0!0!)) + (9!/(7!2!0!0!)) + (9!/(6!3!0!0!))+ (9!/(5!4!0!0!)+ (9!/(7!0!1!1!) )+ (9!/(6!1!1!1!)) +
+(9!/(5!2!1!1!)+ (9!/(4!3!1!1!))+ (9!/(5!0!2!2!))+ (9!/(4!1!2!2!))+ (9!/(3!2!2!2!)) + (9!/(3!0!3!3!))+ (9!/(2!1!3!3!))+(9!/1!0!4!4!)))=
=12155/65536

circa 18.5%

Ciao

[0-§]

12155/65536

Dissento. A me viene infatti 76501/262144, cioè circa il 29,18%.
David, non mi è chiaro il tuo metodo; puoi spiegarti?

Bye
ZF

[David]

Dissento pure io dalla... mia risposta,avendo considerato solo 2 braccia della croce.

Dovrò rifare i calcoli ma presumo il tuo valore sia quello giusto.

Au revoir

[David]

Ho rifatto e allora:




p(3)=
2*((1/4)^9)*((9!/(9!0!0!0!))+ (9!/(8!1!0!0!)) + (9!/(7!2!0!0!)) + (9!/(6!3!0!0!))+ (9!/(5!4!0!0!)+ (9!/(7!0!1!1!) )+ (9!/(6!1!1!1!)) +
+(9!/(5!2!1!1!)+ (9!/(4!3!1!1!))+ (9!/(5!0!2!2!))+ (9!/(4!1!2!2!))+ (9!/(3!2!2!2!)) + (9!/(3!0!3!3!))+ (9!/(2!1!3!3!))+(9!/(1!0!4!4!))+
+(9!/(3!4!2!0!)) + (9!/(2!3!4!0!)) + (9!/(2!3!3!1!))+(9!/(1!2!6!0!)) + (9!/(1!2!5!1!)) + (9!/(1!2!4!2!))+
+(9!/(0!1!8!0!)) + (9!/(0!1!7!1!) + (9!/(0!1!6!2!) + (9!/(0!1!5!3!)))=
=38521/131072

effettivamente 29.18% ,quello che non capisco è la discrepanza di un'unità fra i 2 numeratori :

76501/262144 (il tuo) 76502/262144 (il mio)

[panurgo]

Un pedone può muoversi su una scacchiera infinita a destra, a sinistra, avanti e indietro di una casella alla volta



Assegnamo uguali probabilità a ciascuna mossa indipendentemente dalla mossa che la precede.

$p\left(X\/\middle|\/Y\/I\right)\/=\/p\left(X\/\middle|\/I\right)\/=\/\frac14$

Una considerazione: il pedone si muove su una griglia di posizioni con diversa parità; se fa un numero pari di mosse arriva in una casa di colore uguale a quello di partenza altrimenti arriva in una casa dell'altro colore.
Consideriamo dunque il caso di $2n$ mosse. Di queste $i$ sono a destra, $j$ a sinistra, $k$ avanti e il resto indietro: poiché la probabilità di ciascuna mossa è indipendente dalla mossa che precede la probabilità di ciascun gruppo di $2n$ mosse è la stessa indipendentemente dall'ordine con cui le mosse vengono eseguite (così come indipendente dall'ordine è la casella di arrivo)

$p\left(i\/j\/k\/\middle|\/2n\/I\right)\/=\frac{\left(2n\right)!} {i!\/j!\/k!\/\left(2n-i-j-k\right)!}\/\left(\frac14\right)^{\script 2n}$


$\left(1/4\right)^{\script 2n}$ è la probabilità di una qualunque sequenza di $2n$ mosse mentre il coefficiente multinomiale enumera tutte le sequenze con la composizione $\left(i,j,k,2n\right)$.
Se le probabilità delle diverse mosse fossero sempre indipendenti dalla mossa che precede ma diverse una dall'altra avremmo

$p\left(i\/j\/k\/\middle|\/2n\/I\right)\/=\frac{\left(2n\right)!} {i!\/j!\/k!\/\left(2n-i-j-k\right)!}\/p^{\script i}\/q^{\script j}\/r^{\script k}\/\left(1\/-\/p\/-\/q\/-\/r\right)^{\script 2n-i-j-k}$

Qual è dunque la probabilità di tornare nella casa di partenza ($H$)? Si torna a casa se e solo se si fanno tanti passi a destra quanti a sinistra e tanti avanti quanti indietro cioè

$p\left(H\/\middle|\/2n\/I\right)\/=\/\frac1{4^{\script 2n}}\/\sum_{\script i\/=\/0}^{\script n}{\frac{\left(2n\right)!}{i!\/i!\/\left(n-i\right)!\/\left(n-i\right)!}}\/=\/\frac{\Gamma\left(n\/+\/1/2\right)^{\script 2}}{\pi\/\Gamma\left(n\/+\/1\right)^{\script 2}}$

La sommatoria ha una graziosa forma chiusa (chiedetelo a Mathematica) e ponendo $2n\/=\/ 10$ riotteniamo il valore già postato

$p\left(H\/\middle|\/10\/I\right)\/=\/\frac{3969}{65536}$

Non è particolarmente difficile neppure la terza domanda: se consideriamo il braccio verticale della croce



possiamo osservare che corrisponde alle mosse possibili quando il numero di passi a destra equaglia quello dei passi a sinistra mentre i restanti passi possono essere suddivisi liberamente tra avanti e indietro

$p\left(B\/\middle|\/2n\/I\right)\/=\/\frac1{4^{\script 2n}}\/\sum_{\script i\/=\/0}^{\script n}{\sum_{\script k\/=\/0}^{\script 2n\/-\/2i}{\frac{\left(2n\right)!} {i!\/i!\/k!\/\left(2n-2i-k\right)!}}}$

Naturalmente, la probabilità di cadere nell'altro braccio è uguale



e la probabilità di cadere nella croce



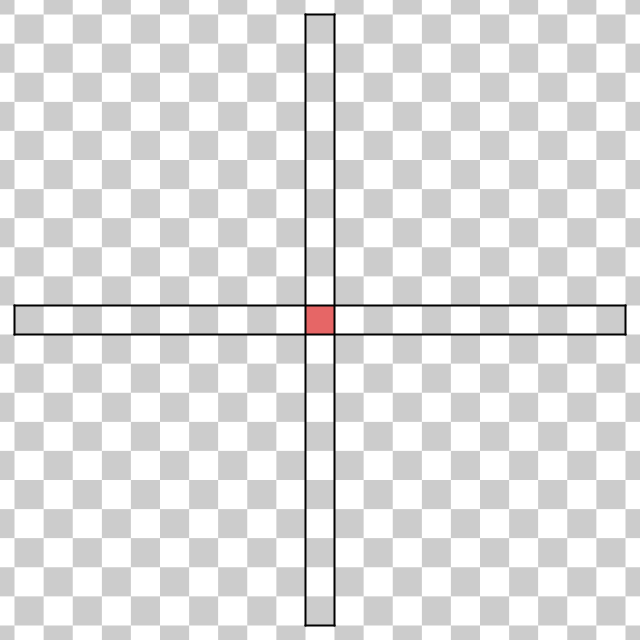
vale

$p\left(C\/\middle|\/2n\/I\right)\/=\/2p\left(B\/\middle|\/2n\/I\right)\/-\/p\left(H\/\middle|\/2n\/I\right)$

cioè due volte la probabilità di un braccio meno la probabilità della casella in comune (la "casa" del primo caso).
Mathematica ci fa il favore di sommare il tutto

$p\left(C\/\middle|\/10\/I\right)\/=\/\frac{38251}{131072}$

Il secondo caso è un po' più macchinoso



La condizione per cadere nel quadrato $5\/\times\/5$ è che sia la differenza tra destra e sinistra sia quella tra avanti e indietro non superi $2$

$\left\{\begin{array}{l}\left|i\/-\/j\right|\/\leq\/2 \\ \left|k\/-\/\left(2n\/-\/i\/-\/j\/-\/k\right)\right|\/\leq\/2 \\ \end{array}\right.$

Poniamo (senza perdita di generalità perchè basta scambiare la destra con la sinistra) $i\/\geq\/j$: dato che $i\/+\/j\/\leq\/2n$ allora

$\left\{\begin{array}{l}i\/+\/j\/\leq\/2n \\ i\/-\/j\/\leq\/2 \\ \end{array}\right.$

Sommiamo le due diseguaglianze scoprendo che $0\/\leq\/i\/\leq\/n\/+\/1$.
Fissato $i$, abbiamo che

$\max\left(0,i\/-\/2\right)\/\leq\/j\/\leq\/\min\left(n\/+\/1,i\/+\/2\right)$

cioè $j$ varia tra $i\/-\/2$ e $i\/+\/2$ se compresi tra $0$ e $n\/+\/1$.
Fissati $i$ e $j$ le cose si complicano: il numero di mosse rimaste a disposizione può essere sia pari sia dispari. Se è

$2n\/-\/i\/-\/j\/=\/2m$

allora i valori possibili di $k$ vanno da $m\/-\/1$ a $m\/+\/1$ mentre se è

$2n\/-\/i\/-\/j\/=\/2m\/+\/1$

i valori possibili di $k$ vanno da $m$ a $m\/+\/1$: sinteticamente

$\max\left(0,\lceil\frac{2n-i-j}2\rceil\/-\/1\right)\/\leq\/k\/\leq\/\min\left(2n\/-\/i\/-\/j,\lfloor\frac{2n-i-j}2\rfloor\/+\/1\right)$

dove $\lceil x\rceil$ e $\lfloor x\rfloor$ sono rispettivamente il più piccolo intero maggiore e il più grande intero minore di $x$.

La probabilità cercata è dunque

$\left\{\begin{array}{l} p\left(Q\/\middle|\/2n\/I\right)\/=\/\frac1{4^{\script 2n}}\/\sum_{\script i}{\sum_{\script i}{\sum_{\script k}{\frac{\left(2n\right)!} {i!\/j!\/k!\/\left(2n-i-j-k\right)!}}}} \\ 0\/\leq\/i\/\leq\/n\/+\/1 \\ \max\left(0,i\/-\/2\right)\/\leq\/j\/\leq\/\min\left(n\/+\/1,i\/+\/2\right) \\ \max\left(0,\lceil\frac{2n-i-j}2\rceil\/-\/1\right)\/\leq\/k\/\leq\/\min\left(2n\/-\/i\/-\/j,\lfloor\frac{2n-i-j}2\rfloor\/+\/1\right) \\ \end{array} \right.$

Lasciamo ancora a Mathematica l'ingrato compito di sommare (oppure usiamo un foglio di Excel) e otteniamo

$p\left(Q\/\middle|\/10\/I\right)\/=\/\frac{4473}{8192}$

Baci