Un volo fra i tulipani

[David]

In un prato si contano 109 tulipani gialli e 81 tulipani rossi.
Due differenti gruppi di api si dirigono verso di essi,il primo drappello farà raccolta solo sui gialli, il secondo si poserà solo sui rossi.
Ogni ape del primo gruppo visiterà ciascun tulipano giallo una e una sola volta,ogni ape del secondo gruppo visiterà ciascun tulipano rosso una e una sola volta.
Le poche informazioni certe riguardo questa faccenda sono che:

a) Le visite su ogni tulipano giallo non saranno superiori a 70.

b) Le visite su ogni tulipano rosso non saranno inferiori a 10.

c) Ciascun tulipano giallo avrà più visite di ciascun tulipano rosso.

d) Le visite totali (la somma delle visite di tutti i fiori) sono in numero che compatibilmente coi dati sopra esposti può essere qualsiasi, con l'unica certezza che esse saranno inferiori a 10000.

Alla luce dei dati comunicati stimare l'evento che ogni tulipano giallo riceva più del doppio di visite di quelle ricevute da ogni tulipano rosso

[franco]

Se non ho capito male il problema, così ad occhio direi circa il 13,79%
(salvo errori e considerando che anche un'ape da sola possa fare "gruppo"!)


ciao

[David]

Non ci può essere un gruppo di un'ape poichè come minimo ogni tulipano rosso deve ricevere 10 visite e se ogni ape visita un tulipano una e una sola volta allora il numero minimo delle api del secondo gruppo sarà 10.

Ciao

[franco]

Ma il primo gruppo, che visita i tulipani gialli, potrebbe essere composto da una sola ape, il testo pone un limite superiore (70) ma non un limite inferiore.

Per come ho interpretato il problema, le api "gialle" sono in numero G compreso fra 1 e 70 mentre le api "rosse" sono un numero R compreso fra 10 e 122 (122*81+1*109=9991 ... 123*81+1*109=10072).

Dalle 70*113 possibili combinazioni di G ed R bisogna escludere quelle che generano un numero V di visite totali maggiore o uguale a 10000 (V=109G+81R) e poi vedere in quale percentuale delle combinazioni restanti è verificata la condizione G>2R

ciao

[David]

Franco hai tralasciato il punto c) che ci informa che ciascun tulipano giallo avrà più visite di ciascun tulipano rosso perciò il numero minimo del primo gruppo è 11 api.
A parte questo dettaglio ininfluente ai fini del ragionamento il metodo risolutivo è corretto.
Bye

[franco]

Hai ragione, la condizione c) mi era completamente sfuggita

Nel nuovo contesto, direi che siamo allora sul 43,62% (sempre a naso e salvo ulteriori svarioni).

ciao

[David]

Darò una rivisitatina ai miei calcoli,sono un pò sopra al 46%,probabilmente ho commesso qualche errore.

Ciao

[franco]

Io non ho fatto calcoli ma solo preparato un programmino in basic che li facesse per me.

Questo è il listato, che non escludo essere sbagliato

LET tot=0
LET fav=0
FOR r=10 TO 69
FOR g=r+1 TO 70
LET v=109*g+81*r
IF v<10000 THEN
LET tot=tot+1
IF g>2*r THEN
LET fav=fav+1
END IF
END IF
NEXT g
NEXT r
PRINT fav
PRINT tot
PRINT fav/tot*100;"%"
END


ciao

[delfo52]

ho il sospetto che le cose cambino, a seconda dell'insieme dei dati di partenza, che si estrapolano dal testo.
Se interpreto bene la stringa di programma di Franco, egli prende in considerazione un numero di api "rosse" tra 10 e 70.
ma, se ho fatto bene i conti, esse non possono essere più di 52, altrimenti il numero totali di visite eccede diecimila.
nel caso r=52, per forza g=53 e non è il doppio

Mi sembra di capire che l'universo delle situazione da considerare è solo quello con r compreso tra 10 e 52
queste 43 "situazioni" dobbiamo considerarle equiprobabili?
e per ognuna di esse il numero di api gialle è equamente distribuito tra r+1 e il massimo compatibile col limite di 10.000 ?
o dobbiamo contare come "1" ogni possibile combinazione di due numeri (r , g) compatibile?
Le cose cambiano, eccome !
se divido prima il "campo delle possibilità" in 43 eventi equiprobabili, la rara situazione (r=52; g=53) avrà lo stesso peso delle numerose coppie che prendono avvio da (g=10), tra cui molte "buone"

[franco]

Nel programma ho fatto lavorare il PC sino ad un massimo di 70 api "rosse", pur sapendo che ciò avrebbe generato un numero v di voli superiori a 10000.
Ciò però non cambia il risultato, infatti la variabile tot si incrementa solo se v<10000. (1)
I casi favorevoli sono rappresentati con la variabile fav che si incrementa quando v<10000 e g>2r.
Tutte le combinazioni di api rosse e gialle sono considerate equiprobabili e quindi il risultato finale è dato dal rapporto fav/tot.

Al di la però del diletto nello scrivere un programmino in basic (cosa che avevo smesso di fare qualche decina di anni fa) sarebbe interessante uno sviluppo più classico del problema.

Purtroppo però il problema mi sembra troppo tosto per i miei denti!

ciao

(1) si può verificare ciò aumentando a piacere il limite superiore; il risultato finale resta sempre pari al 43,62...%

[panurgo]

Dalle condizioni del problema si ricava che il numero di visite per ciascun tulipano, giallo o rosso, è uguale al numero delle api di ciascun gruppo (che chiamerò "api gialle" e "api rosse").
Rappresentando in un piano cartesiano, in ascissa il numero di api gialle e in ordinata quello di api rosse, vediamo che le coppie di valori possibili sono limitate dalle quattro rette

$\begin{array}{lC+25} r_{\script\text 1}\/\equiv\/x\/-\/y\/=\/1 \\ r_{\script\text 2}\/\equiv\/y\/=\/10 \\ r_{\script\text 3}\/\equiv\/x\/=\/70 \\ r_{\script\text 4}\/\equiv\/109x\/+\/81y\/=\/9999 \end{array}$

Le intersezioni di tali rette determinano i vertici di un quadrilatero

$\begin{array}{l+150C} {\text A}\/\equiv\/\left(11,10\right) & {\text B}\/\equiv\/\left(70,10\right) & {\text C}\/\equiv\/\left(70,\frac{2369}{81}\right) & {\text D}\/\equiv\/\left(\frac{1008}{19},\frac{989}{19}\right) \end{array}$

I casi favorevoli sono rappresentati dai punti appartenenti al quadrilatero e inferiori alla retta

$\begin{array}{lC+25} r_{\script\text 5}\/\equiv\/x\/-\/2y\/=\/0 \end{array}$

con intersezioni nei punti

$\begin{array}{l+150C} {\text E}\/\equiv\/\left(20,10\right) & {\text F}\/\equiv\/\left(\frac{19998}{299},\frac{9999}{299}\right) \end{array}$

Ecco il diagramma



Per valori come questi non è troppo disagevole contare i punti, per esempio per mezzo di una tabella come questa

$\begin{array}{c+75C20C+15} x & y_{\script\text \max} & {y \/ < \/ x/2} & {y \/ = \/ x/2} & {y \/ > \/ x/2} & {\text tot.} \\ \hline \\ 11 & 10 & 0 & 0 & 1 & 1 \\ 12 & 11 & 0 & 0 & 2 & 2 \\ 13 & 12 & 0 & 0 & 3 & 3 \\ 14 & 13 & 0 & 0 & 4 & 4 \\ 15 & 14 & 0 & 0 & 5 & 5 \\ 16 & 15 & 0 & 0 & 6 & 6 \\ 17 & 16 & 0 & 0 & 7 & 7 \\ 18 & 17 & 0 & 0 & 8 & 8 \\ 19 & 18 & 0 & 0 & 9 & 9 \\ 20 & 19 & 0 & 1 & 9 & 10 \\ 21 & 20 & 1 & 0 & 10 & 11 \\ 22 & 21 & 1 & 1 & 10 & 12 \\ 23 & 22 & 2 & 0 & 11 & 13 \\ 24 & 23 & 2 & 1 & 11 & 14 \\ 25 & 24 & 3 & 0 & 12 & 15 \\ 26 & 25 & 3 & 1 & 12 & 16 \\ 27 & 26 & 4 & 0 & 13 & 17 \\ 28 & 27 & 4 & 1 & 13 & 18 \\ 29 & 28 & 5 & 0 & 14 & 19 \\ 30 & 29 & 5 & 1 & 14 & 20 \\ 31 & 30 & 6 & 0 & 15 & 21 \\ 32 & 31 & 6 & 1 & 15 & 22 \\ 33 & 32 & 7 & 0 & 16 & 23 \\ 34 & 33 & 7 & 1 & 16 & 24 \\ 35 & 34 & 8 & 0 & 17 & 25 \\ 36 & 35 & 8 & 1 & 17 & 26 \\ 37 & 36 & 9 & 0 & 18 & 27 \\ 38 & 37 & 9 & 1 & 18 & 28 \\ 39 & 38 & 10 & 0 & 19 & 29 \\ 40 & 39 & 10 & 1 & 19 & 30 \end{array}$
$\begin{array}{c+75C+15} 41 & 40 & 11 & 0 & 20 & 31 \\ 42 & 41 & 11 & 1 & 20 & 32 \\ 43 & 42 & 12 & 0 & 21 & 33 \\ 44 & 43 & 12 & 1 & 21 & 34 \\ 45 & 44 & 13 & 0 & 22 & 35 \\ 46 & 45 & 13 & 1 & 22 & 36 \\ 47 & 46 & 14 & 0 & 23 & 37 \\ 48 & 47 & 14 & 1 & 23 & 38 \\ 49 & 48 & 15 & 0 & 24 & 39 \\ 50 & 49 & 15 & 1 & 24 & 40 \\ 51 & 50 & 16 & 0 & 25 & 41 \\ 52 & 51 & 16 & 1 & 25 & 42 \\ 53 & 52 & 17 & 0 & 26 & 43 \\ 54 & 50 & 17 & 1 & 23 & 41 \\ 55 & 49 & 18 & 0 & 22 & 40 \\ 56 & 48 & 18 & 1 & 20 & 39 \\ 57 & 46 & 19 & 0 & 18 & 37 \\ 58 & 45 & 19 & 1 & 16 & 36 \\ 59 & 44 & 20 & 0 & 15 & 35 \\ 60 & 42 & 20 & 1 & 12 & 33 \\ 61 & 41 & 21 & 0 & 11 & 32 \\ 62 & 40 & 21 & 1 & 9 & 31 \\ 63 & 38 & 22 & 0 & 7 & 29 \\ 64 & 37 & 22 & 1 & 5 & 28 \\ 65 & 35 & 23 & 0 & 3 & 26 \\ 66 & 34 & 23 & 1 & 1 & 25 \\ 67 & 33 & 24 & 0 & 0 & 24 \\ 68 & 31 & 22 & 0 & 0 & 22 \\ 69 & 30 & 21 & 0 & 0 & 21 \\ 70 & 29 & 20 & 0 & 0 & 20 \\ \hline \\ & & 639 & 24 & 802 & 1465 \end{array}$

Voglio, invece, utilizzare un metodo alternativo, basato (ma guarda un po') sul teorema di Pick.

L'enunciato del teorema è riferito ad un poligono qualsiasi costruito congiungedo i punti di un reticolo:

$Area\/ = \/I\/ +\/ P/2\/ -\/ 1$

dove $I$ è il numero di punti interni e $P$ è il numero di punti sul perimetro.
Il poligono ${\text ABCD}$ non è un poligono di Pick perché il lato ${\text CD}$ non passa per i punti del reticolo; ciononostante è possibile usare la formula di Pick per ottenere una risposta approssimata calcolando l'area del poligono e contando i soli punti sul perimetro: il numero di punti interni si ottiene mediante la

$I\/=\/Area\/+\/1\/-\/P/2$

e il numero totale di punti è

$N\/=\/I\/+\/P\/=\/Area\/+\/1\/+\/P/2$

Per calcolare l'area del quadrilatero generico ${\text ABCD}$, di cui sono note le coordinate dei vertici, è sufficiente osservare che le congiungenti perpendicolari dei vertici ${\text B}$ e ${\text D}$ alla diagonale ${\text AC}$ sono le altezze rispettivamente dei due triangoli ${\text ABC}$ e ${\text ACD}$ e che

${\text ABCD}\/=\/{\text ABC}\/+\/{\text ACD}$

Purtroppo, non mi ricordo mai la formula per la distanza di un punto da una retta per cui mi serve qualcosa di diverso.
Rappresento i vertici del quadrilatero come vettori

$\begin{array}{l+150C} A\/=\/{ x_{\script\text A} \choose y_{\script\text A}} & B\/=\/{ x_{\script\text B} \choose y_{\script\text B}} & C\/=\/{ x_{\script\text C} \choose y_{\script\text C}} & D\/=\/{ x_{\script\text D} \choose y_{\script\text D}} \end{array}$

Li traslo in modo da portare il vertice più a sinistra, $A$, nell'origine

$\begin{array}{l+150C} A^{\script\prime}\/=\/A\/-\/A & B^{\script\prime}\/=\/B\/-\/A & C^{\script\prime}\/=\/C\/-\/A & D^{\script\prime}\/=\/D\/-\/A \end{array}$

e li ruoto in modo da rendere $C$ orizzontale (vedi figura seguente)



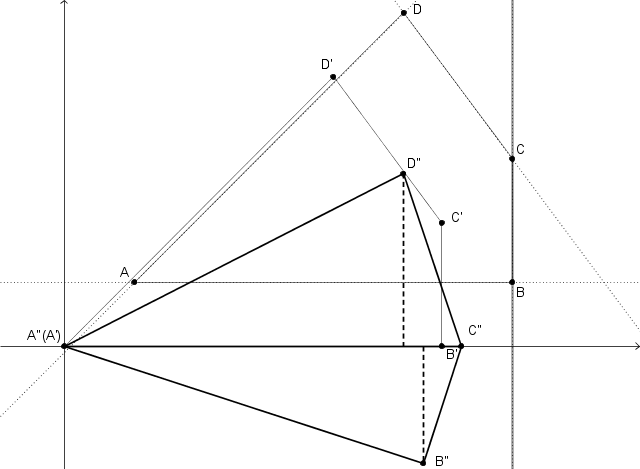
L'operatore per la rotazione di un angolo orientato $\vartheta$ è

$R\/=\/\left(\begin{array}{ccCC} \cos\vartheta & -\/\sin\vartheta \\ \sin\vartheta & \cos\vartheta \end{array}\right)$

per una rotazione in senso orario l'angolo è negativo quindi

$R\/=\/\left(\begin{array}{ccCC} \cos\left|\vartheta\right| & \sin\left|\vartheta\right| \\ -\/\sin\left|\vartheta\right| & \cos\left|\vartheta\right| \end{array}\right)$

Posto $r\/=\/\sqrt{x_{\script\text C}^{\script\prime 2}\/+\/y_{\script\text C}^{\script\prime 2}}$ abbiamo

$\begin{array}{l+120C} \sin\left|\vartheta\right|\/=\/\frac{y_{\script\text C}^{\script\prime}}r & \cos\left|\vartheta\right|\/=\/\frac{x_{\script\text C}^{\script\prime}|}r \end{array}$

cioè

$R\/=\/\frac1r\/\left(\begin{array}{ccCC} x_{\script\text C}^{\script\prime} & y_{\script\text C}^{\script\prime} \\ -\/y_{\script\text C}^{\script\prime} & x_{\script\text C}^{\script\prime} \end{array}\right)$

Una volta operata la rotazione abbiamo

${\text ABCD}\/=\/\frac{x_{\script\text C}^{\script\prime\prime}\/\left(y_{\script\text D}^{\script\prime\prime}\/-\/y_{\script\text B}^{\script\prime\prime}\right)} 2$

ma

$x_{\script\text C}^{\script\prime\prime}\/=\/r$

e

$\begin{array}{lC+60} y_{\script\text B}^{\script\prime\prime}\/=\/\frac1r\/\left(\begin{array}{c+30C} -\/y_{\script\text C}^{\script\prime} & x_{\script\text C}^{\script\prime} \end{array}\right)\/\left(\begin{array}{cC+30} x_{\script\text B}^{\script\prime} \\ y_{\script\text B}^{\script\prime} \end{array}\right)\/=\/\frac{ x_{\script\text C}^{\script\prime} y_{\script\text B}^{\script\prime}\/-\/x_{\script\text B}^{\script\prime} y_{\script\text C}^{\script\prime}}r \\ y_{\script\text D}^{\script\prime\prime}\/=\/\frac1r\/\left(\begin{array}{c+30C} -\/y_{\script\text C}^{\script\prime} & x_{\script\text C}^{\script\prime} \end{array}\right)\/\left(\begin{array}{cC+30} x_{\script\text D}^{\script\prime} \\ y_{\script\text D}^{\script\prime} \end{array}\right)\/=\/\frac{ x_{\script\text C}^{\script\prime} y_{\script\text D}^{\script\prime}\/-\/x_{\script\text D}^{\script\prime} y_{\script\text C}^{\script\prime}}r \end{array}$

quindi

${\text ABCD}\/=\/\frac{x_{\script\text C}^{\script\prime}y_{\script\text D}^{\script\prime}\/-\/x_{\script\text D}^{\script\prime}y_{\script\text C}^{\script\prime}\/-\/x_{\script\text C}^{\script\prime}y_{\script\text B}^{\script\prime}\/+\/x_{\script\text B}^{\script\prime}y_{\script\text C}^{\script\prime}}2\/=\/\frac{x_{\script\text C}^{\script\prime}\/\left(y_{\script\text D}^{\script\prime}\/-\/y_{\script\text B}^{\script\prime}\right)\/-\/\left(x_{\script\text D}^{\script\prime}\/-\/x_{\script\text B}^{\script\prime}\right)\/y_{\script\text C}^{\script\prime}}2$

Ora, essendo

$\begin{array}{lC+35} x_{\script\text C}^{\script\prime}\/=\/x_{\script\text C}\/-\/x_{\script\text A} \\ y_{\script\text C}^{\script\prime}\/=\/y_{\script\text C}\/-\/y_{\script\text A} \\ x_{\script\text D}^{\script\prime }\/-\/x_{\script\text B}^{\script\prime }\/=\/x_{\script\text D}\/-\/x_{\script\text B} \\ y_{\script\text D}^{\script\prime }\/-\/y_{\script\text B}^{\script\prime }\/=\/y_{\script\text D}\/-\/y_{\script\text B} \end{array}$

ne consegue che

${\text ABCD}\/=\/\frac{\left(x_{\script\text C}\/-\/x_{\script\text A}\right)\/\left(y_{\script\text D}\/-\/y_{\script\text B}\right)\/-\/\left(x_{\script\text D}\/-\/x_{\script\text B}\right)\/\left(y_{\script\text C}\/-\/y_{\script\text A}\right)}2$

Questa formula è valida per qualunque quadrilatero convesso o concavo: io l'ho ricavata considerando ${\text A}$ il punto più a destra, ma l'unica condizione necessaria e che i vertici ${\text A}$, ${\text B}$, ${\text C}$ e ${\text D}$ siano ordinati in senso trigonometrico.

Torniamo al nostro problema: l'area di un poligono di Pick è sempre un multiplo della metà dell'area della cella del reticolo e, dato che il nostro reticolo è un reticolo a coordinate intere, le nostre aree saranno multipli di $1/2$.
La formula per l'area del quadrilatero arrotondata all'$1/2$ inferiore è

${\text ABCD}\/=\/\frac{\left\lfloor\left(x_{\script\text C}\/-\/x_{\script\text A}\right)\/\left(y_{\script\text D}\/-\/y_{\script\text B}\right)\/-\/\left(x_{\script\text D}\/-\/x_{\script\text B}\right)\/\left(y_{\script\text C}\/-\/y_{\script\text A}\right)\right\rfloor}2$

dove $\left \lfloor x \right \rfloor$ rappresenta l'intero immediatamente inferiore a $x$.
Abbiamo tre quadrilateri: ABCD, che contiene tutti i casi, AEFD, che contiene i casi con e EBCF, che contiene i casi con . Le rispettive aree valgono

$\begin{array}{lC+45} {\text ABCD}\/=\/\frac{\left\lfloor\left(70\/-\/11\right)\/\left(\frac{989}{19}\/-\/10\right)\/-\/\left(\frac{1008}{19}\/-\/70\right)\/\left(\frac{2369}{81}\/-\/10\right)\right\rfloor}2\/=\/\frac{2807}2 \\ {\text AEFD}\/=\/\frac{\left\lfloor\left(\frac{19998}{299}\/-\/11\right)\/\left({989}{19}\/-\/10\right)\/-\/\left(\frac{1008}{19}\/-\/20\right)\/\left(\frac{9999}{299}\/-\/10\right)\right\rfloor}2\/=\/\frac{1575}2 \end{array}$

e

$\begin{array}{lC+45} {\text EBCF}\/=\/\frac{\left\lfloor\left(70\/-\/20\right)\/\left(\frac{9999}{299}\/-\/10\right)\/-\/\left(\frac{19998}{299}\/-\/70\right)\/\left(\frac{2369}{81}\/-\/10\right)\right\rfloor}2\/=\/\frac{1232}2 \end{array}$

Il numero di punti che giacciono su ciascun segmento è

$\begin{array}{lC+35} {\overset{\LARGE...}{\text AB}}\/=\/x_{\script\text B}\/-\/x_{\script\text A}\/+\/1\/=\/60 \\ {\overset{\LARGE...}{\text BC}}\/=\/\left\lfloor y_{\script\text C}\right\rfloor\/-\/y_{\script\text B}\/+\/1\/=\/20 \\ {\overset{\LARGE...}{\text CD}}\/=\/0 \\ {\overset{\LARGE...}{\text AD}}\/=\/\left\lfloor x_{\script\text D}\right\rfloor\/-\/x_{\script\text A}\/+\/1\/=\/43 \\ {\overset{\LARGE...}{\text AE}}\/=\/x_{\script\text E}\/-\/x_{\script\text A}\/+\/1\/=\/11 \\ {\overset{\LARGE...}{\text EF}}\/=\/\left\lfloor y_{\script\text F}\right\rfloor\/-\/y_{\script\text E}\/+\/1\/=\/24 \\ {\overset{\LARGE...}{\text DF}}\/=\/0 \\ {\overset{\LARGE...}{\text BE}}\/=\/x_{\script\text B}\/-\/x_{\script\text E}\/+\/1\/=\/51 \\ {\overset{\LARGE...}{\text CF}}\/=\/0} \end{array}$

Alla lunghezza di ciascun segmento viene sempre aggiunto un punto perche $n$ segmenti unitari sono delimitati da $n\/ +\/ 1$ punti; i segmenti che appartengono alla retta $r_{\script\text 4}$ non contengono punti.
Ciò detto, i "perimetri" dei tre quadrilateri contengono rispettivamente $121$, $75$ e $93$ punti

$\begin{array}{lC+35} 2p_{\script\text ABCD}\/=\/{\overset{\LARGE...}{\text AB}}\/+\/{\overset{\LARGE...}{\text BC}}\/+\/{\overset{\LARGE...}{\text CD}}\/+\/{\overset{\LARGE...}{\text AD}}\/-\/2\/=\/121 \\ 2p_{\script\text AEFD}\/=\/{\overset{\LARGE...}{\text AE}}\/+\/{\overset{\LARGE...}{\text EF}}\/+\/{\overset{\LARGE...}{\text CF}}\/+\/{\overset{\LARGE...}{\text AD}}\/-\/2\/=\/75 \\ 2p_{\script\text EBCF}\/=\/{\overset{\LARGE...}{\text EB}}\/+\/{\overset{\LARGE...}{\text BC}}\/+\/{\overset{\LARGE...}{\text CF}}\/+\/{\overset{\LARGE...}{\text EF}}\/-\/2\/=\/93 \end{array}$

Alla somma dei quattro "lati" vengono sottratti tanti punti quanti sono quelli in comune alle coppie di segmenti successivi: i segmenti contenenti $0$ punti non hanno punti in comune con i segmenti adiacenti.
Possiamo ora contare il numero totale dei punti nei tre quadrilateri

$\begin{array}{lC+35} n_{\script\text ABCD}\/=\/{\text ABCD}\/+\/1\/+\/p_{\script\text ABCD}\/=\/\frac{1807}2\/+\/1\/+\/\frac{121}2\/=\/1465 \\ n_{\script\text AEFD}\/=\/{\text AEFD}\/+\/1\/+\/p_{\script\text AEFD}\/=\/\frac{1575}2\/+\/1\/+\/\frac{75}2\/=\/826 \\ n_{\script\text EBCF}\/=\/{\text EBCF}\/+\/1\/+\/p_{\script\text EBCF}\/=\/616\/+\/1\/+\/\frac{93}2\/=\/663\/+\/\frac12 \end{array}$

Abbastanza ovviamente bisogna considerare solo un numero intero di punti e, dato che l'area del quadrilatero può essere solo troppo grande, approssimo all'intero inferiore: $n_{\script\text EBCF}\/ =\/ 663$.
I quadrilateri ${\text AEFD}$ e ${\text EBCF}$ contengono rispettivamente i punti per i quali $y\/\geq\/x/2$ e $y\/\leq\/x/2$, quindi a ciascuno dei due bisogna togliere i $24$ punti per i quali $y\/=\/x/2$ ottenendo

$\begin{array}{c+75C20C+15} {y \/ < \/ x/2} & {y \/ = \/ x/2} & {y \/ > \/ x/2} & {\text tot.} \\ \hline \\ 639 & 24 & 802 & 1465 \end{array}$

il che mi sembra un'approssimazione difficilmente migliorabile.