Permutazioni regolari

[giobimbo]

Sia P una permutazioni dei numeri da 1 a 9, per esempio
P = 6 2 5 8 4 1 9 3 7.

Ad ogni elemento di P aggiungiamo uno, sommando modulo 9, otteniamo
P1 = 7 3 6 9 5 2 1 4 8.

Ad ogni elemento di P1 aggiungiamo uno, sommando modulo 9, otteniamo
P2 = 8 4 7 1 6 3 2 5 9.

Si continua così fino ad arrivare a P8, poi mettendo le nove permutazioni una sopra l'altra si dovrebbe avere la sottostante tabella 9x9:

6 2 5 8 4 1 9 3 7
7 3 6 9 5 2 1 4 8
8 4 7 1 6 3 2 5 9
9 5 8 2 7 4 3 6 1
1 6 9 3 8 5 4 7 2
2 7 1 4 9 6 5 8 3
3 8 2 5 1 7 6 9 4
4 9 3 6 2 8 7 1 5
5 1 4 7 3 9 8 2 6

Scambiamo tra loro le righe in modo da avere la diagonale principale composta da tutti 9, coloriamo di rosso l'elemento 1 della prima colonna, l'elemento 2 della seconda colonna, ..., l'elemento 9 dell'ultima colonna; avremo una tabella come questa sotto:

9 5 8 2 7 4 3 6 1
4 9 3 6 2 8 7 1 5
1 6 9 3 8 5 4 7 2
7 3 6 9 5 2 1 4 8
2 7 1 4 9 6 5 8 3
5 1 4 7 3 9 8 2 6
6 2 5 8 4 1 9 3 7
3 8 2 5 1 7 6 9 4
8 4 7 1 6 3 2 5 9

I numeri da 1 a 5 stanno tutti in righe diverse, mentre 6 è nella stessa riga di 4; diremo allora che P=6 2 5 8 4 1 9 3 7 è regolare di grado 5 (primi 5 numeri in 5 righe diverse).

Trovare una permutazione dei numeri da 1 a 9 che sia regolare di grado n>5 (primi n numeri in n righe diverse).

[franco]

Aspetta un attimo, non mi torna il conto.

I numeri 1 e 2 sono in righe diverse ma il 3 è nella stessa riga del 7 ed il 4 è nella stessa riga di 6 ed 8.

La tua permutazione di partenza non dovrebbe quindi essere considerata di grado 2?

ciao

[franco]

Probabilmente ho capito male perchè mi viene una soluzione banale per ottenere addiritura un grado 9:


Peraltro, dal tuo esempio, non capisco che "valore aggiunto" abbia l'ordinare le righe per avere il 9 nella colonna principale (i numeri rossi che erano da soli in una riga lo restano anche dopo aver mischiato le righe stesse).

Aumenta il dubbio che io non abbia capito nulla!

ciao

[giobimbo]

Un paio di anni fa avevo proposto un problema, "Pedine in ordine sparso", affine a questo e qualcuno - non faccio nomi - aveva subito trovato una soluzione banale. Memore di ciò ho controllato se per caso
P = 1 2 3 4 5 6 7 8 9
non fosse una permutazione regolare di grado 9: no, bene, mettiamo il problema sul Forum. Bene un corno, perché la sua opposta è una soluzione del problema. Per colpa della mia disattenzione ho rovinato tutto, bastava che avessi proibito di usarla perché banale, oppure che avessi chiesto di usare permutazioni dei numeri da 1 a 8, o da 1 a 10.

Il grado n della permutazione è dato dai primi n numeri che stanno in n righe diverse, se un numero m è maggiore di n, m>n, ovviamente esso sarà in una riga che ha gia un numero, ma m non contribuisce più a formare il grado.
Per n dispari il massimo grado di P è n, per n pari il massimo grado è n-1.

Peraltro, dal tuo esempio, non capisco che "valore aggiunto" abbia l'ordinare le righe per avere il 9 nella colonna principale

Qui penso che tu intendessi la diagonale principale, nel qual caso ti dico di provare a trovare una permutazione P di grado 9, una P diversa dalle nove che stanno nella tua tabella.

Mi correggo, sostituire ovviamente esso sarà con:
"può ben darsi che esso capiti"
In blu alcune parole aggiunte in seguito.

[franco]

Quello che non capivo era il motivo di scambiare fra loro le righe per formare la diagonale di 9;

la tabella originale dovrebbe avere, se ho capito bene, lo stesso grado di quella ordinata:

6 2 5 8 4 1 9 3 7
7 3 6 9 5 2 1 4 8
8 4 7 1 6 3 2 5 9
9 5 8 2 7 4 3 6 1
1 6 9 3 8 5 4 7 2
2 7 1 4 9 6 5 8 3
3 8 2 5 1 7 6 9 4
4 9 3 6 2 8 7 1 5
5 1 4 7 3 9 8 2 6

9 5 8 2 7 4 3 6 1
4 9 3 6 2 8 7 1 5
1 6 9 3 8 5 4 7 2
7 3 6 9 5 2 1 4 8
2 7 1 4 9 6 5 8 3
5 1 4 7 3 9 8 2 6
6 2 5 8 4 1 9 3 7
3 8 2 5 1 7 6 9 4
8 4 7 1 6 3 2 5 9

(ho usato il colore rosso per indicare i numeri che riesco ad inserire su righe distinte prima di incappare nella prima ripetizione; da lì in aventi li ho messi in blu)

Adesso comunque il problema è chiaro; non ho però idea della strada da percorrere, salvo il fare tentativi a casaccio (come ho fatto ieri) oppure provare tutte le 9! permutazioni possibili (esclusa quella vietata ).

ciao

[panurgo]

Ho affidato ad un volenteroso PC il poco appetibile compito di scandire tutte le $9!\/=\/362880$ permutazioni delle nove cifre. Per ogni permutazione gli ho fatto calcolare il grado e così ho trovato che i vari gradi sono così rappresentati:

$\begin{array}{l|r} {\text grado} & n \\ \hline \\ 1 & 45360 \\ 2 & 77760 \\ 3 & 85320 \\ 4 & 73440 \\ 5 & 47250 \\ 6 & 23256 \\ 7 & 8469 \\ 8 & 0 \\ 9 & 2025 \\ \end{array}$

in grafico



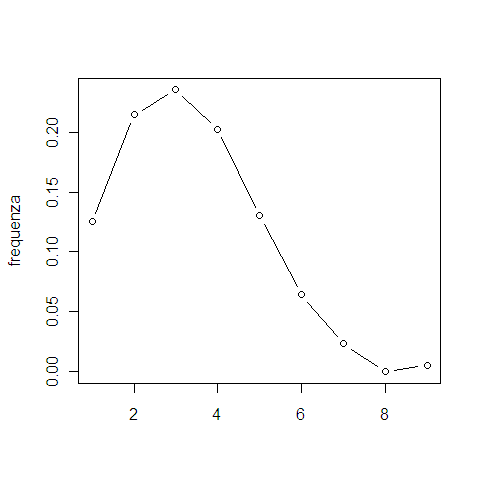
Ciò che mi sembra necessario spiegare è quello $0$ per il grado $8$ (ci sto lavorando).

[giobimbo]

Franco, hai ragione, mettere tutti 9 nella diagonale principale è un lavoro inutile al fine della ricerca del grado, non avevo capito cosa intendevi ma adesso con i numeri colorati mi è tutto più chiaro. In quanto ai tentativi a casaccio direi che questo è proprio il primo passo da fare davanti a un problema da risolvere, quando tale problema non rientra in una classe mai affrontata prima, poi dai dati si cerca di trovare quale logica sta sotto alla loro esistenza. Io essendo più coinvolto nel problema ormai ho come un paraocchi che m'impedisce di vedere bene cosa c'è dalle parti della strada che percorro, per cui spero che qualcun altro faccia delle osservazioni che mi siano utili, come quella dell'esistenza della soluzione banale.

Scusa Panurgo, mi potresti controllare i casi n=6 e n=8 per vedere se anche lì non ci sono permutazioni regolari di grado n-1?

[panurgo]

sto facendo un po' di euristica: posto qualcosa quanto prima

[David]

Per stabilire l'ordine di una permutazione si può eseguire il seguenta procedimento a cascata:

poniamo che le 9 cifre scritte siano abcdefghi allora abbiamo questi eventi mutuamente esclusivi:

ordine 1 se:

b-a=1

ordine 2 se:

c-a=2 o c-b=1

ordine 3:

d-a=3 o d-b=2 o d-c=1

ordine 4:

e-a=4 o e-b=3 o e-c=2 o e-d=1 ecc

Esempio la tua permutazione di partenza 6 2 5 8 4 1 9 3 7 si constata essere di ordine 5 poichè:
b-a=5
c-a=8
c-b=3
d-a=2
d-b=6
d-c=3
e-a=7
e-b=2
e-c=8
e-d=5
nessun valore dei primi 4 ordini combacia coi suddetti mentre :
f-d=2
infatti per il quinto ordine deve verificarsi una delle seguenti uguaglianze:
f-a=5
f-b=4
f-c=3
f-d=2
f-e=1
quindi per scrivere una permutazione di ordine superiore a 5 bisogna porre le cifre in maniera che nessuna delle eguaglianze scritte sia rispettata.
Questo per il momento è quello che posso dire.

[panurgo]

Punto primo, il procedimento di Giobimbo genera, a partire da una permutazione data, le altre $n\/-\/1$ permutazioni che formano con essa un gruppo ciclico: sono cioè permutazioni in cui l'ordine dei simboli è lo stesso solo a partire da un simbolo ogni volta diverso. Ciò significa che è necessario controllare solo le permutazioni che cominciano con un dato simbolo, per esempio l'$1$.
Se $n\/=\/3$ abbiamo (tralascio i casi $1$ e $2$ che sono banali)

$\begin{array}{c160c160} \begin{array}{l|r20C75} {\begin{array}{c25c25c25C25C25C25} \compose{\circle(18)}{1}&\compose{\circle(18)}{2}&\compose{\circle(18)}{3} \\ 2&3&1 \\ 3&1&2 \\ \end{array}} & {\LARGE 1} \\ \end{array} & \begin{array}{l|r20C75} {\begin{array}{c25c25c25C25C25C25} \compose{\circle(18)}{1}&3&2 \\ 2&1&\compose{\circle(18)}{3} \\ 3&\compose{\circle(18)}{2}&1 \\ \end{array}} & {\LARGE 3} \\ \end{array} \\ \end{array}$

Come si vede, sono elencate tutte e sei le permutazioni di tre simboli, tre di grado $1$ e tre di grado $3$: come si vede non ve ne sono di grado $2$.
Se $n\/=\/4$ abbiamo

$\begin{array}{c160c160c160C160R180} \begin{array}{l|r20C100} \begin{array}{c25c25c25c25C25C25C25C25} \compose{\circle(18)}{1}&\compose{\circle(18)}{2}&\compose{\circle(18)}{3}&\compose{\circle(18)}{4} \\ 2&3&4&1 \\ 3&4&1&2 \\ 4&1&2&3 \\ \end{array} & {\LARGE 1} \\ \end{array} & \begin{array}{l|r20C100} \begin{array}{c25c25c25c25C25C25C25C25} \compose{\circle(18)}{1}&\compose{\circle(18)}{2}&4&3 \\ 2&3&1&\compose{\circle(18)}{4} \\ 3&4&2&1 \\ 4&1&\compose{\circle(18)}{3}&2 \\ \end{array} & {\LARGE 1} \\ \end{array} & \begin{array}{l|r20C100} \begin{array}{c25c25c25c25C25C25C25C25} \compose{\circle(18)}{1}&3&2&\compose{\circle(18)}{4} \\ 2&4&\compose{\circle(18)}{3}&1 \\ 3&1&4&2 \\ 4&\compose{\circle(18)}{2}&1&3 \\ \end{array} & {\LARGE 3} \\ \end{array} \\ \begin{array}{l|r20C100} \begin{array}{c25c25c25c25C25C25C25C25} \compose{\circle(18)}{1}&3&4&2 \\ 2&4&1&3 \\ 3&1&2&\compose{\circle(18)}{4} \\ 4&\compose{\circle(18)}{2}&\compose{\circle(18)}{3}&1 \\ \end{array} & {\LARGE 2} \\ \end{array} & \begin{array}{l|r20C100} \begin{array}{c25c25c25c25C25C25C25C25} \compose{\circle(18)}{1}&4&2&3 \\ 2&1&\compose{\circle(18)}{3}&\compose{\circle(18)}{4} \\ 3&\compose{\circle(18)}{2}&4&1 \\ 4&3&1&2 \\ \end{array} & {\LARGE 3} \\ \end{array} & \begin{array}{l|r20C100} \begin{array}{c25c25c25c25C25C25C25C25} \compose{\circle(18)}{1}&4&\compose{\circle(18)}{3}&2 \\ 2&1&4&3 \\ 3&\compose{\circle(18)}{2}&1&\compose{\circle(18)}{4} \\ 4&3&2&1 \\ \end{array} & {\LARGE 2} \\ \end{array} \\ \end{array}$

e vi sono otto permutazioni per ogni grado, $4$ escluso.
Avrete notato che non ho perduto tempo a riordinare le righe: come avete già scritto precedentemente è perfettamente inutile poiché, se due numeri corrispondenti alla colonna in cui si trovano sono sulla stessa riga, lo sono indipendentemente dalla posizione della riga stessa. Due permutazioni che appartengono allo stesso gruppo ciclico portano alla stessa matrice!
Un altro po' di riflessione mi ha portato a capire che, in realtà, non è neppure necessario costruire il gruppo delle permutazioni cicliche: infatti tutte le permutazioni derivano dalla prima secondo una regola precisa e quindi non portano alcuna informazione che non sia già contenuta in quella di partenza e nella regola stessa.
Prendiamo il caso $n\/=\/4$: cominciamo a scrivere

$\begin{array}{c25c25c25c25|c30|r50C25} \compose{\circle(18)}{1}&\compose{\circle(18)}{2} \\ \end{array}$

È evidente che tutte le permutazioni che cominciano così saranno di grado $1$ e sono in tutto $2!\/\times\/4$: $2!$ perché vi sono altri due simboli e $4$ perché considero solo le permutazioni che iniziano per $1$. Continuiamo

$\begin{array}{c25c25c25c25|c30|r50C25} \compose{\circle(18)}{1}&\compose{\circle(18)}{2}&&&1& 2!\/\times\/4 \\ \compose{\circle(18)}{1}&3&2&\compose{\circle(18)}{4}&3& 0!\/\times\/4 \\ \end{array}$

Anche questa volta abbiamo un secondo numero corrispondente alla colonna, il $4$: vi sono $0$ simboli residui per cui abbiamo $0!\/\times\/4$ permutazioni di grado $3$.
Ancora

$\begin{array}{c25c25c25c25|c30|r50C25} \compose{\circle(18)}{1}&\compose{\circle(18)}{2}& & &1& 2!\/\times\/4 \\ \compose{\circle(18)}{1}&3&2&\compose{\circle(18)}{4}&3& 0!\/\times\/4 \\ 1&\compose{\circle(18)}{3}&\compose{\circle(18)}{4}& &2& 1!\/\times\/4 \\ \end{array}$

In questo caso, abbiamo due numeri successivi uno vicino all'altro: in questa permutazione non corrispondono alle colonne in cui si trovano ma la permutazione giusta fa parte comunque del gruppo ciclico. Il $3\/4$ diventa $4\/1$, $1\/2$ ed infine $2\/3$: ecco il bandolo della matassa, in una qualunque permutazione si devono cercare i due numeri la cui differenza sia congruente modulo $n$ alla distanza che li separa.
Ed ecco la tabella completa

$\begin{array}{c25c25c25c25|c30|r50C25} &&&&r&{\text num.} \\ \hline \\ \compose{\circle(18)}{1}&\compose{\circle(18)}{2}& & &1& 2!\/\times\/4 \\ \compose{\circle(18)}{1}&3&2&\compose{\circle(18)}{4}&3& 0!\/\times\/4 \\ 1&\compose{\circle(18)}{3}&\compose{\circle(18)}{4}& &2& 1!\/\times\/4 \\ 1&4&\compose{\circle(18)}{2}&\compose{\circle(18)}{3}&3& 0!\/\times\/4 \\ \compose{\circle(18)}{1}&4&\compose{\circle(18)}{3}& &2& 1!\/\times\/4 \\ \end{array}$

La tabella per $n\/=\/5$

$\begin{array}{c25c25c25c25c25|c30|r50C25} &&&&&r&{\text num.} \\ \hline \\ \compose{\circle(18)}{1}&\compose{\circle(18)}{2}& & & &1&3!\/\times\/5 \\ \compose{\circle(18)}{1}&3&2&\compose{\circle(18)}{4}& &3&1!\/\times\/5 \\ 1&\compose{\circle(18)}{3}&2&\compose{\circle(18)}{5}& &3&1!\/\times\/5 \\ 1&\compose{\circle(18)}{3}&\compose{\circle(18)}{4}& & &2&2!\/\times\/5 \\ 1&3&5&2&4&5&0!\/\times\/5 \\ \compose{\circle(18)}{1}&3&5&\compose{\circle(18)}{4}& &3&1!\/\times\/5 \\ 1&4&\compose{\circle(18)}{2}&\compose{\circle(18)}{3}& &3&1!\/\times\/5 \\ 1&4&2&5&3&5&0!\/\times\/5 \\ \compose{\circle(18)}{1}&4&\compose{\circle(18)}{3}& & &2&2!\/\times\/5 \\ 1&\compose{\circle(18)}{4}&\compose{\circle(18)}{5}& & &2&2!\/\times\/5 \\ 1&5&\compose{\circle(18)}{2}&\compose{\circle(18)}{3}& &3&1!\/\times\/5 \\ \compose{\circle(18)}{1}&5&2&\compose{\circle(18)}{4}& &3&1!\/\times\/5 \\ \compose{\circle(18)}{1}&5&\compose{\circle(18)}{3}& & &2&2!\/\times\/5 \\ 1&\compose{\circle(18)}{5}&4&\compose{\circle(18)}{2}& &3&1!\/\times\/6 \\ 1&5&4&3&2&5&0!\/\times\/5 \\ \end{array}$

La tabella per $n\/=\/6$

$\begin{array}{c25c25c25c25c25c25|c30|r50C25} &&&&&&r&{\text num.} \\ \hline \\ \compose{\circle(18)}{1}&\compose{\circle(18)}{2}&&&&&1&4!\/\times\/6 \\ \compose{\circle(18)}{1}&3&2&\compose{\circle(18)}{4}&&&3&2!\/\times\/6 \\ 1&\compose{\circle(18)}{3}&2&\compose{\circle(18)}{5}&&&3&2!\/\times\/6 \\ 1&3&\compose{\circle(18)}{2}&6&\compose{\circle(18)}{4}&&4&1!\/\times\/6 \\ \compose{\circle(18)}{1}&3&2&6&\compose{\circle(18)}{5}&&4&1!\/\times\/6 \\ 1&\compose{\circle(18)}{3}&\compose{\circle(18)}{4}&&&&2&3!\/\times\/6 \\ \compose{\circle(18)}{1}&3&5&2&4&\compose{\circle(18)}{6}&5&0!\/\times\/6 \\ 1&\compose{\circle(18)}{3}&5&2&\compose{\circle(18)}{6}&&4&1!\/\times\/6 \\ \compose{\circle(18)}{1}&3&5&\compose{\circle(18)}{4}&&&3&2!\/\times\/6 \\ 1&3&\compose{\circle(18)}{5}&\compose{\circle(18)}{6}&&&3&2!\/\times\/6 \\ 1&3&6&2&\compose{\circle(18)}{4}&\compose{\circle(18)}{5}&5&0!\/\times\/6 \\ \compose{\circle(18)}{1}&3&6&\compose{\circle(18)}{4}&&&3&2!\/\times\/6 \\ 1&\compose{\circle(18)}{3}&6&\compose{\circle(18)}{5}&&&3&2!\/\times\/6 \\ 1&4&\compose{\circle(18)}{2}&\compose{\circle(18)}{3}&&&3&2!\/\times\/6 \\ \compose{\circle(18)}{1}&4&2&5&3&\compose{\circle(18)}{6}&5&0!\/\times\/6 \\ 1&4&2&\compose{\circle(18)}{5}&\compose{\circle(18)}{6}&&4&1!\/\times\/6 \\ \end{array}$
$\begin{array}{c25c25c25c25c25c25|c30|r50C25} 1&\compose{\circle(18)}{4}&2&\compose{\circle(18)}{6}&&&4&1!\/\times\/6 \\ \compose{\circle(18)}{1}&4&\compose{\circle(18)}{3}&&&&2&3!\/\times\/6 \\ 1&\compose{\circle(18)}{4}&\compose{\circle(18)}{5}&&&&2&3!\/\times\/6 \\ 1&4&6&\compose{\circle(18)}{2}&\compose{\circle(18)}{3}&&4&1!\/\times\/6 \\ \compose{\circle(18)}{1}&4&6&2&\compose{\circle(18)}{5}&&4&1!\/\times\/6 \\ 1&4&\compose{\circle(18)}{6}&3&\compose{\circle(18)}{2}&&4&1!\/\times\/6 \\ \compose{\circle(18)}{1}&4&6&3&\compose{\circle(18)}{5}&&4&1!\/\times\/6 \\ 1&4&\compose{\circle(18)}{6}&5&\compose{\circle(18)}{2}&&4&1!\/\times\/6 \\ 1&\compose{\circle(18)}{4}&6&5&3&\compose{\circle(18)}{2}&5&0!\/\times\/6 \\ 1&5&\compose{\circle(18)}{2}&\compose{\circle(18)}{3}&&&3&2!\/\times\/6 \\ \compose{\circle(18)}{1}&5&2&\compose{\circle(18)}{4}&&&3&2!\/\times\/6 \\ 1&5&2&6&\compose{\circle(18)}{3}&\compose{\circle(18)}{4}&5&0!\/\times\/6 \\ 1&5&\compose{\circle(18)}{2}&6&\compose{\circle(18)}{4}&&4&1!\/\times\/6 \\ \compose{\circle(18)}{1}&5&\compose{\circle(18)}{3}&&&&2&3!\/\times\/6 \\ 1&5&4&\compose{\circle(18)}{2}&\compose{\circle(18)}{3}&&4&1!\/\times\/6 \\ 1&5&\compose{\circle(18)}{4}&2&\compose{\circle(18)}{6}&&4&1!\/\times\/6 \\ \end{array}$
$\begin{array}{c25c25c25c25c25c25|c30|r50C25} \compose{\circle(18)}{1}&5&4&3&2&\compose{\circle(18)}{6}&5&0!\/\times\/6 \\ 1&5&\compose{\circle(18)}{4}&3&\compose{\circle(18)}{6}&&4&1!\/\times\/6 \\ 1&\compose{\circle(18)}{5}&4&6&\compose{\circle(18)}{2}&&4&1!\/\times\/6 \\ 1&5&4&\compose{\circle(18)}{6}&3&\compose{\circle(18)}{2}&5&0!\/\times\/6 \\ 1&\compose{\circle(18)}{5}&\compose{\circle(18)}{6}&&&&2&3!\/\times\/6 \\ 1&6&\compose{\circle(18)}{2}&\compose{\circle(18)}{3}&&&3&2!\/\times\/6 \\ \compose{\circle(18)}{1}&6&2&\compose{\circle(18)}{4}&&&3&2!\/\times\/6 \\ 1&\compose{\circle(18)}{6}&2&5&\compose{\circle(18)}{3}&&4&1!\/\times\/6 \\ 1&6&\compose{\circle(18)}{2}&5&\compose{\circle(18)}{4}&&4&1!\/\times\/6 \\ \compose{\circle(18)}{1}&6&\compose{\circle(18)}{3}&&&&2&3!\/\times\/6 \\ 1&6&4&\compose{\circle(18)}{2}&\compose{\circle(18)}{3}&&4&1!\/\times\/6 \\ \compose{\circle(18)}{1}&6&4&2&\compose{\circle(18)}{5}&&4&1!\/\times\/6 \\ 1&6&4&\compose{\circle(18)}{3}&2&\compose{\circle(18)}{5}&5&0!\/\times\/6 \\ \compose{\circle(18)}{1}&6&4&3&\compose{\circle(18)}{5}&&4&1!\/\times\/6 \\ 1&6&\compose{\circle(18)}{4}&\compose{\circle(18)}{5}&&&3&2!\/\times\/6 \\ 1&\compose{\circle(18)}{6}&5&\compose{\circle(18)}{2}&&&3&2!\/\times\/6 \\ 1&6&\compose{\circle(18)}{5}&3&4&\compose{\circle(18)}{2}&5&0!\/\times\/6 \\ \compose{\circle(18)}{1}&6&5&\compose{\circle(18)}{4}&&&3&2!\/\times\/6 \\ \end{array}$

In breve, ecco i numeri

$\begin{array}{l|r+50} n|r&1&2&3&4&5&6&7&8&9 \\ \hline 1&1 \\ 2&2&0 \\ 3&3&0&3 \\ 4&8&8&8&0 \\ 5&30&40&35&0&15 \\ 6&144&216&192&120&48&0 \\ 7&840&1344&1302&952&469&0&133 \\ 8&5760&9600&9984&8064&4608&1792&512&0 \\ 9&45360&77760&85320&73440&47250&23256&8469&0&2025 \\ \end{array}$

e il grafico



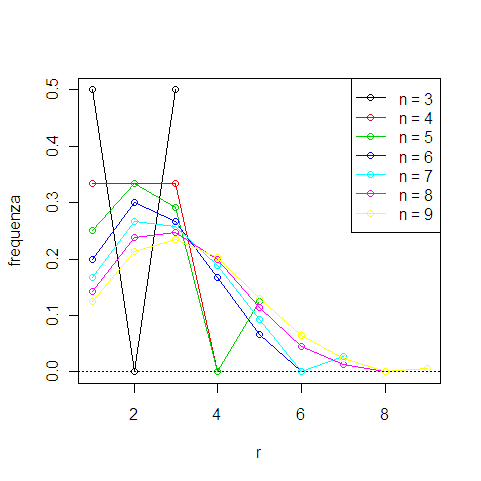
Osserviamo che se non vi sono ultimi o penultimi gradi pari!

[giobimbo]

Il problema è di qualche anno fa e a causa della mia pigrizia nello scrivere, per cui metto giù solo il minimo indispensabile, non ho ricostruito perfettamente la situazione, da cui le incongruenze. Mi son reso conto in questi giorni di aver trascurato dei dati.

Spero di fare meno pasticci con il prossimo problema, che sarà basato sulla mossa del cavallo.