Quattro cerchi in un triangolo

[franco]

Non so se questo è già apparso nel forum:

Consideriamo il triangolo ABC nel quale è inscritto il cerchio C di centro O e disegnamo tre altri cerchi C1, C2 e C3 (di centri rispettivamente O1, O2 e O3) tangenti ciascuno a due lati del triangolo ed al cerchio inscritto.
Se questi ultimi tre cerchi hanno raggio 1, 4 e 9, quanto misura il raggio del cerchio C?

(il disegno è fuori scala e qualche tangente tange poco! )

ciao

[mathmum]

Qualche idea buttata lì, guardando il disegno:
secondo me, a occhio e croce, (bella questa, detta da una mathmum, ma non ho carta e penna o geogebra per farmi un disegno) A, O_1 e O devono essere collineari (proprietà di congruenza dei segmenti di tangente staccati da un punto esterno a una circonferenza), come pure per C, O_3 e O, e così via.
Sempre a occhio e croce la tangente alla circonferenzona è parallela alla base del triangolo, e le altre due sono parallele ai rimanenti lati del triangolo.
Ancora di più a occhio e croce potrei osar dire che il raggio della circonferenzona è la somma dei raggi delle circonferenzine, ma qui ci vuole una dimostrazione (del resto ci vorrebbe anche per le cose che ho detto prima!!!).
Più tardi vedo di procurarmi carta e penna (qui ci sono solo melanzane e peperoni ) e vi faccio sapere se ho detto qualche cavolata di troppo.
Ciao
S.

[franco]

Sulla collinearità di vertici e centri concordo con te (i centri sono sulle bisettrici degli angoli) mentre non sono d'accordo con il parallelismo fra lato e tangenti cerchio/cerchio: queste dovrebbero essere semplicemente perpendicolari alle bisettrici (almeno credo).

In verità mi è venuta una mezza idea ma devo provare a scriverla e soprattuto a fare i conti!

ciao

[panurgo]

Per avere qualche spunto, date un'occhiata qui

[franco]

Per il momento evito di sbirciare "lì" e provo a spiegare come sto procedendo:

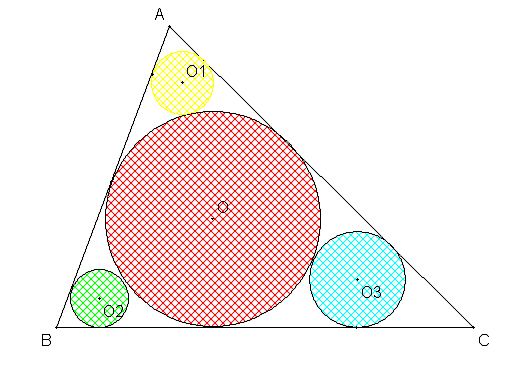
Con riferimento alla figura qui sotto, mi sono concentrato sui triangoli gialli (l'angolo in rosso è retto):


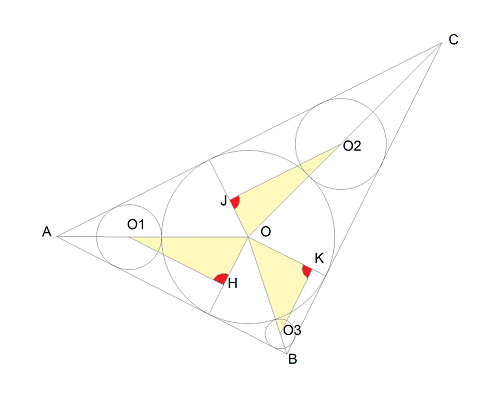
Riferendomi al primo (O1OH) abbiamo che l'ipotenusa è pari alla somma dei raggi dei due cerchi mentre il cateto OH è pari alla differenza fra gli stessi. Inoltre l'angolo in O1 è pari alla metà dell'angolo al vertice A del triangolo originale.
Ripetendo lo stesso ragionamento agli altri due triangolini ottengo il seguente sistema di 4 equazioni con 4 incognite:

${\begin{array} {\sin \frac{\alpha }{2} = \frac{{R - R_1 }}{{R + R_1 }}} \\ {\sin \frac{\beta }{2} = \frac{{R - R_2 }}{{R + R_2 }}} \\ {\sin \frac{\gamma }{2} = \frac{{R - R_3 }}{{R + R_3 }}} \\ {\alpha + \beta + \gamma = \frac{\pi }{2}} \\ \end{array}}$

acc... la graffa non viene e c'è un dollaro che non riesco a far sparire!!

Posso ridurre il sistema sino a questo:
${R = \frac{{1 + \sin \frac{\alpha }{2}}}{{1 - \sin \frac{\alpha }{2}}}}$
${R = 4\frac{{1 + \sin \frac{\beta }{2}}}{{1 - \sin \frac{\beta }{2}}}}$
${R = 9\frac{{1 + \sin \left( {\frac{\pi }{4} - \frac{\alpha }{2} - \frac{\beta }{2}} \right)}}{{1 - \sin \left( {\frac{\pi }{4} - \frac{\alpha }{2} - \frac{\beta }{2}} \right)}}}$

però da qui in avanti i miei ricordi di trigonometria diventano troppo nebulosi.

Se ho tempo provo a risolverlo numericamente (sempre che ci riesca!)
(P.S. se vi accorgete che ho scritto fesserie, avvisatemi prima che mi inoltri un un pantano di calcoli inutili )


ciao

[panurgo]

${\begin{array} {\sin \frac{\alpha }{2} = \frac{{R - R_1 }}{{R + R_1 }}} \\ {\sin \frac{\beta }{2} = \frac{{R - R_2 }}{{R + R_2 }}} \\ {\sin \frac{\gamma }{2} = \frac{{R - R_3 }}{{R + R_3 }}} \\ {\alpha + \beta + \gamma = \frac{\pi }{2}} \\ \end{array}}$

acc... la graffa non viene e c'è un dollaro che non riesco a far sparire!!

tu hai scritto

Codice: Seleziona tutto

[tex]{\begin{array}
   {\sin \frac{\alpha }{2} = \frac{{R - R_1 }}{{R + R_1 }}}  \\
   {\sin \frac{\beta }{2} = \frac{{R - R_2 }}{{R + R_2 }}}  \\
   {\sin \frac{\gamma }{2} = \frac{{R - R_3 }}{{R + R_3 }}}  \\
   {\alpha  + \beta  + \gamma  = \frac{\pi }{2}}  \\
\end{array}}[/tex]

ma, per ottenere

$\left \{ { \sin \frac \alpha 2 = \frac {R - R_1} {R + R_1} \\ \sin \frac \beta 2 = \frac{R - R_2} {R + R_2} \\ \sin \frac \gamma 2 = \frac {R - R_3} {R + R_3} \\ \alpha + \beta + \gamma = \frac \pi 2 } \right.$

dovevi scrivere

Codice: Seleziona tutto

[tex]\left \{ 
  {
    \sin \frac \alpha 2 = \frac {R - R_1} {R + R_1} \\
    \sin \frac \beta 2 = \frac{R - R_2} {R + R_2} \\
    \sin \frac \gamma 2 = \frac {R - R_3} {R + R_3} \\
    \alpha + \beta  + \gamma  = \frac \pi 2 
  }
\right.[/tex]

[franco]

Non c'è voluto moltissimo con il fido excel (pardon, OpenOfficeCalc):
R=11,00
(alfa=112,88°, beta=55,65°, gamma=11,47°)

[franco]

${\begin{array} {\sin \frac{\alpha }{2} = \frac{{R - R_1 }}{{R + R_1 }}} \\ {\sin \frac{\beta }{2} = \frac{{R - R_2 }}{{R + R_2 }}} \\ {\sin \frac{\gamma }{2} = \frac{{R - R_3 }}{{R + R_3 }}} \\ {\alpha + \beta + \gamma = \frac{\pi }{2}} \\ \end{array}}$

acc... la graffa non viene e c'è un dollaro che non riesco a far sparire!!

tu hai scritto


......

Sicuramente hai ragione, in realtà ho scritto le formule su TeXaide e poi le ho importate col copia/incolla ma c'è qualcosa che non quadra: sarà che ho cambiato PC e non ricordo più come andava impostato il traduttore?

ciao

[panurgo]

texaide non è male ma mette tante parentesi e cose che non sono strettamente necessarie...

[franco]

In realtà la cosa che più mi rende ritroso dall'utilizzo del Tex tal quale è la necessità di usare le parentesi graffe, un simbolo che non è presente nella tastiera e non so assolutamente come far apparire!
C'è un modo per "programmare" la tastiera in modo da far apparire le graffe aperte/chiuse ad esempio digitando ctr+alt+q e ctr+alt+w? O in che altro modo si possono digitare?

ciao

[panurgo]

Se hai un Mac non so, se hai un PC:

Alt Gr - è ---> [
Alt Gr - + ---> ]

Alt Gr - Maiusc - è ---> {
Alt Gr - Maiusc - + ---> }

[franco]

{{{ grazie mille }}}

[antonio]

Sono in ferie e non posso allegare il procedimento, ma posso dire, che (senza aver sbirciato ai suggerimenti), il raggio del cerchio inscritto è pari a 11.
Ho provato poi a generalizzare il problema al caso di un quadrilatero circosscrivibile ad una circonferenza, ma mi sono arenato.
A presto!

[antonio]

Preciso con ritardo (dovuto alla mancanza del mio PC) il mio precedente intervento.
Indico con r il raggio del cerchio inscritto nel triangolo e con $r_{1}$, $r_{2}$ e $r_{3}$ i raggi dei tre cerchietti tangenti come indicato.
Su ogni lato del triangolo ho proiettato ortogonalmente i tre centri relativi; mi riferisco ad esempio al lato BC: ho proiettato $O$, $O_{1}$ e $O_{2}$, rispettivamente in $H$, $K$ e $M$.
Ho preso poi in considerazione, sempre per il lato $BC$:
1) i trapezi rettangoli $OHKO_{1}$ e $OHMO_{2}$, calcolandone le altezze $HK$ e $HM$ con Pitagora;
2) i triangoli simili $O_{2}KB$ e $OHB$, da cui ho ricavato $BK$;
3) i triangoli simili $O_{3}MC$ e $OHC$, da cui analogamente ho ricavato $MC$.
Con qualche passaggio ottengo $a=BC=2r\sqr{r}(\frac{\sqr{r_{2}}}{r-r_{2}}+\frac{\sqr{r_{3}}}{r-r_{3}})$.
Analogamente gli altri lati:
$b=AC=2r\sqr{r}(\frac{\sqr{r_{1}}}{r-r_{1}}+\frac{\sqr{r_{3}}}{r-r_{3}})$ e
$c=AB=2r\sqr{r}(\frac{\sqr{r_{1}}}{r-r_{1}}+\frac{\sqr{r_{2}}}{r-r_{2}})$.

Indicando con $p=a+b+c$ il perimetro, ho successivamente calcolato l'area del triangolo prima applicando la formula
$A=\frac{pr}{2}$ e poi tramite la formula di Erone.
Uguagliando le due espressioni ottenute, si ottiene dopo qualche passaggio l'equazione seguente in
$r$, $r_{1}$, $r_{2}$ e $r_{3}$:

$\frac{\sqr{r_{1}}}{r-r_{1}}+\frac{\sqr{r_{2}}}{r-r_{2}}+\frac{\sqr{r_{3}}}{r-r_{3}}=4r\cdot\frac{\sqr{r_{1}}}{r-r_{1}}\cdot\frac{\sqr{r_{2}}}{r-r_{2}}\cdot\frac{\sqr{r_{3}}}{r-r_{3}}$.

Questa equazione generale si può trasformare in un'equazione di II grado, più complicata da scrivere.

Infine, sostituendo a $r_{1}$, $r_{2}$ e $r_{3}$ i valori di 1, 4 e 9, si ottiene $r^{2}-12r+11=0$ da cui $r=1$, non accettabile e $r=11$.

Come detto prima, sarebbe interessante estendere il tutto ai quadrilateri circoscrivibili in una circonferenza.