Circuiti automobilistici

[giobimbo]

Nella figura sotto son disegnate con vista dall'alto due piste, A e B, per automobiline elettriche. Essendoci dei cavalcavia tali piste appaiono come formate da 5 pezzi ciascuna, in figura numerati da 1 a 5 in modo che l'automobilina percorra i tratti visibili dall'alto in ordine numerico, 1, 2, 3, 4 e 5, per poi ricominciare da 1 e così via. Cerchiamo di assegnare a ogni pista una formula matematica che ne riassuma le caratteristiche.

Esaminiamo la pista A. Viaggiando sul tratto 1 a un certo punto passeremo sotto il cavalcavia 4, allora scriviamo $1^4$; usciti da sotto il cavalcavia ci troviamo sul tratto 2 su cui proseguiamo fino a passar sotto il cavalcavia 5, scriviamo $2^5$; ora ci troviamo sul tratto 3 ... ; ci ritroviamo sul tratto 1. Allora:
$\displaystyle pista A = 1^4\, 2^5\, 3^1\, 4^2\, 5^3$
Questa è la notazione normale.
Riscriviamo la sequenza di potenze in altro modo. Se una potenza ha m come esponente allora la potenza successiva sarà quella che ha m come base. Con tale regola risulta:
$\displaystyle pista A = (1^4\, 4^2\, 2^5\, 5^3\, 3^1)$
Questa è la notazione per cicli, alla pista A corrisponde un ciclo unico di 5 elementi.

Esaminiamo la pista B. Percorrendola come già descritto otteniamo la formula:
$\displaystyle pista B = 1^4\, 2^1\, 3^5\, 4^2\, 5^3$ in notazione normale,
$pista B = (1^4\, 4^2\, 2^1)\, (3^5\, 5^3)$ in notazione per cicli. Stavolta abbiamo due cicli, quello generato dal tratto 1 e formato da tre elementi: 1, 2 e 4; quello generato dal tratto 3 e formato dai due elementi 3 e 5.


Sapendo che nella formula di una pista, in notazione normale:
1) ogni base ha un solo esponente (cioè nessun tratto del percorso passa sotto 2 o più cavalcavia),
2) non esiste la potenza $x^x$,
3) dopo la potenza $x^y$ non può esserci la potenza $y^z$ (attenzione, se l'ultima potenza della formula è $u^v$ la prima potenza non può essere $v^w$)
costruire (o scrivere la formula di) una pista che abbia:
a) un ciclo unico di 6 elementi;
b) un ciclo formato dagli elementi 1, 2, 3, 5, 6

[Br1]

Ciao, Giobimbo

Oggi pomeriggio mi sono accorto del tuo
post e stasera, tornando a casa in corriera,
ho buttato giù qualche schema. Quello che
ti riporto qui sotto dovrebbe (dovrebbe)
rispondere al tuo punto a:



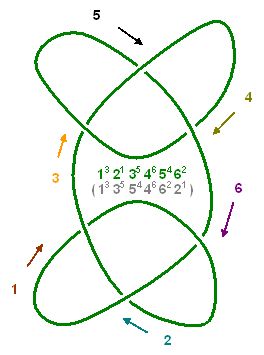
Tra le varie cose, mi è subito saltato fuori uno
schema simpatico con questa formula normale:

$1^8\,2^5\,3^6\,4^3\,5^4\,6^1\,7^2\,8^7\,.$

Mah... non sono tanto sicuro di aver capito
quello che chiedi, ma appena riesco provo a
cercare qualcosa anche per il punto b.

[giobimbo]

Molto, molto bene Br1, è proprio quello il circuito automobilistico desiderato. Immagino che la corriera abbia percorso un bel po' di chilometri, visto che su 20 percorsi teorici possibili solo uno corrisponde ai requisiti del problema.

Tra la tua soluzione e lo schema simpatico con 8 tratti visibili c'è una notevole affinità, in quanto ambedue le piste possono essere tagliate in due posti in modo che, ricongiungendole in modo diverso, formino due piste simili di 3 tratti visibili nel primo caso e di due piste simili di 4 tratti visibili nel secondo. Ciò si può vedere anche analiticamente.
Si ponga un'automobilina sul tratto 1 della figura di Br1 ma si percorra la pista in direzione opposta, otterremo la formula:
$Soluzione di Br1 = (1^6\, 6^5\, 5^1)\, (2^4\, 4^3\,3^2)$ in notazione per cicli. Un ciclo è formato dai tre tratti consecutivi 5, 6 e 1; l'altro dai tre tratti consecutivi 2, 3 e 4; ogni ciclo formerà una pista a forma di trifoglio.
Si costruisca una pista corrispondente allo schema simpatico, si ponga un'automobilina sul tratto 1 ma si percorra la pista in direzione opposta, otterremo stavolta la formula:
$Schema simpatico = (1^3\, 3^1)\, (2^8\, 8^2)\, (4^6\, 6^4)\, (5^7\, 7^5)$ in notazione per cicli. I primi due cicli son formati dai 4 tratti consecutivi 8, 1, 2 e 3; gli altri due cicli hanno i 4 tratti consecutivi 4, 5, 6 e 7. Si unisca il 3 all'8 e il 7 al 4 per ottenere i due minicircuiti simili.

Provo a fare un esempio che chiarisca cosa s'intende col problema b).
Costruire (o scrivere la formula di) una pista che abbia:
c) un ciclo formato dagli elementi 1, 2, 4.
Qual è una soluzione di questo problema c)? La pistaB del mio disegno in alto, che appunto ha un ciclo $(1^4\, 4^2\, 2^1)$ formato dagli elementi 1, 2 e 4.

[Br1]

Il punto b, Giobimbo, mi ha un po'
ossessionato nel fine settimana e
stamattina sono arrivato a questo
schema:



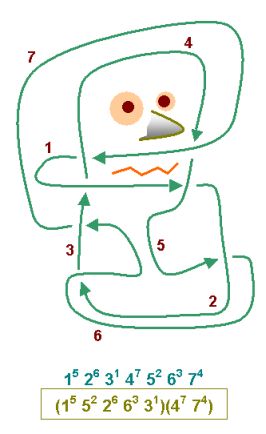
L'ho disegnato in fretta con Excel
e spero di non aver preso qualche
cantonata

Ma qualunque cosa abbia combinato,
Giobimbo, mi sono divertito

[delfo52]

io invece ho avuto problemi con il punto G....
................
...............
...........

[Br1]

...e cioè? $\;$

Ok, ok... ne approfitto per salutarti$\;$

[giobimbo]

Excel-lente, direi!

Ho avuto il tempo di esaminare con cura i circuiti da 6 e da 8 elementi precedentemente trovati, tagliandoli a metà si ottengono due minicircuiti topologicamente equivalenti. Di circuiti a trifoglio ce ne sono due tipi, uno speculare dell'altro, mentre ce n'è uno solo con 4 elementi, speculare di se stesso.