Il recinto

[panurgo]

Nell'ultimo numero di Rudi Mathematici viene proposto il seguente problema: dovendo costruire un recinto con pezzi di materiale lunghi rispettivamente 1, 2, 3 e 4 qual è l'area massima che si riesce ad ottenere.

Mi ricordo vagamente che un argomento simile è stato discusso o proposto anche qui ma non sono riuscito a trovarlo

Lo abbiamo davvero già discusso? E se no, perché non discuterlo ora?

[Admin]

Ciao panurgo,
in effetti ricordi bene, la discussione si intitolava "monotremi" e riguardava il ben noto problema proposto a suo tempo da Enrico (http://utenti.quipo.it/base5/analisi/ornitorinchi.htm" onclick="window.open(this.href);return false;);
dunque, la discussione ce l'ho in locale (grazie al mitico Peppe, ovviamente);
dovrei reinserirla sul forum; appena posso la inserisco.

Nel frattempo ti riporto alcune risposte estratte dalla discussione:

La soluzione suggerita da delfo52 (caffettiera moka) ha una lunghezza minima complessiva di circa 3,951258. (salvo errori)
Secondo me la soluzione migliore comporta, al posto dei quattro segmenti laterali, l'utilizzo di quattro archi di cerchio.

o non ho fatto i conti, ma concordo con MaMo: credo che le linee che collegano alla circonferenza debbano essere perpendicolari a quest'ultima, come credo anche che si uniscano al tratto di segmento formando un angolo (anzi:3) di 120°.
Tutto questo in analogia con le bolle di sapone e facendo piccoli ragionamenti di natura "infinitesimale": basta pensare che se così non fosse si potrebbe deformare leggermente in un intorno del nodo delle tre linee accorciando la lunghezza complessiva senza cambiare la superficie (ma spiegare come "a voce" non è affatto facile).

Ho verificato l'ipotesi di infinito.
Per la configurazione proposta ho trovato una lunghezza complessiva di circa 3,945703.

I risultati da me trovati si riferiscono ad un cerchio di raggio 1, cioè equiuvalgono al rapporto L/r.

Ciao
Admin

[peppe]

Confermo!
Trascrivo il testo del quesito:

Inviato: Dom Giu 12, 2005 6:27 pm Oggetto: monotremi

Chiedo anticipatamente scusa per l'egocentrismo;
in una scorribanda nell'archivio storico delle ricreazioni di Base5, mi è tornato sotto gli occhi un quesito che proposi tempo addietro. Con le nuove potenzialità della nuove veste grafica potrebbe essere interessante tornare ad interessarsi del
Recinto degli ornitorinchi.
Non sono ahimè in grado di fare quelle strane cose tipo copia-incolla o diavolerie simili, ma rimando gli interessati all'archivio citato. Basta immettere come parola chiave "ornitorinchi" e vedrete (qualcuno forse lo ricorderà) il problema che consiste nel trovare la suddivisione di una superficie circolare in quattro parti equiestese, senza la formazione di punti di incontro della rete "a quattro". GF Bo fece già in epoca preistorica dei disegni interessanti,mma adesso, chi si vuole scatenare...
Enrico

delfo52.

[Pasquale]

Mi pare che si tratti di due problemi diversi. In questo bisogna trovare il quadrilatero irregolare di area maggiore.

[panurgo]

Mi pare che si tratti di due problemi diversi. In questo bisogna trovare il quadrilatero irregolare di area maggiore.

Esatto! Questo problema può essere enunciato così: dati quattro segmenti lunghi rispettivamente 1, 2, 3 e 4 costruire il quadrilatero di area massima.

[Sancho Panza]

Salve,
da quando vi siete trasferiti sul nuovo forum mi risulta assai più difficile collegarmi al Forum.

Riguardo al problema del quadrilatero,
non scrivo la mia soluzione (per ora) per rispetto dei lettori di RM;
ma vi anticipo che il raggio del cerchio in cui risulta inscritto il quadrilatero di area massima è uguale a: $\frac{{\sqrt {2310} }}{{24}}$



Hasta luego,
Sancho Panza

[franco]

Concordo con la scelta di Sancho,
Almeno sino alla pubblicazione del prossimo numero di RM credo che dovremmo evitare di postare delle soluzioni (ne ho trovata una anch'io ma non ho potuto verificare se coincide con quella di Sancho, ho sicuramente approcciato il problema in modo diverso).
Magari ne discutiamo dopo.

ciao

[Quelo]

Analiticamente parlando è fuori dalla mia portata, ma con qualche esperimento geometrico (o meglio geogebrico) ho ricavato che il raggio della circonferenza circoscritta è uguale a 2,0026 (aumentando il livello di precisione compare qualche decimale).

Ma perché? Un quadrilatero irregolare è sempre inscrivibile in una circonferenza?

Il quadrilatero in questione sembrerebbe inscrivibile in una circonferenza. (Risposta retroattiva)

[Pasquale]

Ma perché? Un quadrilatero irregolare è sempre inscrivibile in una circonferenza?
Intanto, mi sento di affermare che la ricerca può essere limitata a due soli tipi di quadrilatero, quali ad esempio, procedendo in senso orario: 1,2,4,3 - 1,3,2,4.
Essendo trascorso del tempo, anticiperei inltre che l'area massima si ottiene in ambedue i casi e si aggira intorno a 4.8989794855.....

[panurgo]

Anche se non è ancora uscito il nuovo numero di RM penso che possiamo postare le nostre idee.

Pasquale, prova a dare un'occhiata al 339

[franco]

Forse chiamarla "soluzione" è eccessivo, ma questo è quanto sono stato in grado di fare, nei piccolissimi ritagli di tempo che in questo periodo posso dedicare alle ricreazioni:



ciao

[Pasquale]

Ah si, grazie Pan, non ancora avevo realizzato che gli angoli opposti fossero supplementari (nel senso che non avevo fatto la somma di $\text\alpha e \beta$, di cui a quanto segue.



Si, anch'io mi sono appoggiato alla diagonale "a" (mi accorgo che nel disegno non l'ho etichettata).
Ho pensato che nei due triangoli che si ottengono, al variare della diagonale (1<a<3), si modifica la figura e variano le loro aree e dunque la loro somma.

In sostanza ho calcolato l'area del quadrilatero in funzione della diagonale.

Quindi, applicando noti teoremi trigonometrici:

$a^2=1^2+2^2-4cos\alpha =5-4cos\alpha\\a^2=3^2+4^2-24cos\beta=25-24cos\beta$

da cui

$cos\alpha=\frac {5-a^2}{4}\\cos\beta=\frac{25-a^2}{24}$

L'area dei due trangoli è data da:

$S_1=\frac{1\cdot 2}{2}sen\alpha=sen\alpha\\S_2=\frac{3\cdot 4}{2}sen\beta=6sen\beta$

l'area del quadrilatero:

$S=s_1+s_2 =sen\alpha+6sen\beta=\sqrt{1-cos^2\alpha}+6\sqrt{1-cos^2\beta}=\frac{1}{4}\(\sqrt{10a^2-a^4-9}+\sqrt{50a^2-a^4-49}\)$

Imponendo i due radicandi come positivi, si verifica che 1<a<3 (escludendo i valori limite di 1 e 3).

Derivando l'area ed eguagliandola a zero, si perviene all'equazione risolutiva

$a^2(7a^4-62a^2+55)=0$

fra le cui soluzioni, l'unica accettabile assume il valore di

a=2,803059552906941

da cui:

$cos\alpha=\frac{5-a^2}{4}=-0,714285714285715$

\alpha=135°,584691402807

cos\beta=\frac{25-a^2}{24}=0,714285714285715

\beta=44°,415308597193

S=sen\alpha+6sen\beta=4,89897948556636

Con le altre configurazioni, si perviene allo stesso risultato.
Il procedimento è un po’ laborioso e se interessa solo il risultato, si può velocizzare il calcolo con un piccolo programma in Decimal Basic:

OPTION ANGLE DEGREES
LET i=10^(-5)
LET mas=0
FOR a=1 TO 3 STEP i
LET cosa=(5-a^2)/4
LET cosb=(25-a^2)/24
LET s1=SQR(1-cosa^2)
LET s2=6*SQR(1-cosb^2)
LET s=s1+s2
IF s>=mas THEN
LET mas=s
LET b=a
END IF
NEXT A
PRINT "diagonale=";b
PRINT "alfa=";ACOS((5-b^2)/4)
PRINT "beta=";ACOS((25-b^2)/24)
PRINT "area massima=";mas
END


In una seconda passata, si può migliorare l’approssimazione, diminuendo la i e restringendo il campo di calcolo per valori di a fra 2,80 e 2,81; con altri lanci si può affinare sempre di più il risultato, procedendo in tal modo molto più velocemente.
Inserendo un PRINT nel ciclo condizionato, si può vedere come varia l'area al variare di a.

[panurgo]

Ecco la mia risposta... (G. Verdi, Falstaff)

La via normale per la risoluzione di un problema di massimo passa per la definizione della quantità che si vuole massimizzare in funzione di un parametro, per il calcolo della derivata e l'estrazione delle radici dell'equazione algebrica ottenuta eguagliando tale derivata a zero; ed è quello che ho cominciato a fare mentalmente mentre leggevo l'enunciato del problema: ho immaginato il recinto



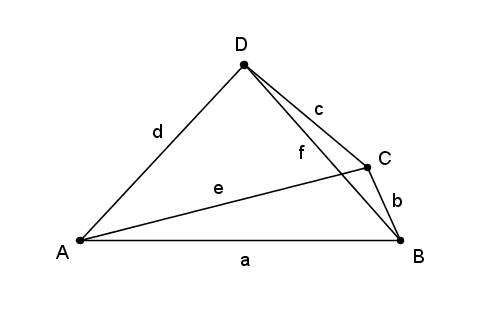
ho scelto come parametro la diagonale $e$ (niente angoli; sono allergico alle graminacee e alla trigonometria e ambedue spuntano, ahimé, dappertutto) e ho espresso l'area mediante la formula di Erone

$A \/ = \/ \sqrt{p \/ \left (p \/ - \/ a \right) \left (p \/ - \/ b \right) \left (p \/ - \/ e \right)} \/ + \/ \sqrt{q \/ \left (q \/ - \/ c \right) \left (q \/ - \/ d \right) \left (q \/ - \/ e \right)}$

con $p$ e $q$ semiperimetri dei triangoli ${\text ABC}$ e ${\text ACD}$ rispettivamente.
A questo punto ho esitato: non ardevo dalla voglia di affrontare tutta quell'algebra, una via normale alquanto noiosa. D'altra parte, prendere la funivia (Mathematica) per arrivare in cima mi pareva poco sportivo e mi sono detto: "perché non prendere la cresta ovest?": mi sono divertito di più nonostante un passaggio più complicato del previsto di cui parlerò a tempo debito.
Intanto mi ero reso conto che l'enunciato del problema tace l'ordine con cui sono disposti i lati del recinto e quindi vi sono sei recinti distinti. Sei? Sei! Le permutazioni di quattro oggetti sono ventiquattro ma, dato che il recinto è chiuso, il primo lato può essere scelto arbitrariamente: una scelta diversa corrisponde ad una rotazione del recinto, per esempio $\left \{1234, \/ 2341, \/ 3412, \/ 4123 \right \}$, ed è evidente che le proprietà di questo recinto non possono dipendere da quale lato decido di considerare per primo.
Quindi ho scelto di cominciare dal lato lungo $4 \/ \text m$, sia per comodità di disegno sia perché... è il più pesante da spostare, e ho considerato il recinto $4|123$ (la barra verticale ricorda che il $4$ resterà sempre al suo posto): ho quindi scambiato tra loro i lati $2$ e $3$ ottenendo il recinto $4|132$



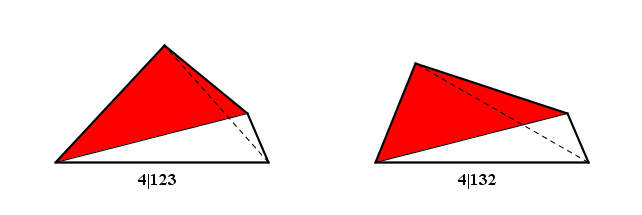
L'area dei due recinti è uguale poiché il triangolo ${\text ABC}$ è rimasto tal quale e il triangolo ${\text ACD}$ ha subìto una riflessione rispetto all'asse della diagonale $e$.
Con questo nuovo recinto ho cambiato diagonale e ho scambiato tra loro i lati $1$ e $3$: il recinto che ho ottenuto ($4|312$) è anch'esso equiesteso per lo stesso motivo di prima



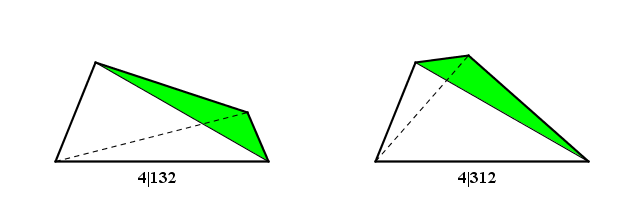
A questo punto mi è parso evidente che l'area massima dei sei recinti dovesse essere la stessa perché ciascuno di essi è ottenibile dagli altri con permutazioni di lati che conservano l'area.
Ho ripetuto il giochetto con l'ultimo recinto (sempre cambiando diagonale) scambiando i lati $1$ e $2$ e ottenendo il recinto $4|321$



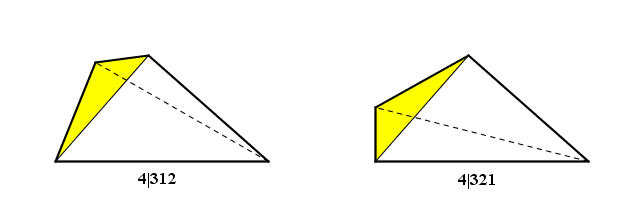
Quest'ultimo recinto differisce dal primo ($4|123$) solo per il verso con cui si incontrano i lati ruotando il recinto e non per le loro posizioni relative: confrontiamoli



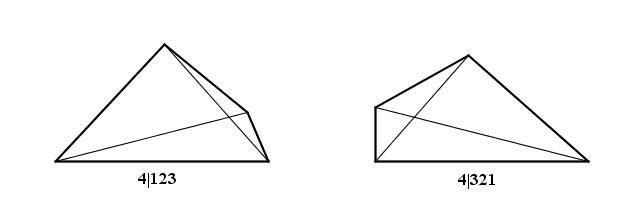
I due recinti hanno area uguale ma diagonali diverse: l'area può essere ottenuta in due modi quindi non è massima.
L'area sarà massima solo se l'applicazione delle permutazioni porta ad un $4|321$ che sia l'immagine speculare del $4|123$ di partenza



Lo stesso vale per le altre permutazioni



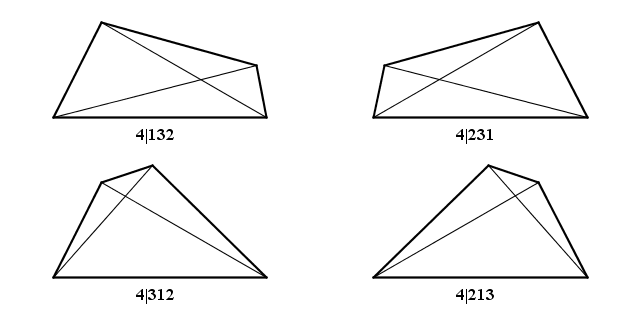
A questo punto, mi sarei potuto accontentare di costruire il recinto massimo per approssimazioni successive, a partire dal recinto $4|123$ con un angolo retto in $\text B$, permutando coppie di lati sino ad ottenere il recinto $4|321$



riportando poi il simmetrico del punto $\text C$ di $4|123$ rispetto all'asse del lato di $4 \/ \text m$ e trovando il nuovo vertice come intersezione della bisettrice con l'arco



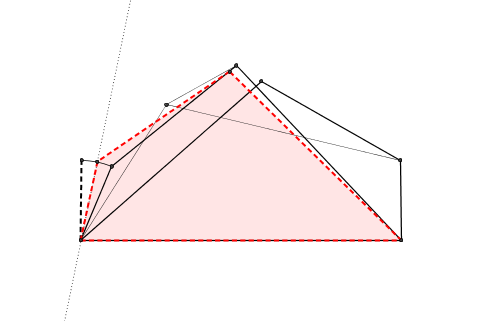
Iterando questo processo si può ottenere l'approssimazione che si desidera: è opportuno notare, tuttavia, che il recinto che si ottiene al primo passaggio ha un'area che differisce dall'area massima meno di tre parti per milione.
Mi sarei potuto accontentare, dunque. Ma chi ama la montagna sa che è più bello arrivare in cima: è quello che ho cercato di fare io sovrapponendo i sei recinti (con una nuova nomenclatura)



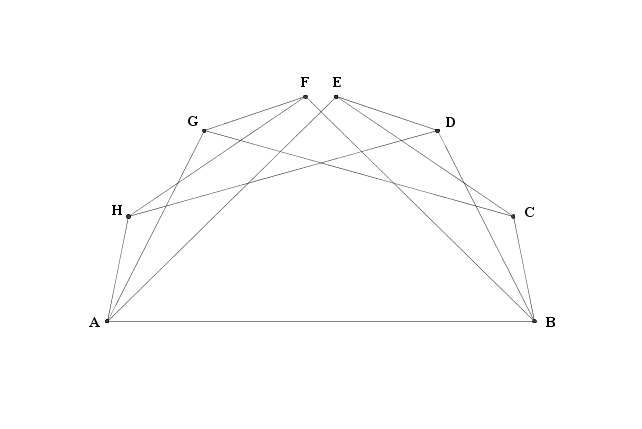
Ho diviso i vertici in due gruppi, ${\text AFGH}$ e ${\text BCDE}$, osservando che essi sono i vertici di due trapezi isosceli che hanno lati obliqui uguali a $1$ e diagonali uguali a $2$



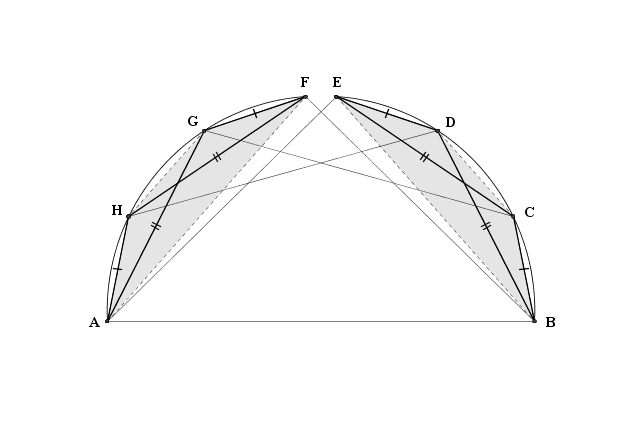
Quindi, i quattro punti di ciascun gruppo appartengono ad un arco di cerchio.
Ho considerato poi il quartetto ${\text ADEH}$: anche questi punti sono i vertici di un trapezio isoscele (lati obliqui, $1$, diagonali, $3$)



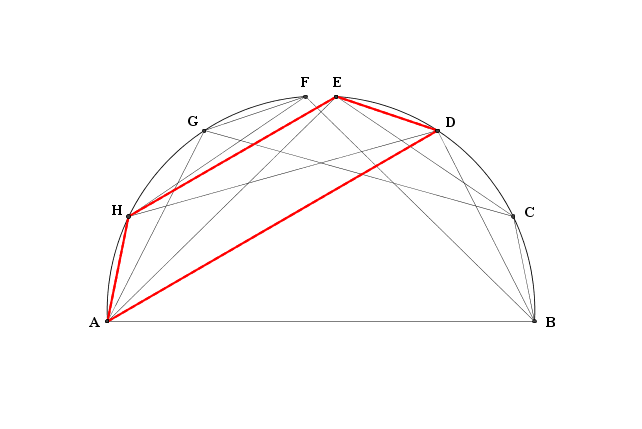
Vi sono infiniti modi di ruotare il trapezio in modo tale che il punto $\text A$ vada a finire in $\text G$, per esempio così



o così



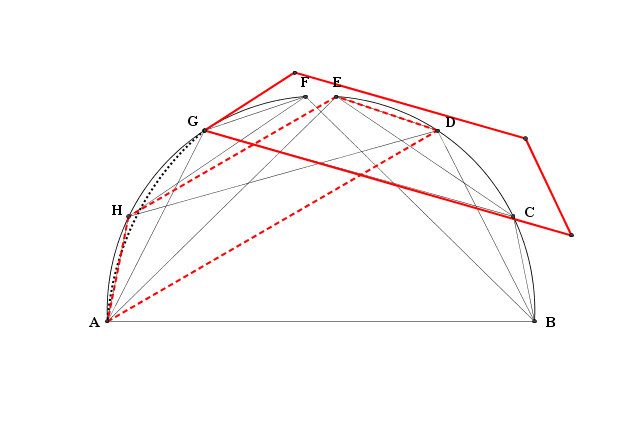
ma vi è un'unica rotazione che mandi anche $\text H$ in $\text F$ ed è quella effettuata intorno al centro dell'arco ${\text FGHA}$



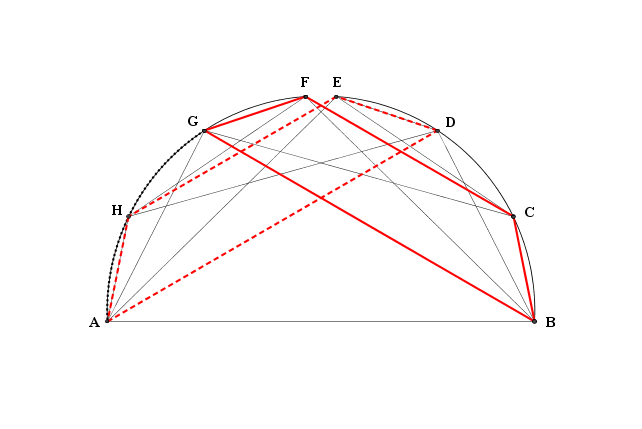
Ma, attenzione! Anche i punti $\text D$ e $\text E$ sono andati a finire rispettivamente in $\text B$ e $\text C$, e l'unica rotazione che sortisce questo effetto è quella intorno al centro dell'arco ${\text BCDE}$: i due archi di cerchio devono appartenere alla stessa circonferenza. Oplà, tutti i recinti, oltre ad essere equiestesi, sono anche conciclici (coinscritti?).
Ho scelto dunque uno dei nostri recinti: uno a caso, $4|123$



Ho applicato il teorema del coseno

$e^{\script 2} \/ = \/ a^{\script 2} \/ + \/ b^{\script 2} \/ - \/ 2 \/ a \/ b \/ \cos \beta \/ = \/ c^{\script 2} \/ + \/ d^{\script 2} \/ - \/ 2 \/ c \/ d \/ \cos \delta$

e, tenuto conto del fatto che in un quadrilatero ciclico gli angoli opposti sono supplementari, ho ottenuto

$\cos \beta \/ = \/ \frac {a^{\script 2} + b^{\script 2} - c^{\script 2} - d^{\script 2}} { 2 \left ( ab + cd \right ) }$

e, dopo le opportune sostituzioni e semplificazioni

$e \/ = \/ \sqrt{ \frac { \left ( ac + bd \right ) \left ( ad + bc \right ) } { ab + cd }} \/ = \/ \sqrt {\frac {11 \times 14} {10}} \/ = \/ \sqrt {\frac {77} {5}}$

e, sostituendo i valori di $a$, $b$, $c$, $d$ ed $e$ nella formula iniziale, ho ottenuto $A = \sqrt {24}$.
Mi permetto a questo punto una piccola digressione sulla formula di Erone. Qualcuno l'ha definita "insulsa"; a me è sempre stata fortemente antipatica e solo dopo aver lavorato su questo problema ho capito il perché: si chiama "Formula di Erone" e non "teorema di Erone" perché non è fatta per spiegare o dimostrare, ma per stupire. Ecco il motivo di quella $p$, che nasconde la vera natura (geometrica) della formula.
Invece di

$A \/ = \/ \sqrt { p \/ \left (p \/ - \/ a \right) \left (p \/ - \/ b \right) \left (p \/ - \/ c \right) }$

scrivo

$A \/ = \/ \sqrt { \frac {\left ( a + b + c \right)} 2 \times \frac { \left (- a + b + c \right)} 2 \times \frac{ \left (a - b + c \right)} 2 \times \frac { \left (a + b - c \right)} 2 } \\ \qquad = \/ \frac 14 \/ \sqrt { \left \[ \left (a \/ + \/ b \right ) \/ + \/ c \right \] \left \[ \left (a \/ + \/ b \right ) \/ - \/ c \right \] \times \left \[ c \/ + \/ \left (a \/ - \/ b \right ) \right \] \left \[ c \/ - \/ \left (a \/ - \/ b \right ) \right \] } \\ \qquad = \/ \frac { \sqrt { \left ( a + b \right )^{\script 2} - c^{\script 2}}} 2 \/ \times \/ \frac {\sqrt {c^{\script 2} - \left ( a - b \right )^{\script 2}}} 2$

ecco che l'area è ottenuta come prodotto di due lunghezze anziché come radice di un quarto grado; e, guardando queste lunghezze, osservo che sono la metà dei secondi cateti di due triangoli rettangoli: il primo ha per ipotenusa $a \/ + \/ b$, cioè il massimo valore che $c$ può assumere; il secondo ha come primo cateto $\left | a \/ - \/ b \right |$, cioè il minimo valore che $c$ può assumere.
Geometricamente, dato il triangolo $\text{ABC}$ riporto $c$ sulla perpendicolare di $a$, trovo il punto $\text D$ sul prolungamento di $a$, distante $a \/ + \/ b$ da $\text A^{\script \prime}$ e, tracciando la tangente ad un cerchio di raggio pari a $\left | a \/ - \/ b \right |$, trovo il punto $\text E$



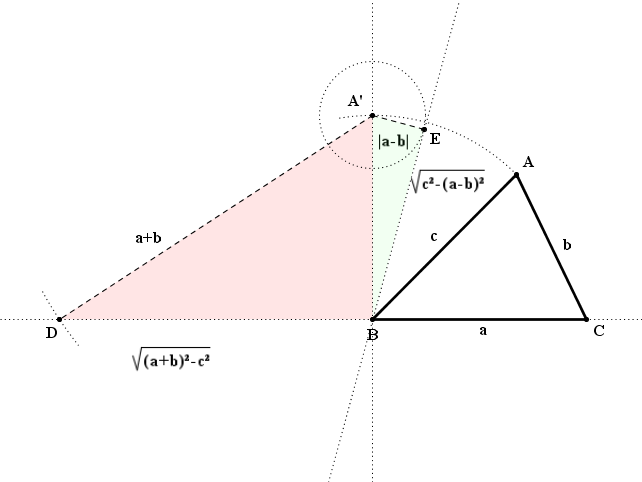
Riporto sul prolungamento di $a$ il punto medio del segmento $\overline{\text BD}$ e, sulla perpendicolare, il punto medio del segmento $\overline{\text BE}$ e costruisco un rettangolo che ha area uguale a quella del triangolo di partenza



Ecco a voi il "rettangolo di Erone"!
Un'ulteriore curiosità: se sono dati i lati $a$ e $b$, l'area del triangolo è massima quando il triangolo è rettangolo, cioè quando

$c^{\script 2} \/ = \/ a^{\script 2} \/ + \/ b^{\script 2} \qquad \Longrightarrow \qquad \left (a \/ + \/ b \right )^{\script 2} \/ - \/ c^{\script 2} \/ = \/ c^{\script 2} \/ - \/ \left (a \/ - \/ b)^{\script 2} \/ = \/ 2ab$

e il rettangolo di Erone è un quadrato.
Questo ci fornisce un mezzo per costruire un segmento che sia la radice quadrata di un segmento dato $a$: è sufficiente costruire il rettangolo di Erone di un triangolo rettangolo di base $a$ e di altezza $2$.



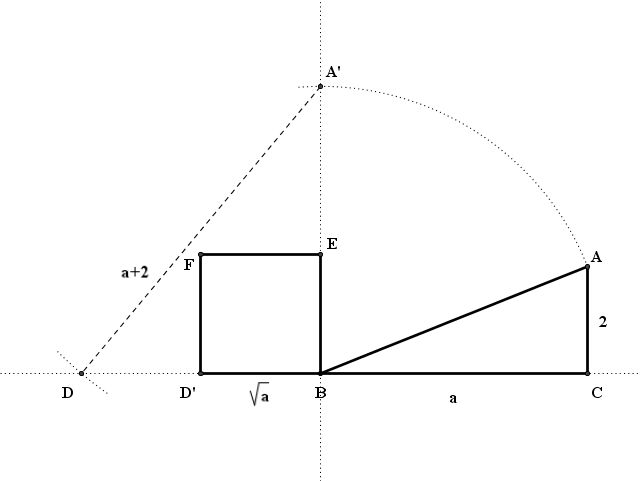
L'area del quadrato è $a$ e il suo lato è $\sqrt{a}$.
A questo punto, se avete letto tutto senza sentire la necessità di sollevare obiezioni è utile che io discuta la difficoltà cui accennavo all'inizio e cioè l'uso della (consideriamola una "nozione comune"?) unicità del massimo.
Non so se vi sia mai capitato di trovarvi in un punto del cammino che sembra facile ma, all'improvviso, si rivela franoso e sdrucciolevole: ho provato un certo brivido quando ho realizzato che assumevo l'unicità del massimo senza prove. Mi ci sono arrovellato sopra per un po' ma una dimostrazione geometrica si è rivelata al di là delle mie forze; sono quindi stato costretto a deviare in parete ricorrendo ai chiodi a pressione e alle scalette dell'analisi.
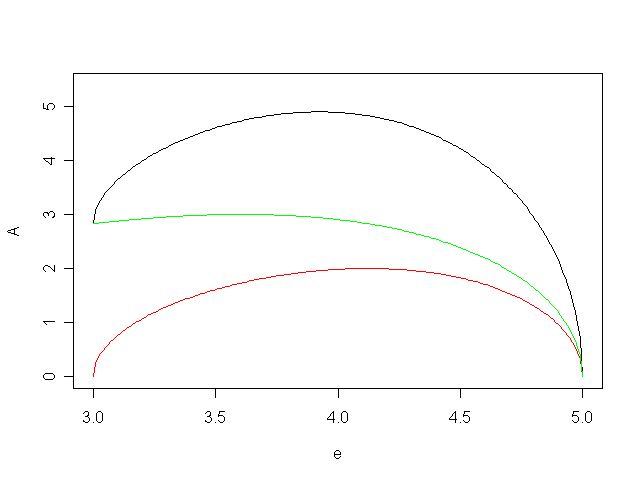
Ho riconsiderato la formula di Erone e ho osservato che si tratta di una funzione concava del terzo lato $c$: in figura è riportata la funzione per rapporti tra i lati $a$ e $b$ corrispondenti a $1:1$, $9:10$, $4:5$, $7:10$ ecc.



Ho considerato $a \/ \geq \/ b$ senza perdita di generalità perché i lati sono permutabili senza variazione di area.
Poiché ero interessato alla forma della curva, ho riscalato i domini e i codomini delle funzioni in modo da farli coincidere; chiaramente, poiché il massimo si ha quando $c^{\script 2} \/ = \/ a^{\script 2} \/ + \/ b^{\script 2}$, al diminuire del rapporto $a/b$ la curva diviene via via più simmetrica con $c_{\script {\text max}} \/ \approx \/ a$.
La funzione che definisce l'area del recinto è la somma di due funzioni concave, quindi è concava anch'essa e ha un massimo unico (la derivata seconda è la somma delle derivate seconde che sono entrambe negative ed è quindi negativa). Ovviamente la funzione

$Q \left (e \right ) \/ = \/ T_{\script 1} \left ( e \right ) \/ + \/ T_{\script 2} \left ( e \right )$

è definita in un dominio che è l'intersezione dei domini di $T_{\script 1}$ e $T_{\script 2}$

$\max \left \{ \left |a \/ - \/ b \right |, \/ \left |c \/ - \/ d \right | \right \} \/ \leq \/ e \/ \leq \/\ \min \left \{ a \/ + \/ b, \/ c \/ + \/ d \right \}$

Nel caso del recinto $4|123$ abbiamo $3 \/ \leq \/ e \/ \leq \/ 5$

[Gianfranco]

Panurgo!
Ho letto (per ora solo una volta) la tua risoluzione, devo ancora capirne bene tutti i particolari, ma ti faccio comunque i miei complimenti!

Davvero un bel lavoro, che deve esserti costato molto tempo, anche per i disegni.

Aggiungo i miei complimenti anche agli altri intervenuti che sono giunti a risultati simili al tuo.

Gianfranco