intersezione di circonferenze
Moderatori: Gianfranco, Bruno
Questo forum è una sezione del PORTALE DI BASE CINQUE
Re: intersezione di circonferenze
Questo nuovo problema è indeterminato nei termini in cui è stato posto! Occhio che l'ellisse non ha la stessa simmetria della circonferenza...
il panurgo
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
Re: intersezione di circonferenze
Umh, la tua obiezione non mi è chiara.
Almeno per quanto riguarda la prima parte la soluzione per quanto essa sia un po' più macchinosa che con il caso dei circoli la si può trovare (a meno di una qualche svista).
Se invece ti riferisci alla seconda parte (quella riferita all'angolo per intenderci) non ci ho ancora ragionato sopra poichè era una curiosità che mi è venuta mentre postavo e non ho potuto dedicarci troppo tempo in quanto sono dovuto tornare ad occuparmi di mia figlia (e delle strutture algebriche).
P.S. non riesco a postare il disegno fatto con geogebra come si fa?
Almeno per quanto riguarda la prima parte la soluzione per quanto essa sia un po' più macchinosa che con il caso dei circoli la si può trovare (a meno di una qualche svista).
Se invece ti riferisci alla seconda parte (quella riferita all'angolo per intenderci) non ci ho ancora ragionato sopra poichè era una curiosità che mi è venuta mentre postavo e non ho potuto dedicarci troppo tempo in quanto sono dovuto tornare ad occuparmi di mia figlia (e delle strutture algebriche).
P.S. non riesco a postare il disegno fatto con geogebra come si fa?
Ah, se i portieri avessero sulla maglia: $|e^{-i\pi}|$...
Pongo $y = x^{2}$ quindi $y=\frac {x^{2}}{pongo}$
[tratto da un compito in classe di uno studente di prima superiore]
Il vero gnomone aureo: http://thumbs.dreamstime.com/z/gnomo-de ... 526933.jpg
Pongo $y = x^{2}$ quindi $y=\frac {x^{2}}{pongo}$
[tratto da un compito in classe di uno studente di prima superiore]
Il vero gnomone aureo: http://thumbs.dreamstime.com/z/gnomo-de ... 526933.jpg
Re: intersezione di circonferenze
Due punti nel piano determinano un segmento; un segmento nel piano può essere il raggio di un cerchio: quindi due punti nel piano determinano due cerchi a seconda di quale dei due è il centro.

Tutto ciò è indipendente dall’orientamento del segmento congiungente i due centri, data la simmetria del cerchio

L’ellisse è simmetrica solo rispetto a due assi ortogonali; due punti determinano infiniti ellissi in quanto ne servono tre per ciascuno di essi: i due fuochi e un punto sull’ellisse stesso

Presumo che, nella tua intenzione, la domanda fosse: dati due ellissi, i cui fuochi giacciono sulla stessa retta, con i due fuochi prossimali giacenti ciascuno sull’altra ellisse, qual è l’area dell’intersezione?
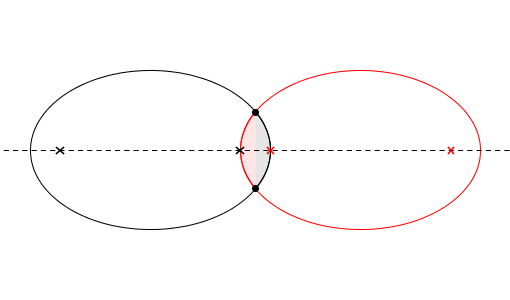
Per il principio di Cavalieri, la “mandorla elissoidale” ${\text E}$ sta alla “mandorla circolare” ${\text C}$ come l’ellisse sta al cerchio
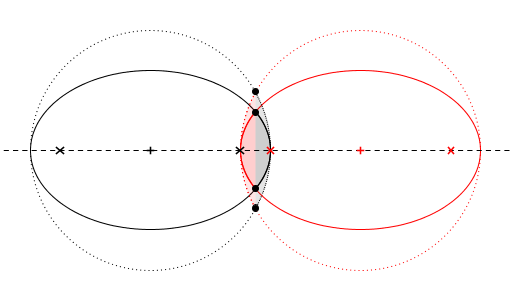
cioè ${\text E}\/=\/\sqrt{k}\/{\text C}$ dove $k$ è il rapporto tra semiasse minore e semiasse maggiore dell’ellisse (se c’ho capito qualcosa ...)
...)

Tutto ciò è indipendente dall’orientamento del segmento congiungente i due centri, data la simmetria del cerchio

L’ellisse è simmetrica solo rispetto a due assi ortogonali; due punti determinano infiniti ellissi in quanto ne servono tre per ciascuno di essi: i due fuochi e un punto sull’ellisse stesso

Presumo che, nella tua intenzione, la domanda fosse: dati due ellissi, i cui fuochi giacciono sulla stessa retta, con i due fuochi prossimali giacenti ciascuno sull’altra ellisse, qual è l’area dell’intersezione?

Per il principio di Cavalieri, la “mandorla elissoidale” ${\text E}$ sta alla “mandorla circolare” ${\text C}$ come l’ellisse sta al cerchio

cioè ${\text E}\/=\/\sqrt{k}\/{\text C}$ dove $k$ è il rapporto tra semiasse minore e semiasse maggiore dell’ellisse (se c’ho capito qualcosa
il panurgo
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
Re: intersezione di circonferenze
Si, infatti intendevo proprio quella coppia di ellissi poiche premettevo la sostituzione dei due circoli con due ellissi "paro paro", tuttavia effettivamente non sono stato abbastanza chiaro nell'esporlo.
Cmq io penna carta e penna alla mano avevo ottenuto una formula molto più complessa della tua (e probabilmente sbagliata) che metteva la "mandorla elissoidale" proprio in funzione dei due semiassi e dell'angolo formato dal semiasse maggiore e dal segmento passante per il centro dell'ellisse e il punto a dintersezione tra le 2 ellissi senza passare dalle circonferenze circoscritte delle ellissi.
P.S. "a lume di naso" direi che la condizione che le due ellissi, con i fuochi che giacciono sulla stessa retta, con i due fuochi prossimali giacenti ciascuno sull’altra ellisse sia una condizione sufficiente perchè le due ellissi siano congruenti.
P.S.S. Con cosa hai fatto il disegno? Se l'hai fatto con geogebra mi spieghi (magari in pm) come si pubblica sul forum?
Cmq io penna carta e penna alla mano avevo ottenuto una formula molto più complessa della tua (e probabilmente sbagliata) che metteva la "mandorla elissoidale" proprio in funzione dei due semiassi e dell'angolo formato dal semiasse maggiore e dal segmento passante per il centro dell'ellisse e il punto a dintersezione tra le 2 ellissi senza passare dalle circonferenze circoscritte delle ellissi.
P.S. "a lume di naso" direi che la condizione che le due ellissi, con i fuochi che giacciono sulla stessa retta, con i due fuochi prossimali giacenti ciascuno sull’altra ellisse sia una condizione sufficiente perchè le due ellissi siano congruenti.
P.S.S. Con cosa hai fatto il disegno? Se l'hai fatto con geogebra mi spieghi (magari in pm) come si pubblica sul forum?
Ah, se i portieri avessero sulla maglia: $|e^{-i\pi}|$...
Pongo $y = x^{2}$ quindi $y=\frac {x^{2}}{pongo}$
[tratto da un compito in classe di uno studente di prima superiore]
Il vero gnomone aureo: http://thumbs.dreamstime.com/z/gnomo-de ... 526933.jpg
Pongo $y = x^{2}$ quindi $y=\frac {x^{2}}{pongo}$
[tratto da un compito in classe di uno studente di prima superiore]
Il vero gnomone aureo: http://thumbs.dreamstime.com/z/gnomo-de ... 526933.jpg
Re: intersezione di circonferenze
fabtor ha scritto:[...]
P.S.S. Con cosa hai fatto il disegno? Se l'hai fatto con geogebra mi spieghi (magari in pm) come si pubblica sul forum?
Generalmente io trasformo l'immagine.png in formato.gif e la inserisco come allegato, ma credo si possa inserire anche in formato.png cliccando sul tasto "Img" (che si trova sopra il corpo del messaggio) per inserire l'url e cliccando prima sulla scritta "Clicca qui", (che trovi proprio sotto il corpo del messaggio) specifica per caricare un'immagine.
Forse sarebbe opportuno aprire in questo forum una filiera specifica... Che cosa ne dite?

"L'essenza della matematica è la libertà" (Georg Cantor)
Re: intersezione di circonferenze
Sotto la finestra dove si inseriscono i messaggi ci sono due righe
Sulla scrittura di espressioni: Promemoria dei simboli
Per caricare un'immagine: Clicca qui
Tu "clicchi lì" e fai l'upload dell'immagine: il nome dell'immagine non deve essere troppo lungo (io ho deciso di far iniziare i nomi di tutte le mie immagini con "panurgo" per renderle identificabili) .
Dopo aver fatto l'upload dell'immagine inserisci il codice
Per esempio, inserisco
e ottengo

P.S.: il disegno è fatto con GeoGebra ed esportato come file "png" che è un formato molto leggero utile per il web...
Sulla scrittura di espressioni: Promemoria dei simboli
Per caricare un'immagine: Clicca qui
Tu "clicchi lì" e fai l'upload dell'immagine: il nome dell'immagine non deve essere troppo lungo (io ho deciso di far iniziare i nomi di tutte le mie immagini con "panurgo" per renderle identificabili) .
Dopo aver fatto l'upload dell'immagine inserisci il codice
Codice: Seleziona tutto
[img]https://www.base5forum.it/upload/nomeimmagine.est[/img]Per esempio, inserisco
Codice: Seleziona tutto
[img]https://www.base5forum.it/upload/panurgoInterElli05.png[/img]e ottengo

P.S.: il disegno è fatto con GeoGebra ed esportato come file "png" che è un formato molto leggero utile per il web...
il panurgo
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
Re: intersezione di circonferenze
Ok grazie mille Pan, appena c'è l'opportunità provo a vedere di riuscirci.
Ah, se i portieri avessero sulla maglia: $|e^{-i\pi}|$...
Pongo $y = x^{2}$ quindi $y=\frac {x^{2}}{pongo}$
[tratto da un compito in classe di uno studente di prima superiore]
Il vero gnomone aureo: http://thumbs.dreamstime.com/z/gnomo-de ... 526933.jpg
Pongo $y = x^{2}$ quindi $y=\frac {x^{2}}{pongo}$
[tratto da un compito in classe di uno studente di prima superiore]
Il vero gnomone aureo: http://thumbs.dreamstime.com/z/gnomo-de ... 526933.jpg
Re: intersezione di circonferenze
Si Ivana, apriamo, apriamo....magari partirei dall'inizio con un "avviamento a geogebra".
Vedo intanto che Admin ha già provveduto ad aggiungere due nuovi pulsanti con le relative istruzioni.
Vedo intanto che Admin ha già provveduto ad aggiungere due nuovi pulsanti con le relative istruzioni.
_________________
$\text { }$ciao ciao
ciao
E' la somma che fa il totale (Totò)
$\text { }$ciao
E' la somma che fa il totale (Totò)
Re: intersezione di circonferenze
Supponiamo di voler calcolare per un cerchio l'area della mezza "mandorla" con un integrale: l'elemento di area è $dA\/=\/y\/dx$ confabtor ha scritto:io penna carta e penna alla mano avevo ottenuto una formula molto più complessa della tua (e probabilmente sbagliata)...
$\left\{\begin{array}{lC+30}x\/=\/r\/\cos{\vartheta} \\ y\/=\/r\/\sin{\vartheta} \end{array}\right.$
equazioni parametriche della circonferenza
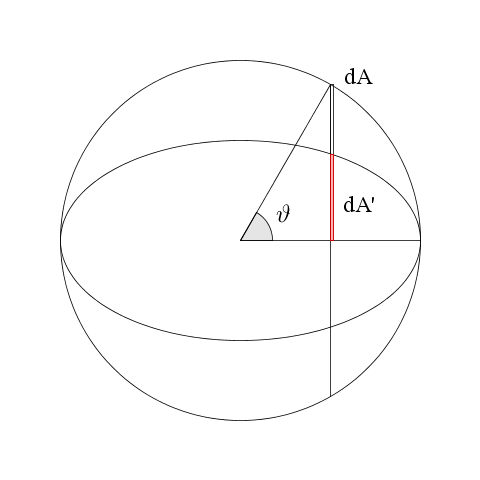
A tale elemento corrisponde per l'ellisse $dA'\/=\/y'\/dx$ con
$\left\{\begin{array}{lC+30}x\/=\/a\/\cos{\vartheta} \\ y'\/=\/b\/\sin{\vartheta} \end{array}\right.$
equazioni parametriche dell'ellisse e $a\/=\/r$.
Evidentemente i due integrali stanno in proporzione come $y'$ e $y$: $k\/=\/b/a$.
il panurgo
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
Re: intersezione di circonferenze
Il mio calcolo non teneva conto della circonferenza circoscritta, ma avevo proceduto come per il caso del cerchio considerando il triangolo e il segmento ellittico (tuttavia, ho dei dubbi sulla correttezza della formula ottenuta e non ho ancora avuto tempo di ricontrollarla con l'attezione che merita).
Ah, se i portieri avessero sulla maglia: $|e^{-i\pi}|$...
Pongo $y = x^{2}$ quindi $y=\frac {x^{2}}{pongo}$
[tratto da un compito in classe di uno studente di prima superiore]
Il vero gnomone aureo: http://thumbs.dreamstime.com/z/gnomo-de ... 526933.jpg
Pongo $y = x^{2}$ quindi $y=\frac {x^{2}}{pongo}$
[tratto da un compito in classe di uno studente di prima superiore]
Il vero gnomone aureo: http://thumbs.dreamstime.com/z/gnomo-de ... 526933.jpg




