I due recinti

[franco]

Un allevatore di cavalli vuole realizzare due recinti identici utilizzando $40$ pannelli metallici di $2$ metri di lunghezza.
Qual è la superficie massima di terreno delimitato da ciascun recinto?


ciao

Franco


www.diophante.fr
D.4942

Un éleveur de chevaux souhaite construire deux clôtures identiques avec 40 panneaux métalliques de 2 mètres de long.
Quelle est la surface maximale du terrain délimité par chaque clôture ?

[panurgo]

Se non mi sbaglio, circa $5\left(1+\sqrt{5} + \sqrt{5 + 2 \sqrt{5}}\right)$...

[franco]

Se non mi sbaglio, circa $5\left(1+\sqrt{5} + \sqrt{5 + 2 \sqrt{5}}\right)$...

Apperò!

[franco]

Se non mi sbaglio, circa $5\left(1+\sqrt{5} + \sqrt{5 + 2 \sqrt{5}}\right)$...

Non mi torna ... se non ho sbagliato i conti, la tua formula equivale a circa $31,6 m^2$.
Facendo due semplici recinti poligonali regolari a 20 lati, la superficie totale è di oltre $252 m^2$

[Maurizio59]

...
Non mi torna ... se non ho sbagliato i conti, la tua formula equivale a circa $31,6 m^2$.
Facendo due semplici recinti poligonali regolari a 20 lati, la superficie totale è di oltre $252 m^2$

Franco, hai ragione.
Panurgo ha considerato l'area di un solo recinto a forma di poligono regolare di 20 lati lunghi 1 metro (e non 2) mentre tu hai calcolato l'area totale dei due recinti con lati di 2 metri. Per questo il tuo risultato è circa otto volte quello di Panurgo.

[franco]

In effetti la domanda è relativa al singolo recinto...
Però c'è sicuramente modo di fare recinti molto più estesi rispetto a semplici 20-goni regolari.

[panurgo]

In effetti la domanda è relativa al singolo recinto...
Però c'è sicuramente modo di fare recinti molto più estesi rispetto a semplici 20-goni regolari.

1.il recinto deve essere un poligono convesso: rovesciando gli angoli concavi otteniamo un recinto più grande con lo stesso perimetro.
2.a parità di perimetro il cerchio è la figura con l'area maggiore
3.l'n-gono regolare è la migliore approssimazione di un cerchio...

Si può fare meglio solo se 2 è falsa.

P.S.: Mi scuso per aver confuso il 2 con l'1.

[franco]

Se dovessi fare un recinto con 20 pannelli, il poligono regolare a venti lati da $126 m^2$ circa sarebbe certamente la soluzione ottimale.

In questo caso però dobbiamo farle due recinti uguali con 40 pannelli.

Mettendone alcuni in comune, si riesce ad aumentare l'area di ogni recinto.
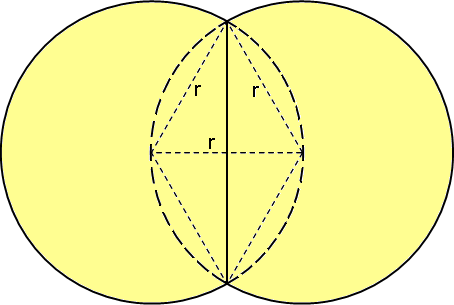
Per intenderci, disegnando archi di circonferenza anzichè poligoni, sarebbe una roba così:

due_recinti_1.png (21.75 KiB) Visto 1362 volte

Naturalmente, i pannelli in comune devono essere in numero pari in modo da poter dividere i restanti in maniera uguale per i due recinti.


Io ho impostato queste formule:

due_recinti_2.png (41.18 KiB) Visto 1362 volte

Non sono riuscito a risolverle analiticamente, ma lavorando per approssimazioni successive ho trovato che l'area massima si ottiene mettendo in comune 6 pannelli:

due_recinti_3.png (24.79 KiB) Visto 1362 volte

Circa $157 m^2$, naturalmente salvo errori ...

PS i disegni non sono in scala e anche il numero di lati è messo a caso ...

[Maurizio59]

Bel lavoro, Franco.

... disegnando archi di circonferenza anzichè poligoni ...

E' interessante notare che, in questo caso, l'area massima si ha quando la distanza tra i centri dei due cerchi è uguale al raggio dei cerchi come in figura.
.

L'area massima di un recinto diventa:
$$A=\frac{3L^2}{4(8\pi+3\sqrt3)}$$ Dove L è la lunghezza totale della recinzione. Nel caso L = 80 m l'area di un recinto diventa circa 158.265 m^2.

[franco]

Bel lavoro, Franco.

... disegnando archi di circonferenza anzichè poligoni ...

E' interessante notare ......

Avevo pensato di proporre la variante con 80 m di rete, ma l'hai già risolta

[newdelfo]

Non sono esperto di allevamenti equini, ma utilizzando due set di venti segmenti e ponendoli in modo da recintare una superficie minima (tendenzialmente nulla) , si ottengono contemporaneamente due recinti corrispondenti alla superficie terrestre (meno l' epsilon di cui sopra). Se non viene specificato che i due recinti devono essere separati, è una soluzione piuttosto laterale, ma...