Triangolo 5-7-8

[Quelo]

Triangolo578.png (49.19 KiB) Visto 7483 volte

Calcolare il lato del triangolo senza calcolatrice (scientifica)

[Bruno]

La prima cosa che mi è venuta in mente, Sergio, è questa identità, valida per un triangolo equilatero di lato l, con un punto interno di cui siano note le distanze dai tre vertici (qui la trascrivo sostituendo alle variabili i valori noti):
(5² + 7² + 8² + l²)² = 3·(5⁴ + 7⁴ + 8⁴ + l⁴).
Togliendo le parentesi, ottengo l'equazione:
(l² - 9)·(l² - 129) = 0,
il cui unico zero accettabile dà l = √129.

[Quelo]

Direi che non fa una piega e anche che non conoscevo l'identità

[Bruno]

Sergio, è riportata anche qui (e la fonte è il mitico Gardner), assieme ad altre formulette carine

[Maurizio59]

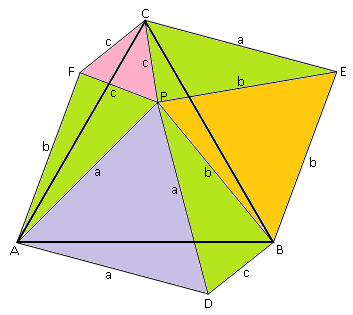
Per trovare l'area del triangolo equilatero si può usare anche la seguente formula:
$$A=\frac{\sqrt3}{8}(a^2+b^2+c^2)+\frac32S$$ dove S è l'area del triangolo di lati a,b,c.
Da questa formula si può dedurre una soluzione esclusivamente figurativa.
Eccola.

.
Notando che l'area dell'esagono irregolare ADBECF è il doppio di quella del triangolo equilatero ABC si ricava facilmente la formula indicata in precedenza.

[Maurizio59]

Riprendo questo vecchio problema per proporre una nuova variante.

All'interno di un triangolo rettangolo vi è un punto P le cui distanze dai tre vertici del triangolo sono 5, 7, 8.
- Trovare l'area del triangolo se esso è anche isoscele.
- Trovare l'area massima del triangolo.
- Generalizzare nel caso le distanze dai vertici siano a > b > c.

[Gianfranco]

Bel problema e belle le soluzioni di Bruno e Maurizio!
Riporto la citazione di Martin Gardner ricordata da Bruno.

Gardner_triangolo.png (85.29 KiB) Visto 2009 volte

Ho provato a ricavare la formula usando varianti della formula di Erone applicata ai 4 triangoli in gioco ma ho ottenuto formule equivalenti ma molto più complesse.
---
La citazione è tratta da:
Martin Gardner, Mathematical circus, 1968...1992, pag. 65.

[Gianfranco]

Cari amici, permettetemi un ragionamento immediato ed elementare che ho fatto appena ho visto la figura per trovare un valore approssimato del lato.

tria758.png (22.9 KiB) Visto 1934 volte

1) Dal triangolo a,7,5 ricavo che a<7+5; a<12.

2) Dal triangolo a,7,8, osservando che l'angolo col bollino è il meno ottuso dei tre angoli al centro, ricavo con Pitagora che $a>\sqrt{7^2+8^2}$; $a>10,63$

3) faccio la media dei due limiti e ottengo $a=11,32$

Il valore esatto invece è: $a=\sqrt{129}=11,3578...$