Dissezione della mitra in quadrato di 4 pezzi
Moderatori: Gianfranco, Bruno
Questo forum è una sezione del PORTALE DI BASE CINQUE
-
Gianfranco
- Supervisore del sito

- Messaggi: 1828
- Iscritto il: ven mag 20, 2005 9:51 pm
- Località: Sestri Levante
- Contatta:
Dissezione della mitra in quadrato di 4 pezzi
Cari amici, forse sto postando troppe cose sul Forum, ma questa notizia merita.
---
Vesa Timonen ha pubblicato su GitHub una dissezione della mitra in 4 pezzi.
Le dissezioni precedenti più note erano quelle di Samuel Loyd e Henry Dudeney.
- La dissezione di Samuel Loyd in 4 pezzi, purtroppo sbagliata perché la seconda figura non è un quadrato (1901).
- La dissezione di Henry Dudeney in 5 pezzi (1911).
- La dissezione di Vesa Timonen in 4 pezzi (2024).
Vedi figura.
Domande.
1) La dissezione di Loyd è davvero errata? Dov'é l'errore?
2) La dissezione di Loyd si può modificare leggermente in modo da renderla esatta?
3) Si può migliorare in qualche modo la dissezione di Vesa Timonen?
---
Vesa Timonen ha pubblicato su GitHub una dissezione della mitra in 4 pezzi.
Le dissezioni precedenti più note erano quelle di Samuel Loyd e Henry Dudeney.
- La dissezione di Samuel Loyd in 4 pezzi, purtroppo sbagliata perché la seconda figura non è un quadrato (1901).
- La dissezione di Henry Dudeney in 5 pezzi (1911).
- La dissezione di Vesa Timonen in 4 pezzi (2024).
Vedi figura.
Domande.
1) La dissezione di Loyd è davvero errata? Dov'é l'errore?
2) La dissezione di Loyd si può modificare leggermente in modo da renderla esatta?
3) Si può migliorare in qualche modo la dissezione di Vesa Timonen?
Pace e bene a tutti.
Gianfranco
Gianfranco
-
Maurizio59
- Livello 4

- Messaggi: 155
- Iscritto il: mar lug 26, 2022 9:02 am
Re: Dissezione della mitra in quadrato di 4 pezzi
Risposta 1.Gianfranco ha scritto: ↑gio mag 30, 2024 4:39 pm...
Domande.
1) La dissezione di Loyd è davvero errata? Dov'é l'errore?
2) La dissezione di Loyd si può modificare leggermente in modo da renderla esatta?
3) Si può migliorare in qualche modo la dissezione di Vesa Timonen?
La dissezione di Loyd è sbagliata in quanto con essa non si ottiene un quadrato ma un rettangolo.
Poniamo per semplicità a = 1.
Dopo il taglio delle due "punte" della mitra si ottiene un rettangolo le cui dimensioni sono 3/4 e 1.
Esso viene diviso in 6x7 = 42 rettangoli uguali divisi in due parti uguali attraverso una linea "a gradini" come in figura.
Le dimensioni di ogni rettangolino sono x = 1/7 e y = (3/4)x(1/6) = 1/8.
Le dimensioni del rettangolo ottenuto attraverso la traslazione delle due parti sono: base = 6x = 6/7 e altezza = 7y = 7/8.
Risposta 2. No.
Questo comporta che non tutti i rettangoli si possono trasformare in quadrati con questo metodo.
Quali caratteristiche deve avere un rettangolo in modo che si possa trasformare in un quadrato con il metodo dei "gradini"
Risposta 3. Scommetterei di no.
Re: Dissezione della mitra in quadrato di 4 pezzi
Partiamo dal quadrato.Maurizio59 ha scritto: ↑gio mag 30, 2024 10:50 pm...
Quali caratteristiche deve avere un rettangolo in modo che si possa trasformare in un quadrato con il metodo dei "gradini"
...
Nel tagliare i gradini abbiamo sempre un taglio orizzontale in più rispetto ai tagli verticali (o viceversa, vista la simmetria del quadrato): per ogni taglio orizzontale otteniamo una pedata della scala mentre le alzate sono due in più rispetto ai tagli verticali (uno perché il primo taglio comincia dal lato del quadrato e due perché si ottengono due scale)
Come da figura, $1$ taglio orizzontale e $0$ verticali forniscono $1$ pedata e $2$ alzate; $2$ tagli orizzontal1 e $1$ verticale forniscono $2$ pedate e $3$ alzate; $3$ tagli orizzontali e $2$ tagli verticali forniscono $3$ pedate e $4$ alzate. E così via.
Con $n$ pedate: la pedata sarà di $l/n$ e l'alzata sarà di $l/(n+1)$; la base del rettangolo sarà di $n+1$ pedate e la sua altezza sarà di $n$ alzate
$\begin{array}{lC}\displaystyle b=\frac{n+1}{n}l \\ \displaystyle h=\frac{n}{n+1}l\end{array}$
Possono essere trasformati in quadrati con il metodo dei gradini tutti i rettangoli il cui rapporto tra altezza e base è
$\displaystyle \frac{h}{b}=\left(\frac{n}{n+1}\right)^2$
dove $n$ è il numero dei gradini: un'infinità numerabile.
Nel caso della mitra, il rettangolo di Samuel Loyd ha
$\displaystyle \frac{h}{b}=\frac34$
quindi non il quadrato del rapporto di due interi consecutivi.
il panurgo
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
-
Gianfranco
- Supervisore del sito

- Messaggi: 1828
- Iscritto il: ven mag 20, 2005 9:51 pm
- Località: Sestri Levante
- Contatta:
Re: Dissezione della mitra in quadrato di 4 pezzi
Grazie Maurizio59 e Panurgo, ottime risposte, e velocissime!
Ora mi chiedo: possibile che Samuel Loyd abbia fatto questo errore?
Da indagare...
Pace e bene a tutti.
Gianfranco
Gianfranco
-
Gianfranco
- Supervisore del sito

- Messaggi: 1828
- Iscritto il: ven mag 20, 2005 9:51 pm
- Località: Sestri Levante
- Contatta:
Re: Dissezione della mitra in quadrato di 4 pezzi
Ho dato un'occhiata alla costruzione di Sam Loyd e mi sembra molto astuta, sia pur sbagliata (ammesso che la sua mitra sia ricavata da un quadrato)
La differenza fra i due lati del rettangolo finale è solo 1/56 a, meno del 2% (se non sbaglio)
Forse Sam ne era consapevole ci ha comunque provato?
Forse Sam ne era consapevole ci ha comunque provato?
Pace e bene a tutti.
Gianfranco
Gianfranco
Re: Dissezione della mitra in quadrato di 4 pezzi
Lo ritengo probabile vista la passione di Loyd per per questo tipo di puzzleGianfranco ha scritto: ↑ven mag 31, 2024 5:03 pm[...]
Forse Sam ne era consapevole ci ha comunque provato?
il panurgo
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
-
Gianfranco
- Supervisore del sito

- Messaggi: 1828
- Iscritto il: ven mag 20, 2005 9:51 pm
- Località: Sestri Levante
- Contatta:
Re: Dissezione della mitra in quadrato di 4 pezzi
Bella la versione interattiva! Grazie per la segnalazione.
Pace e bene a tutti.
Gianfranco
Gianfranco
-
Maurizio59
- Livello 4

- Messaggi: 155
- Iscritto il: mar lug 26, 2022 9:02 am
-
Gianfranco
- Supervisore del sito

- Messaggi: 1828
- Iscritto il: ven mag 20, 2005 9:51 pm
- Località: Sestri Levante
- Contatta:
Re: Dissezione della mitra in quadrato di 4 pezzi
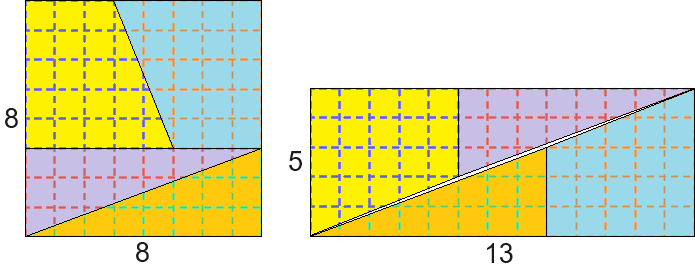
Anche questa dissezione è un indizio...Maurizio59 ha scritto: ↑lun giu 03, 2024 3:32 pmAltra dissezione ingannevole attribuita a Loyd (o a suo fratello?) è quella in figura.
Samuel Loyd aveva 8 fratelli/sorelle ma non sapevo che anche uno di essi inventasse puzzles matematici. Qual è la fonte della tua ipotesi/domanda?
Pace e bene a tutti.
Gianfranco
Gianfranco
-
Maurizio59
- Livello 4

- Messaggi: 155
- Iscritto il: mar lug 26, 2022 9:02 am
Re: Dissezione della mitra in quadrato di 4 pezzi
Una completa e dettagliata descrizione in inglese si trova qui:
https://en.wikipedia.org/wiki/Chessboard_paradox
https://en.wikipedia.org/wiki/Chessboard_paradox
-
Gianfranco
- Supervisore del sito

- Messaggi: 1828
- Iscritto il: ven mag 20, 2005 9:51 pm
- Località: Sestri Levante
- Contatta:
Re: Dissezione della mitra in quadrato di 4 pezzi
Grazie Maurizio59, un bell'articolo di Wikipedia.
Pace e bene a tutti.
Gianfranco
Gianfranco