La città triangolare di Alcuino da York

[Gianfranco]

Cari amici, ultimamente abbiamo raggiunto risultati davvero buoni, secondo me straordinari, in problemi di "packing".
Perciò oso proporvi un problema, antico ma ancora aperto, di Alcuino da York che per me è rimasto in sospeso.
---
XXVIII. PROPOSIZIONE SU UNA CITTA' TRIANGOLARE.
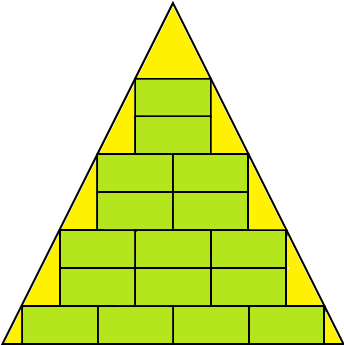
C'è una città triangolare che su un lato misura 100 piedi, sull'altro lato 100 piedi e sulla base 90 piedi.
Voglio costruirvi delle case, in modo che ogni casa sia lunga 20 piedi e larga 10.
Dica, chi può, quante case può contenere la città?
---
Una soluzione è 16 ed è rappresentata nella figura seguente.

Alcuin_triangula.png (20.33 KiB) Visto 28369 volte

Il problema è: si può migliorare?
Oppure dimostrare che 16 è il massimo?
Oppure trovare un'altra soluzione equivalente ma più carina?

[Maurizio59]

Alcune riflessioni Alcuine.
Quando vidi per la prima volta questo problema mi colpì la particolarità delle forme e le loro dimensioni.
Mi chiesi subito quale fosse l'idea dietro ad una simile scelta.
Consideriamo il fatto che intuitivamente si tende ad accostare i rettangoli disponendoli a contatto con la base del triangolo e poi ad impilarli.
Supponiamo che Alcuino volesse evitare soluzioni troppo semplici come quella in figura, dove l'altezza H del triangolo è uguale alla base B.

Con Pitagora si può trovare il lato obliquo del triangolo. Esso è $L = \frac{\sqrt5}{2}B = 1.118...B$
Questa disposizione può essere evitata se imponiamo la condizione L < 1.118...B.
Scegliendo i valori L = 10 (o 100) e B = 9 (o 90) otteniamo un valore molto vicino (L = 1.1111...B) in modo che non sia facile visivamente individuare l'errore.
Questo implica che ogni soluzione non può avere 4 rettangoli disposti a contatto con la base lungo il loro lato di lunghezza 2 (o 20).

[Gianfranco]

Grazie Maurizio59 e bella la soluzione QUASI giusta!
---
Questa è la soluzione di Alcuino.

I due lati della città uniti misurano 200 piedi; la metà di 200 è 100. Ma poiché la base misura 90 piedi, la metà di 90 è 45. E poiché la lunghezza di ogni casa è di 20 piedi, mentre la larghezza è di 10, dividi 100 per 20, ottenendo 5. La decima parte di 40 è 4, allora moltiplica 5 per 4, ottenendo 20. In questo modo la città può contenere 20 case.

Secondo me, a una prima interpretazione, Alcuino propone una semplice divisione di aree senza tentare di fare "impaccamenti".
E approssima, direi abbastanza bene, l'area del triangolo a quella di un rettangolo formato da 5*4=20 case. Ma evita di usare il teorema di Pitagora, che conosceva certamente.

AlcuinTriangolo.png (29.27 KiB) Visto 28142 volte

---
Su Alcuino e su Beda ho alcune idee fantascientifiche che forse prima o poi dirò.
Nascono dalla considerazione che nei loro scritti compaiono improvvisamente per la prima volta nella storia certi problemi matematici incredibilmente attuali oggi.
Però loro danno delle soluzioni (volutamente?) ingenue o con qualche errore.
Cosa sapevano veramente?
Da chi hanno ricevuto questi problemi?
Mi fermo qui.

[Gianfranco]

Quando vidi per la prima volta questo problema mi colpì la particolarità delle forme e le loro dimensioni.
Mi chiesi subito quale fosse l'idea dietro ad una simile scelta.

acuin_tri.png (8.66 KiB) Visto 22396 volte

La tua soluzione quasi-esatta conferma le mie ipotesi fantastiche.
1) Questo problema, considerato come un problema di "impacchettamento" è sottilmente difficile: si presta a una soluzione intuitiva che però non è proprio esatta. Trovare una soluzione esatta è molto difficile.
2) Alcuino propone una soluzione pseudo-ingegnosa, ma ingenua e comunque sbagliata e inverosimile. Perché? Cosa sapeva davvero?
3) Ai tempi di Alcuino non esistevano i problemi di "impaccamento" e solo oggi, dopo più di 1000 anni questo è diventato davvero un problema "Ad acuendos juvenes".
Conclusione fantastica: Alcuino ha ricevuto questi problemi da extraterrestri che in momenti opportuni visitano il nostro pianeta e lasciano spunti per far migliorare l'umanità.
Ma ma ci lasciano liberi di capire oppure no. Un po' come dire: "Chi ha orecchie per intendere, intenda."

[Gianfranco]

Quando vidi per la prima volta questo problema mi colpì la particolarità delle forme e le loro dimensioni.
Mi chiesi subito quale fosse l'idea dietro ad una simile scelta.

acuin_tri.png (8.66 KiB) Visto 22396 volte

La tua soluzione quasi-esatta conferma le mie ipotesi fantastiche.
1) Questo problema, considerato come un problema di "impacchettamento" è sottilmente difficile: si presta a una soluzione intuitiva che però non è proprio esatta. Trovare una soluzione esatta è molto difficile.
2) Alcuino propone una soluzione pseudo-ingegnosa, ma ingenua e comunque sbagliata e inverosimile. Perché? Cosa sapeva davvero?
3) Ai tempi di Alcuino non esistevano i problemi di "impaccamento" e solo oggi, dopo più di 1000 anni questo è diventato davvero un problema "Ad acuendos juvenes".
Conclusione fantastica: Alcuino ha ricevuto questi problemi da extraterrestri che in momenti opportuni visitano il nostro pianeta e lasciano spunti per far migliorare l'umanità.
Ma ma ci lasciano liberi di capire oppure no. Un po' come dire: "Chi ha orecchie per intendere, intenda."