Una tavola di cioccolato.

[Bruno]

Ancora un problema dell'ingegner Carmelo Giugno

B5 - Testo.jpg (24.42 KiB) Visto 26270 volte

B5 - Rettangoli di cioccolato.jpg (20.88 KiB) Visto 26270 volte

---
Senza WolframAlpha

[franco]

Non ho usato WolframAlpha ma un aiutino con Excel me lo sono preso ...

$a4=x$
$a6=a5$ e poi risolvo rispetto a $x$:

$a1/48=36/x$ --> $a1=1728/x$
$(a5-18)/48=(a5+18)/x$ --> $a5=18(x+48)/(x-48)$

A questo punto posso calcolare con excel la somma di tutti i pezzi ipotizzando diversi valori di $x>48$

Con pochissimi tentativi si arriva al valore corretto che consente poi di ricavare le dimensioni degli altri pezzi.

Non la riporto per lasciare il piacere a solutori più abili che magari trovano una strada che non necessita nemmeno di excel

ciao

[Quelo]

Il rettangolo 18q può essere solo 1x18, 2x9 o 3x6
Prendiamo quello nel mezzo: 2x9
Le aree $a_5$ e $a_6$ avranno base $x$ e altezza 9
le aree $a_1$ e $a_3$ avranno base $x-2$, mentre le aree $a_2$ e $a_4$ avranno base $x+2$
Quindi $x-2$ è divisore di $48$, mentre $x+2$ è divisore di $36$
L'unica soluzione è $x=10$ da cui si rcava facilmente:
$a_1=24$
$a_4=72$
$a_5=a_6=90$
$\sum_{j=1}^6{a_j}=360$

[Bruno]

Prendiamo quello nel mezzo: 2x9

E i casi primo e terzo, Sergio?
Immagino che per te sia evidente, ma per chi ci legge forse è meglio chiarire

[Bruno]

Non ho usato WolframAlpha ma un aiutino con Excel me lo sono preso ...

[franco]

Prendiamo quello nel mezzo: 2x9

E i casi primo e terzo, Sergio?
Immagino che per te sia evidente, ma per chi ci legge forse è meglio chiarire

In realtà ci sono anche i casi 6x3, 9x2 e 18x1 ... o no?

(poi è evidente che la soluzione trovata è l'unica che funziona )

[Bruno]

Direi di sì, Franco: penso che Sergio abbia voluto proporre una sintesi di una sintesi...

[Quelo]

Ieri sera andavo un po' di fretta.
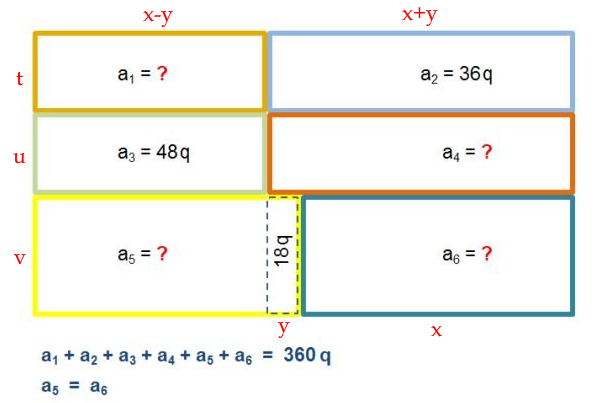
Indichiamo con $x$ la base di $a_5$, $a_6$, con $y$ la base di $18q$ e con $t$, $u$, $v$ le altezze

cioccolato.png (91.86 KiB) Visto 26213 volte

Avremo $\displaystyle t=\frac{36}{x+y}$, $\displaystyle u=\frac{48}{x-y}$, $\displaystyle v=\frac{18}{y}$

$y$ può assumere i valori 1, 2, 3, 6, 9, 18
$x+y$ è divisore di 36, $x-y$ è divisore di 48, la differenza tra i due è $2y$
Quindi scelto $y$ devo selezionare le coppie di divisori che distano $2y$, emergono 9 casi, che possono essere verificati con pochi semplici calcoli

Possiamo tuttavia considerare che $2x(t+u+v)=360$ e con qualche passaggio algebrico ricaviamo:

$3x^3-16x^2y-xy^2+30y^3=0$ da cui sostituendo $x$ con $ay$ ricavo un'equazione di terzo grado con una sola soluzione reale tale per cui $x=5y$

I casi y = 6, 9, 18 non hanno soluzione, mentre per y = 1, 2, 3, quale che sia la scelta di y si ha sempre:

$\displaystyle a_1=\frac{36(x-y)}{x+y}=24$
$\displaystyle a_4=\frac{48(x+y)}{x-y}=72$
$\displaystyle a_5=a_6=\frac{18x}{y}=90$

[panurgo]

Come dici tu, $x=5y$. Segue

$\left\{\begin{array}{lC}
\displaystyle t=\frac{36}{x+y}=\frac{6}{y} \\
\displaystyle u=\frac{48}{x-y}=\frac{12}{y}=2t \\
\displaystyle v=\frac{18}{y}=3t
\end{array}\right.$

quindi $y$ può assumere i valori $1$, $2$, $3$ e $6$.

QuattroTavoleDiCioccolata.01.png (15.27 KiB) Visto 26154 volte

[Quelo]

Sì, anche il 6, avevo sbagliato un conto

[Bruno]

Ottimo