Riempire una griglia

[Tino]

Premetto che questo gioco è conosciuto quindi potrebbe trovarsi in rete con molte informazioni, ma siccome non so come si chiama (voi lo sapete?) non ho appigli per cercare.

Abbiamo una griglia 10 per 10. Il gioco consiste nel riempire tale griglia coi numeri da 1 a 100 consecutivamente, dove la regola per passare da una casella alla successiva è illustrata dalla seguente immagine (la casella di partenza è quella segnata in rosso, le altre caselle segnate sono le possibili destinazioni).



Per esempio uno potrebbe cominciare così:



Per trovare una soluzione può essere utile risolvere una griglia 5x5.

Diciamo che due caselle A e B sono "collegate" se esiste una soluzione che parte in A e finisce in B.
Fissata una casella A, quali sono le caselle collegate ad A? Per esempio quali sono le caselle collegate a quella in alto a sinistra?

Per quali n una griglia nxn ha soluzione?

Sono domande a cui ancora non so rispondere.

[Daniela]

Ci ho giocato un sacco durante le lezioni noiose a scuola. Esistono soluzioni per il 10x10 ma non sono proprio facilissime da trovare, se si gioca con carta e penna.

[fabtor]

Me lo ricordo anch'io ai tempi tutta la classe ci giocava durante le ore di italiano , ricordo che una volta un mio compagno aveva trovato una soluzione e aveva ritagliato il quadrato e lo aveva incollato sul diario... altre volte altri compagni erano riusciti ad arrivare a 97 / 98 ... Tuttavia l'unica cosa che so è che il 10x10 ha almeno una soluzione (quella del mio compagno che tutta la classe aveva più volte ricontrollato ) ... è proprio vero che volendo si trova da far matematica dietro ogni angolo.

[Pasquale]

Alla prima domanda non rispondo, perché non mi riesce di farlo.
Rispetto alla seconda, posso dire che per tutti gli n fra 5 e 10 esiste sempre una soluzione, anzi, data una soluzione, ne troviamo subito altre, derivate da simmetrie e rotazioni.

Ad esempio, data la soluzione:



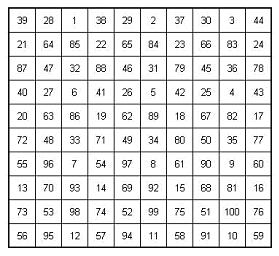
una derivata può essere la seguente:



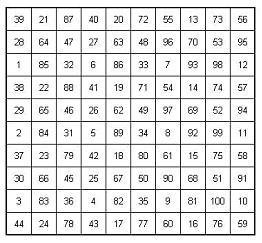
ed osservando bene, se ne trovano in tutto ben 8, praticamente uguali.

Più difficile, come già detto, è trovare tutte le soluzioni possibili, data la casella di partenza.
Non sono nemmeno sicuro che una qualsiasi casella iniziale porti sempre a soluzione, anzi direi di no.
Segue un esempio di una diversa soluzione rispetto alla stessa casella di partenza della prima griglia, che riporto nuovamente per il confronto:




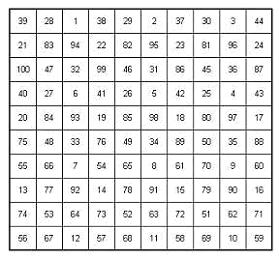
Per la casella iniziale, considerate le rotazioni e simmetrie, è sufficiente cercare nella prima metà del quadrato 5x5 in alto a sinistra, comprendente 15 caselle (cioè una sola delle 2 parti in cui il quadrato viene diviso dalla diagonale che parte dall'angolo in alto a sinistra)

Riporto, infine un esempio di soluzione per le griglie 9x9, 8x8, 7x7, 6x6, 5x5, a dimostrazione di quanto affermato prima relativamente alla seconda domanda posta:


25 70 49 26 71 50 27 72 51
65 01 36 66 02 37 67 03 38
48 29 12 47 28 13 46 33 14
24 69 54 23 68 53 22 73 52
64 06 35 77 05 34 60 04 39
43 30 11 44 31 10 45 32 15
19 76 55 20 75 78 21 74 59
63 07 42 62 08 41 61 09 40
56 81 18 57 80 17 58 79 16

55 37 01 56 38 02 57 39
09 22 53 10 23 52 11 24
31 49 19 32 48 18 33 47
54 36 04 51 35 03 58 40
08 21 62 07 20 42 12 25
30 50 16 29 45 17 34 46
61 64 05 60 63 06 59 41
15 28 44 14 27 43 13 26

01 20 17 02 45 16 03
27 12 39 26 13 38 25
18 32 44 19 35 43 46
06 21 14 05 40 15 04
28 11 36 31 10 37 24
49 33 41 48 34 42 47
07 22 29 08 23 30 09

01 21 26 02 20 31
28 36 18 29 35 17
25 11 08 32 14 07
04 22 27 03 19 30
09 33 15 10 34 16
24 12 05 23 13 06

01 25 18 02 24
20 10 05 21 11
07 16 13 08 17
04 22 19 03 23
14 09 06 15 12

[giobimbo]

Sembra che sia conosciuto come "Gioco del 100".
Il professor Favero ne fa una analisi interessante nel sito della Vialattea.net.

[Tino]

Grazie, ma l'unico gioco del 100 che ho trovato e' questo. Potresti fornire un rimando ("link")?

[giobimbo]

Tino, quello che hai trovato è il "gioco del cento"...

La pagina del professor Favero è questa:
http://www.vialattea.net/esperti/php/ri ... p?num=2288" target="_blank
e al suo interno contiene un link ad un'altra pagina dove descrive la sua strategia risolutiva.

[Tino]

Tino, quello che hai trovato è il "gioco del cento"...

Non capisco, non è quello che avevi detto tu? Gioco del cento, no?

Grazie comunque

[Pasquale]

E' tutto chiaro: esistono 2 giochi del 100...totale 200.

[Daniela]

cari amici sono appena venuta a sapere che questo gioco si chiama, in inglese, "Euler's knight". (knight=cavaliere= il cavallo degli scacchi). Buon googling e buon divertimento