Cari amici,
Ecco il problema n. dello Scottish Book.
Chi ha un po' di tempo per tradurlo in italiano?
Grazie, buone vacanze e buon lavoro.
Gianfranco
Scottish Book n.147
Moderatori: Gianfranco, Bruno
Questo forum è una sezione del PORTALE DI BASE CINQUE
-
Gianfranco
- Supervisore del sito
- Messaggi: 1828
- Iscritto il: ven mag 20, 2005 9:51 pm
- Località: Sestri Levante
- Contatta:
Scottish Book n.147
- Allegati
-
- Scottish Book n.147
- prob147.gif (7.22 KiB) Visto 9703 volte
Pace e bene a tutti.
Gianfranco
Gianfranco
Re: Scottish Book n.147
Ciao a tutti,
ho appena terminato una settimana di vacanze e vedo con piacere che il forum si è animato di una serie di problemi Scozzesi piuttosto intriganti; in particolare mi piace questo del biliardo (che mi porta alla mente il mio esordio nel forum):
Supponiamo che una palla da biliardo venga lanciata con un angolo di 45° a partire da un angolo di un biliardo rettangolare e i cui lati hanno un rapporto razionale. Dopo un numero finito di rimbalzi sulle sponde, finirà in uno dei tre altri angoli?
ciao
ho appena terminato una settimana di vacanze e vedo con piacere che il forum si è animato di una serie di problemi Scozzesi piuttosto intriganti; in particolare mi piace questo del biliardo (che mi porta alla mente il mio esordio nel forum):
Supponiamo che una palla da biliardo venga lanciata con un angolo di 45° a partire da un angolo di un biliardo rettangolare e i cui lati hanno un rapporto razionale. Dopo un numero finito di rimbalzi sulle sponde, finirà in uno dei tre altri angoli?
ciao
Ultima modifica di franco il lun ago 04, 2008 6:10 pm, modificato 1 volta in totale.
Franco
ENGINEER
noun. (en-juh-neer)
someone who does precision guesswork based on unreliable data provided by those of questionable knowledge.
See also wizard, magician
ENGINEER
noun. (en-juh-neer)
someone who does precision guesswork based on unreliable data provided by those of questionable knowledge.
See also wizard, magician
Re: Scottish Book n.147
La soluzione di questo ce l'ho. Mi serve solo il tempo di metterla in bella...Gianfranco ha scritto:Forse, con queste proposte tratte dallo Scottish Book o esagerato!
il panurgo
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
-
Gianfranco
- Supervisore del sito
- Messaggi: 1828
- Iscritto il: ven mag 20, 2005 9:51 pm
- Località: Sestri Levante
- Contatta:
Re: Scottish Book n.147
Grazie Franco per la traduzione e grazie Panurgo per l'impegno a risolverlo.
OOOps, mi sono accorto di aver dimantica l'h davanti all'o.
Ero troppo stanco...
Gianfranco
OOOps, mi sono accorto di aver dimantica l'h davanti all'o.
Ero troppo stanco...
Gianfranco
Pace e bene a tutti.
Gianfranco
Gianfranco
Re: Scottish Book n.147
E' l'unico che (forse) è alla mia portata.
Avevo pensato di dimostrarlo graficamente con l'ausilio di questo disegno:
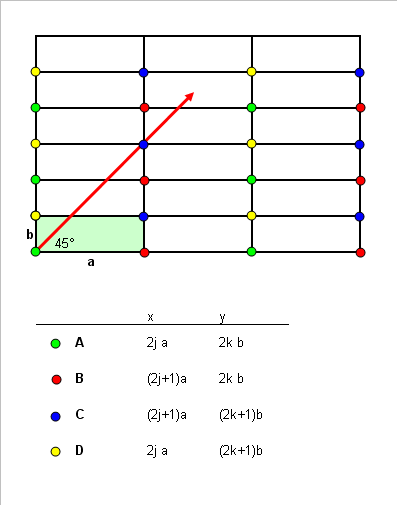
Se i lati sono in rapporto razionale a/b (con a>b) la biglia finisce in una buca rimbalzando a-1 volte sulla sponda lunga e b-1 volte sulla corta.
Se a e b sono entrambi dispari la biglia finirà nella buca C (blu)
Se a è dispari e b pari finirà nella buca B (rossa)
Se a è pari e b dispari finirà nella buca D (gialla)
N.B. Naturalmente è impossibile che la biglia torni alla buca A (verde) di partenza!
(salvo errori)
ciao
Avevo pensato di dimostrarlo graficamente con l'ausilio di questo disegno:
Se i lati sono in rapporto razionale a/b (con a>b) la biglia finisce in una buca rimbalzando a-1 volte sulla sponda lunga e b-1 volte sulla corta.
Se a e b sono entrambi dispari la biglia finirà nella buca C (blu)
Se a è dispari e b pari finirà nella buca B (rossa)
Se a è pari e b dispari finirà nella buca D (gialla)
N.B. Naturalmente è impossibile che la biglia torni alla buca A (verde) di partenza!
(salvo errori)
ciao
Franco
ENGINEER
noun. (en-juh-neer)
someone who does precision guesswork based on unreliable data provided by those of questionable knowledge.
See also wizard, magician
ENGINEER
noun. (en-juh-neer)
someone who does precision guesswork based on unreliable data provided by those of questionable knowledge.
See also wizard, magician
Re: Scottish Book n.147
Il problema consiste proprio nel dimostrare che questa affermazione è sempre vera e il tuo disegno non riesce a convicermi di ciò! Forse, se ti spieghi meglio...franco ha scritto:
Se i lati sono in rapporto razionale a/b (con a>b) la biglia finisce in una buca rimbalzando a-1 volte sulla sponda lunga e b-1 volte sulla corta.
il panurgo
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
Re: Scottish Book n.147
Hai ragione, non mi sono tanto spiegato e provo allora ad esporre più chiaramente il mio ragionamento.
Intanto se il rapporto fra i due lati è un razionale a/b posso utilizzare un'opportuna unità di misura tale per cui i lati del biliardo misurino appunto a e b.
(Il fatto che nel precedente post avessi indicato a>b serviva solo ad identificare le due sponde come lunga e corta ma in realtà è assolutamente irrilevante).
Le coordinate delle "famiglie" delle 4 buche A, B, C e D, ottenute per riflessioni successive del biliardo rispetto alle sponde sono quelle che avevo indicato nella figura:
A: x=2ja ; y=2kb
B: x=(2j+1)a ; y=2kb
C: x=(2j+1)a ; y=(2k+1)b
D: x=2ja ; y=(2k+1)b
con j e k interi.
La traiettoria della biglia (a 45° partendo dall'origine) è rappresentata dalla retta y=x.
Se sia a che b sono dispari allora esistono sicuramente una coppia di j e k tali che risulti (2j+1)a=(2k+1)b in particolare i valori minimi saranno j=(b-1)/2 e k=(a-1)/2. La biglia finirà nella buca C.
Se a è pari e b dispari allora esistono sicuramente una coppia di j e k tali che risulti (2j+1)a=2kb in particolare i valori minimi saranno j=(b-1)/2 e k=a/2. La biglia finirà nella buca B.
Se a è dispari e b pari allora esistono sicuramente una coppia di j e k tali che risulti 2ja=(2k+1)b in particolare i valori minimi saranno j=b/2 e k=(a-1)/2. La biglia finirà nella buca D.
Spero risulti più chiaro, del resto oggi i 45° più che all'inclinazione della traiettoria somigliano alla temperatura esterna ed è già tanto che non mi sia collassato!
ciao
Intanto se il rapporto fra i due lati è un razionale a/b posso utilizzare un'opportuna unità di misura tale per cui i lati del biliardo misurino appunto a e b.
(Il fatto che nel precedente post avessi indicato a>b serviva solo ad identificare le due sponde come lunga e corta ma in realtà è assolutamente irrilevante).
Le coordinate delle "famiglie" delle 4 buche A, B, C e D, ottenute per riflessioni successive del biliardo rispetto alle sponde sono quelle che avevo indicato nella figura:
A: x=2ja ; y=2kb
B: x=(2j+1)a ; y=2kb
C: x=(2j+1)a ; y=(2k+1)b
D: x=2ja ; y=(2k+1)b
con j e k interi.
La traiettoria della biglia (a 45° partendo dall'origine) è rappresentata dalla retta y=x.
Se sia a che b sono dispari allora esistono sicuramente una coppia di j e k tali che risulti (2j+1)a=(2k+1)b in particolare i valori minimi saranno j=(b-1)/2 e k=(a-1)/2. La biglia finirà nella buca C.
Se a è pari e b dispari allora esistono sicuramente una coppia di j e k tali che risulti (2j+1)a=2kb in particolare i valori minimi saranno j=(b-1)/2 e k=a/2. La biglia finirà nella buca B.
Se a è dispari e b pari allora esistono sicuramente una coppia di j e k tali che risulti 2ja=(2k+1)b in particolare i valori minimi saranno j=b/2 e k=(a-1)/2. La biglia finirà nella buca D.
Spero risulti più chiaro, del resto oggi i 45° più che all'inclinazione della traiettoria somigliano alla temperatura esterna ed è già tanto che non mi sia collassato!
ciao
Franco
ENGINEER
noun. (en-juh-neer)
someone who does precision guesswork based on unreliable data provided by those of questionable knowledge.
See also wizard, magician
ENGINEER
noun. (en-juh-neer)
someone who does precision guesswork based on unreliable data provided by those of questionable knowledge.
See also wizard, magician
Re: Scottish Book n.147
Scusa Franco, ma (sarà questo gelo polare che mi paralizza il cervello? ) mi c'è voluto un po' per capire: ecco, invece, il mio pacco.
Consideriamo un tavolo da carambola (così evitiamo di discutere sulle dimensioni delle buche ecc.) di lati $a$ e $b$ con $a \/ < \/ b$: con questa assunzione non si ha perdita di generalità perché lo scambio di $a$ con $b$
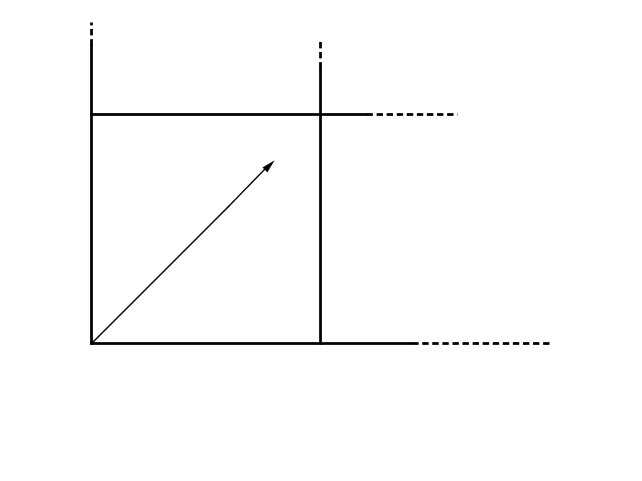
equivale a iniziare il moto della palla dall'altro angolo adiacente al lato corto
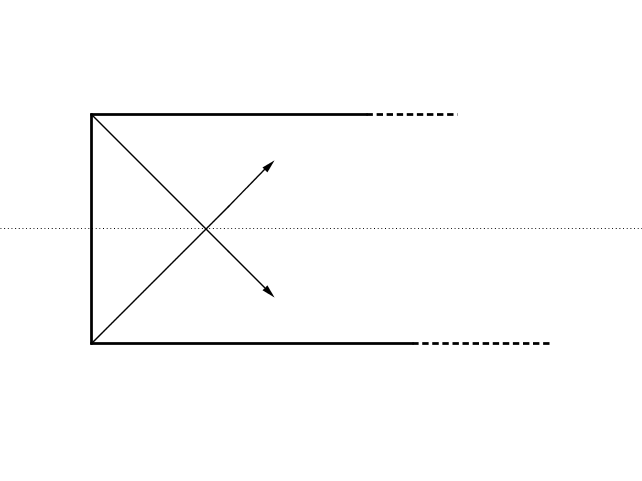
e il piano del biliardo possiede un piano di simmetria perpendicolare passante per l'asse dei lati corti che rende equivalenti le due situazioni.
Prendiamo due numeri interi, $m$ e $n$ tali che $m/n \/ = \/ a/b$ con $m/n$ frazione ridotta i minimi termini, come misure del piano del biliardo.
Dato che il moto è a 45°, la palla percorre distanze eguali longitudinalmente e trasversalmente e al primo rimbalzo colpisce la sponda del lato lungo ad una distanza $m$ dal lato corto
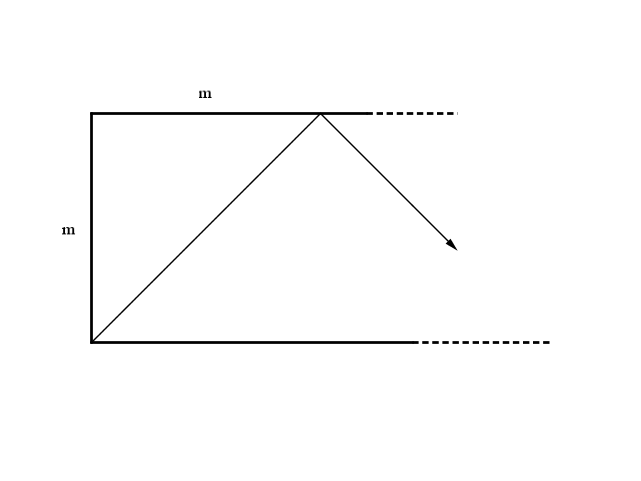
Al secondo ribalzo la palla colpisce la sponda opposta ad una distanza di $2m$, al terzo, di $3m$, e così via fino a che la distanza del rimbalzo dal lato corto successivo non sarà $r \/ < \/ m$
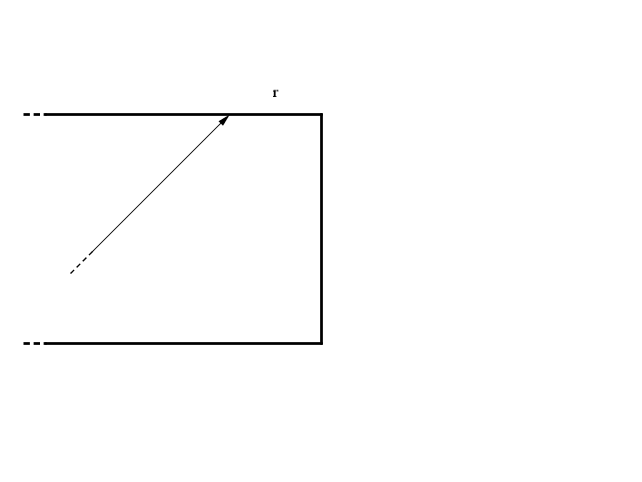
La palla esegue, col suo moto, una divisione col resto: $n \/ = q \/ \times \/ m \/ + \/ r$.
A questo punto la palla rimbalza prima sul lato corto e poi sul lato lungo, procedendo in verso opposto.
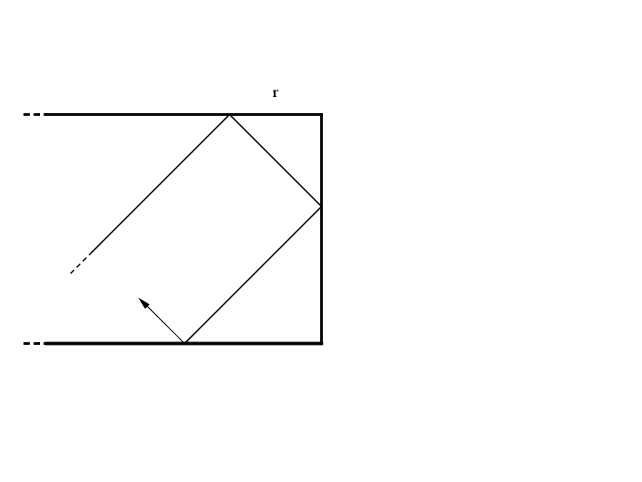
Ma, se noi poniamo al posto della sponda uno specchio (elastico!) vedremo l'immagine riflessa della palla che prosegue la sua corsa sul biliardo speculare
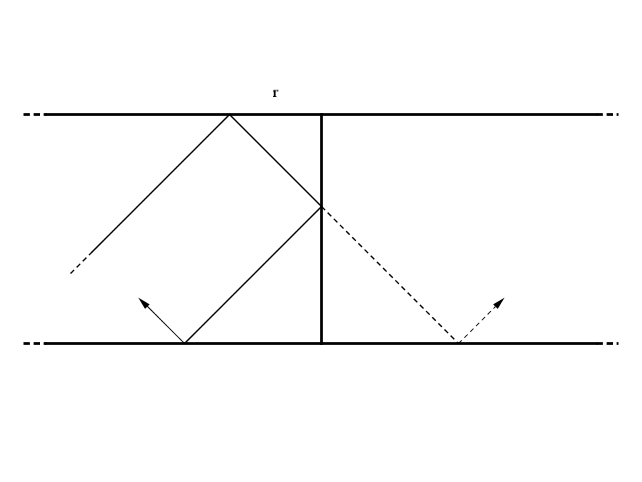
E se lo specchio fosse proprio lo Specchio di Alice, sarebbe la palla (e non la sua immagine) che continuerebbe la corsa. Ed ecco che, dopo altri $q$ rimbalzi arriverebbe alla distanza $2r$ dal lato corto successivo (precedente?)
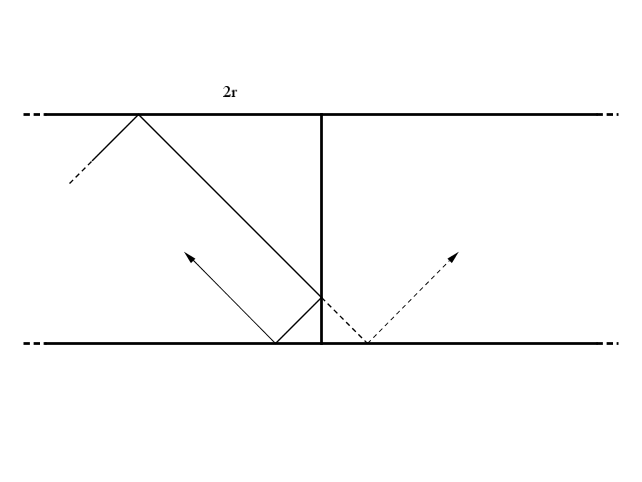
Non volendo invertire il moto della palla abbiamo sostituito anche questa sponda con uno Specchio di Alice: la palla procederà per altri $q$ rimbalzi fino ad un punto posto a $3r$ di distanza dal prossimo lato corto/Specchio di Alice.
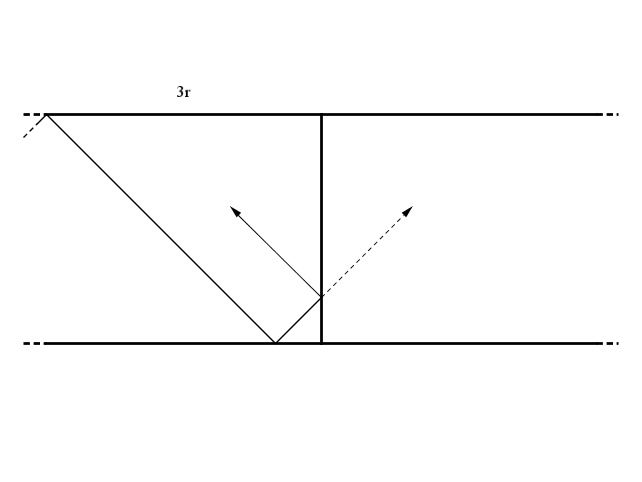
Prima del primo specchio, $r$, prima del secondo, $2r$, prima del terzo, $3r$ e così via fino a che, finalmente, prima dell'$m$-esimo specchio la distanza sarà $m \/ r$ e la palla raggiungerà l'angolo con esattamente $r$ rimbalzi.
Vediamo un esempio con $m \/ = \/ 5$ e $n \/ = \/ 7$
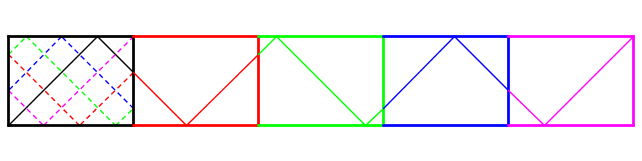
Le traiettorie sui vari tavoli riflessi e traslati (ovvero, doppiamente riflessi) sono riportate sul tavolo originale con tratteggio.
La palla subisce $m$ (contando l'ultima nell'angolo) Riflessioni di Alice e compie $m \/ \times \/ q \/ + \/ r \/ = \/ n$ rimbalzi sui lati lunghi (ho fatto un esempio con $q \/ = \/ 1$ altrimenti il disegno veniva troppo lungo e stretto)
Per capire quale sarà l'angolo colpito sovrapponiamo al piano del biliardo un reticolo unitario (unità di misura di $m$ e $n$)
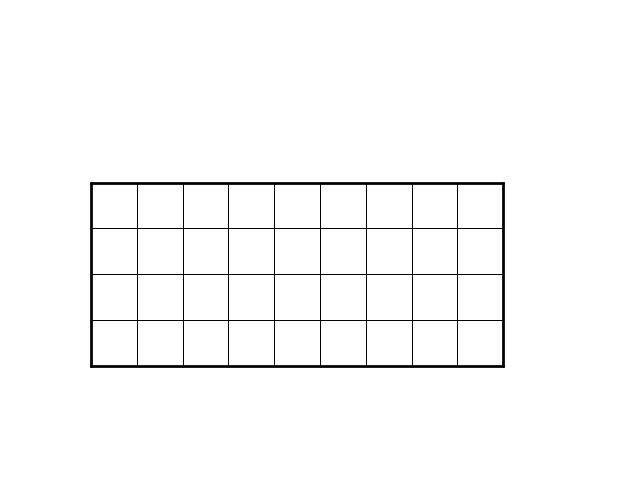
La palla, muovendosi a 45°, non può spostarsi che in punti del reticolo in cui la variazione delle due coordinate sia uguale (in modulo), cioè punti di "parità" uguale
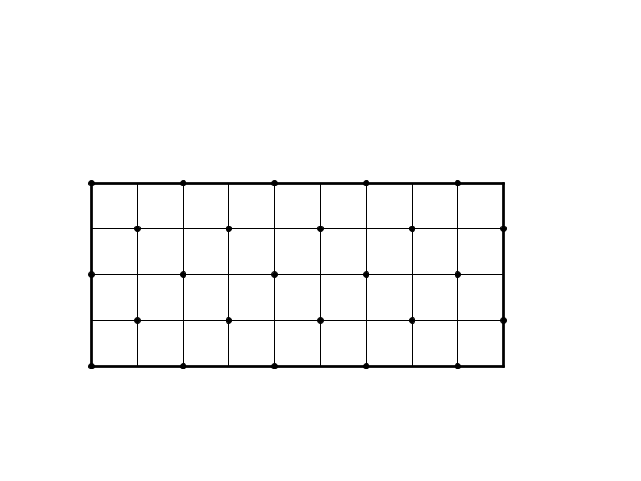
Quindi verrà raggiunto l'angolo di parità uguale: nella figura precedente il lato lungo è dispari e il lato corto è pari, nella figura successiva è vero il contrario
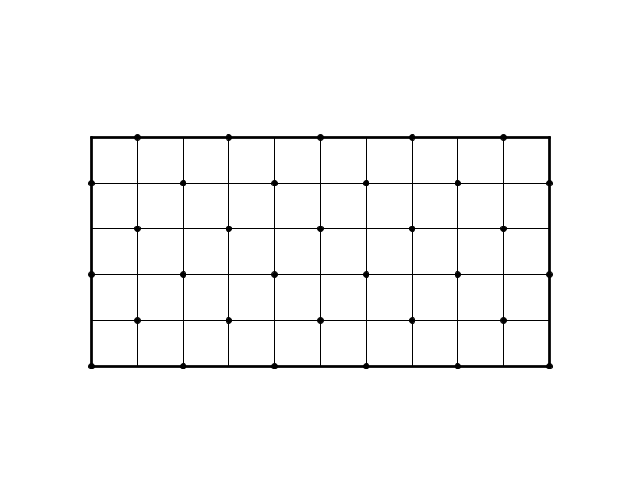
Se uno dei due lati è pari l'angolo di parità uguale è l'angolo adiacente al lato pari; se i due lati sono entrambi dispari, l'angolo di parità uguale è l'angolo opposto al centro
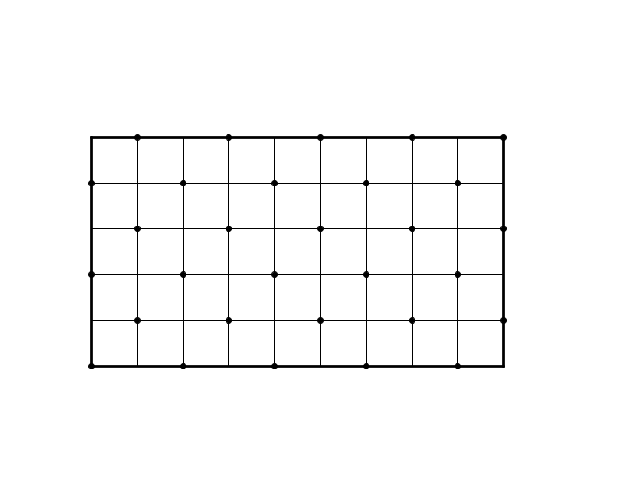
Tertium non datur: $m$ e $n$ non possono essere entrambi pari altrimenti la frazione non è ridotta ai minimi termini contro le ipotesi.
Baci
) mi c'è voluto un po' per capire: ecco, invece, il mio pacco.Consideriamo un tavolo da carambola (così evitiamo di discutere sulle dimensioni delle buche ecc.) di lati $a$ e $b$ con $a \/ < \/ b$: con questa assunzione non si ha perdita di generalità perché lo scambio di $a$ con $b$
equivale a iniziare il moto della palla dall'altro angolo adiacente al lato corto
e il piano del biliardo possiede un piano di simmetria perpendicolare passante per l'asse dei lati corti che rende equivalenti le due situazioni.
Prendiamo due numeri interi, $m$ e $n$ tali che $m/n \/ = \/ a/b$ con $m/n$ frazione ridotta i minimi termini, come misure del piano del biliardo.
Dato che il moto è a 45°, la palla percorre distanze eguali longitudinalmente e trasversalmente e al primo rimbalzo colpisce la sponda del lato lungo ad una distanza $m$ dal lato corto
Al secondo ribalzo la palla colpisce la sponda opposta ad una distanza di $2m$, al terzo, di $3m$, e così via fino a che la distanza del rimbalzo dal lato corto successivo non sarà $r \/ < \/ m$
La palla esegue, col suo moto, una divisione col resto: $n \/ = q \/ \times \/ m \/ + \/ r$.
A questo punto la palla rimbalza prima sul lato corto e poi sul lato lungo, procedendo in verso opposto.
Ma, se noi poniamo al posto della sponda uno specchio (elastico!) vedremo l'immagine riflessa della palla che prosegue la sua corsa sul biliardo speculare
E se lo specchio fosse proprio lo Specchio di Alice, sarebbe la palla (e non la sua immagine) che continuerebbe la corsa. Ed ecco che, dopo altri $q$ rimbalzi arriverebbe alla distanza $2r$ dal lato corto successivo (precedente?)
Non volendo invertire il moto della palla abbiamo sostituito anche questa sponda con uno Specchio di Alice: la palla procederà per altri $q$ rimbalzi fino ad un punto posto a $3r$ di distanza dal prossimo lato corto/Specchio di Alice.
Prima del primo specchio, $r$, prima del secondo, $2r$, prima del terzo, $3r$ e così via fino a che, finalmente, prima dell'$m$-esimo specchio la distanza sarà $m \/ r$ e la palla raggiungerà l'angolo con esattamente $r$ rimbalzi.
Vediamo un esempio con $m \/ = \/ 5$ e $n \/ = \/ 7$
Le traiettorie sui vari tavoli riflessi e traslati (ovvero, doppiamente riflessi) sono riportate sul tavolo originale con tratteggio.
La palla subisce $m$ (contando l'ultima nell'angolo) Riflessioni di Alice e compie $m \/ \times \/ q \/ + \/ r \/ = \/ n$ rimbalzi sui lati lunghi (ho fatto un esempio con $q \/ = \/ 1$ altrimenti il disegno veniva troppo lungo e stretto
)Per capire quale sarà l'angolo colpito sovrapponiamo al piano del biliardo un reticolo unitario (unità di misura di $m$ e $n$)
La palla, muovendosi a 45°, non può spostarsi che in punti del reticolo in cui la variazione delle due coordinate sia uguale (in modulo), cioè punti di "parità" uguale
Quindi verrà raggiunto l'angolo di parità uguale: nella figura precedente il lato lungo è dispari e il lato corto è pari, nella figura successiva è vero il contrario
Se uno dei due lati è pari l'angolo di parità uguale è l'angolo adiacente al lato pari; se i due lati sono entrambi dispari, l'angolo di parità uguale è l'angolo opposto al centro
Tertium non datur: $m$ e $n$ non possono essere entrambi pari altrimenti la frazione non è ridotta ai minimi termini contro le ipotesi.
Baci
il panurgo
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
Re: Scottish Book n.147
Grande Guido!
Di Franco ho già detto nell' iscritto sospetto,
ma riguardo a te... ti lascio maestro e ti ritrovo
maestro
Appena riesco vado a studiarmi la questione del
domino.
Un saluto e un abbraccio a tutti tutti!
Di Franco ho già detto nell' iscritto sospetto,
ma riguardo a te... ti lascio maestro e ti ritrovo
maestro
Appena riesco vado a studiarmi la questione del
domino.
Un saluto e un abbraccio a tutti tutti!
Bruno