Ciao boys, visto che domani primo maggio è la festa dei lavoratori, ecco un problemino facile da sbrigare in scioltezza senza sudare:

"Oggi sono da solo e ho 1 euro.Domani saremo in 9 e avremo fra tutti 17 euro.Dopodomani saremo in 36 e avremo in totale 98 euro.
Così continuando, l'ennesimo giorno saremo in $1^3+2^3+3^3+.....n^3$ (*) e avremo in totale$1^4+2^4+3^4+....n^4$ euro.
Quando arriveremo ( dividendo idealmente fra noi in parti uguali il malloppo) a superare il traguardo dei 1000 euro a testa?"

(*) avevo inizialmente scritto erroneamente 1^2+2^2... mi scuso una banale distrazione

Da "Quanti,gatti e numeri"

Buon riposo a tutti

Bye David

Beh la crescita dei soldi è una serie del tipo A = (n(n+1)(2n+1)(3n^2 +3n-1))/30 mentre quella delle persone è B = (n(n+1)/2)^2

per cui a rigor di logica credo che basti forzare il rapporto A/B > 1000 che se non ho sbagliato i conti dovrebbe essere 1250...

Giusto?

Anche io ottengo lo stesso risultato di fabtor; per la precisione mi ritrovo a dover risolvere un'equazione di terzo grado (con coefficienti spropositati, ma la calcolatrice esiste apposta per quello) per ottenere il minimo valore di n.
Il computer conferma la correttezza della soluzione, ma sono convinto che ci sia una soluzione molto più semplice e "umana", cioè che non necessita di calcolatori di sorta. Ho infatti studiato la funzione f(a, b, r) che calcola il più piccolo valore di n t.c.
$\frac{\sum_{i=1}^n i^a}{\sum_{i=1}^n i^b} \ge r$
e ho una congettura: $f(a, a-1, r)=\left\{\begin{array}{lr}2*r-1 & a=1 \\ \left[r+\frac{r}{a}\right] & altrimenti\\ \end{array}\right.$

Sì, anch'io inizialmente avevo ottenuto l'equazione di cui parli, per questo ho poi deciso di risolverla per via grafica sfruttando i risultati del rapporto di serie.

Inoltre anche secondo me ci deve essere una soluzione meno "laborioriosa" dal punro di ista del calcolo, tuttavia al momento non ho avuto il tempo di ragionarci troppo su (era domenica quando mi ci sono messo ed ero pure incastrato tra due feste della mamma ). Appena ho un po' più di tempo mi ci scervellerò un po' su...

Ciao.

Sono arrivato allo stesso risultato, ma con un ragionamento diverso.

David ha scritto:...saremo in $1^3+2^3+3^3+.....n^3$ (*) e avremo in totale$1^4+2^4+3^4+....n^4$ euro.

Entrambe queste serie hanno un andamento crescente ordinato assimilabili all'integrale di due funzioni, rispettivamente l'integrale di $X^3$ per quanto riguarda le persone e di $X^4$ per quanto riguarda gli euro.
Dobbiamo quindi trovare quando (ovvero in che dominio) l'integrale di $X^4$ è uguale a 1000 * l'integrale di $X^3$
L'integrale di $X^4$ è $(X^5)/5$, e l'integrale di $X^3$ è $(X^4)/4$
Quindi basta risolvere l'equazione:
$X^5/5=1000 x^4/4$
Semplificando le due $X^4$ si ha X (ovvero il dominio) = 5 * 1000 / 4 = 1250

Spero che la spiegazione sia chiara, il tex poi non lo ricordo bene...

Purtroppo sono di corsa. Ho visto il problema di
David stamattina e lo risolverei così, solo con
carta e penna, con mezzi elementari e direi anche
in maniera abbastanza "svelta" (nel senso che
con un po' di spirito di osservazione non c'è
affatto bisogno di perdersi in calcoli o passaggi
laboriosi, richiamandomi alle considerzioni espresse
qui sopra da Fabtor).

Allora, scrivo esplicitamente il rapporto indicato
dal nostro Fabtor:

${\small 2\,(2n+1)}\,\(\frac 1 5-\frac {1}{15n(n+1)}\)$

e poi osservo che:

${\small (2\cdot 1250+1)}\,\(\frac 1 5-\frac {1}{15\cdot 1250\cdot 1251}\) \,>\,{\small (2\cdot 1250+1)}\,\[\frac 1 5-\frac {1}{10^5 {\tiny (=80\cdot 1250)}}\]\,>\, 500 \,>\, {\small (2\cdot 1249+1)}\,\frac 1 5 \;.$

Le ultime due disuguaglianze sono senz'altro
soddisfatte. Da esse infatti, nell'ordine, si
deducono agilmente le seguenti:

$\quad\Rightarrow\quad\; (500\cdot 5 +1)(500\cdot 40-1) \,>\, 500\cdot 10^5\,=\, 500\cdot 500\cdot 5\cdot 40 \\\,\\ \quad\Rightarrow\quad \; 2\cdot 1250 \,>\, 2\cdot 1249+1$

(Salvo sviste.)

X Bautz:
Ottimo direi!!! Mi hai battuto sul tempo!!!

Direi che questa oltre ad essere la soluzione meno laboriosa è anche la più elegante possibile.

L'unica considerazione che mi lascia vagamente perplesso e che stavo appunto vagliando è la seguente:

Col passaggio dalle serie agli integrali si ottiene che per 1250 persone si hanno precisamente 1000 euro a testa mentre rimanendo alle serie la quantità reale di soldi risulta essere leggermente maggiore (40 centesimi in più), quindi stando al testo del problema che chiedeva con quante persone si superavano i 1000 euro a testa mi verrebbe da dire che mentre con la "soluzione seriale" tale numero è proprio 1250 con la "soluzione integrale" si dovrebbe conludere che tale numero dovrebbe a rigor di logica essere portato a 1251 (anche se in fin dei conti con la soluzione integrale su 1250 persone si "perdono" solo 5 euro cioè solo il $4X10^{-4}%$).

X Tutti:

Quindi non posso non chiedermi quanto: in generale, quando si usa il passaggio dalle serie agli integrali, seppur lecitamente come in questo caso, come discutere i risultati che si ottengono senza verificarli proprio per mezzo del calcolo seriale?
O meglio c'è qualcosa che ci possa permettere di dire al "risultato integrale" decurta (o magari aggiungi) un'unità (o un k opportunamente piccolo riferito all'unità di misura della grandezza che si sta valutando) per ottenere il risultato reale?

fabtor ha scritto:...mi verrebbe da dire che mentre con la "soluzione seriale" tale numero è proprio 1250 con la "soluzione integrale" si dovrebbe conludere che tale numero dovrebbe a rigor di logica essere portato a 1251...

Nella mia soluzione c'è un errore... risolverlo forse serve a sciogliere il problema che hai posto.
L'integrale che ho utilizzato per approssimare entrambe le serie è infatti sbagliato!
Prendiamo una serie $1^n+2^n+3^n+...$ tipo

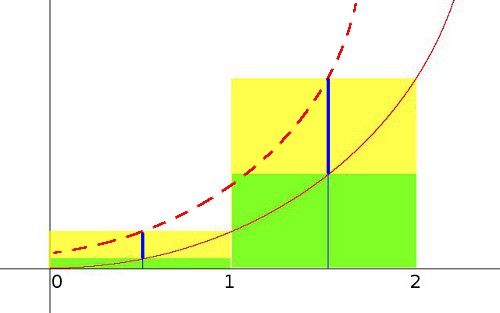
In giallo (o meglio, giallo + verde) ho indicato la superficie della serie tipo $1^n+2^n+3^n+...$.
In rosso sottile continuo ho indicato la curva che nella soluzione precedente ho dato come approssimazione per l'integrale.
Ma in realtà quella curva, cioè $x^n$, approssima l'integrale della serie rappresentata dai rettangoli verdi!
Per ottenere la curva che approssima la vera serie (cioè verde + giallo) bisogna spostare la curva di mezza unità verso sinistra (edit: avevo erroneamente scritto destra) sul grafico, cioè la curva rossa tratteggiata, quindi invece di integrare $x^n$ bisogna integrare $(x+1/2)^n$.
Perciò tornando all'esempio richiesto, la prima serie è assimilabile all'integrale di $(x+1/2)^4$ e la seconda serie all'integrale di $(x+1/2)^3$.
quindi si ha che:
$[(x+1/2)^5]/5=[(x+1/2)^4]/4$
e quindi
$x+1/2=1250$
cioè
$x=1249,5$

Quindi si raggiungono i 1000 euro a testa con 1249 persone, ovvero si superano con 1250

Si, con la correzione che hai inserito i conti ora tornano tuttavia rimane un problema (secondo me):

Come giustificare, senza passare per via grafica, che $\sum_{k=0}^{n}$$x^{k}$ è assimilabile a $\int_{0}^{n}$$(x + \frac{1}{2})^{k}$ e non a $\int_{0}^{n}$$x^{k}$ ?

O generalizzando, come trovare il valore h$\in$ R tale che:

essendo$\sum_{k=0}^{n}$$x^{k}$ non assimilabile a$\int_{0}^{n}$$x^{k}$

sia $x^{k}$ $\sum_{k=0}^{n}$$x^{k}$ sia assimilabile a $\int_{0}^{n}$$(x + h)^{k}$ ?

O meglio ancora come trovare il valore di h $\in$ R affinchè:

$x^{k}$ $\sum_{k=0}^{n}$$x^{k}$ sia assimilabile a $\int_{0}^{n}$$(x + h)^{k}$ ?

fabtor ha scritto:Come giustificare, senza passare per via grafica, che $\sum_{k=0}^{n}$$x^{k}$ è assimilabile a $\int_{0}^{n}$$(x + \frac{1}{2})^{k}$ e non a $\int_{0}^{n}$$x^{k}$ ?
...
O meglio ancora come trovare il valore di h $\in$ R

Quel valore $h$, nell'approssimare $\sum_{k=0}^{n}x^{k}$ a $\int_{0}^{n}$$(x + h)^{k}$, sarà sempre $1/2$ per qualsiasi $k$ si prenda.
Provo a spiegarmi.
La definizione di integrale (di Riemann) parte dall'ipotesi di suddividere l'area sottesa alla curva in $n$ rettangoli con la stessa base, e con altezza corrispondente al valore che la funzione assume nell'ordinata corrispondente alla mezzaria della base del rettangolo.
Nel nostro caso, avendo diviso in rettangoli di base 1, la mezzaria è sempre la mezza unità.
Quindi il primo rettangolo, da 0 a 1, avrà l'altezza data dalla funzione in 0,5.
Il secondo rettangolo, da 1 a 2, avrà l'altezza data dalla funzione in 1,5, e così via.
Precedentemente, sbagliando, avevo considerato l'altezza dei rettangoli nel punto a destra.
Quindi per il primo rettangolo, da 0 a 1, avevo considerato l'altezza data dalla funzione in 1. Ma appunto l'integrale non si calcola nel punto di destra del rettangolo ma al centro. Indifferentemente dalla funzione utilizzata. Non so se riesco a spiegarmi.
Nel grafico precedente ho indicato la mezzaria dei rettangoli cercati in blu.
Nella formula sbagliata ho integrato la curva che passa per i punti di destra nel rettangolo. Nella funzione giusta invece ho preso in considerazione la funzione passante per la mezzaria dei rettangoli, quindi spostando la funziona a sinistra per un valore pari alla metà della base del rettangolo.
E visto che la serie è suddivisa in intervalli di una unità, la metà sarà la mezza unità.
Quindi nell'approssimare $\sum_{k=0}^{n}x^{k}$
a $\int_{0}^{n}$$(x + h)^{k}$
$h$ è sempre $1/2$
per qualsiasi $k$

anzi, si può generalizzare e dire si può approssimare qualsiasi serie $\sum_{k=0}^{n}f(x,k)$
all'integrale $\int_{0}^{n}$$f((x+1/2),k)$

Si sei stato chiarissimo, anche se onestamente faccio cmq fatica a digerire quell'1/2 passando dalle serie agli integrali... me ne
farò una ragione!