Dopo la somma di coseni posto una sommatoria...mista.Dimostrare che :
$\large \sum_{k=0^o}^{k=88^o}\frac{1}{\cos{k}\cos{(k+1^o})}=\frac{\cos(1^o)}{\sin^2(1^o)}$
N.B. Gli angoli sono espressi in gradi sessagesimali e non in radianti.
La ricerca ha trovato 100 risultati
- sab nov 12, 2011 6:27 pm
- Forum: Il Forum
- Argomento: Nuova sommatoria
- Risposte: 2
- Visite : 3067
- sab nov 12, 2011 6:09 pm
- Forum: Il Forum
- Argomento: Somma algebrica di coseni
- Risposte: 6
- Visite : 5160
Re: Somma algebrica di coseni
Bene Vittorio .Notevole quella formula...
- ven nov 04, 2011 4:06 pm
- Forum: Il Forum
- Argomento: Divisione di polinomi
- Risposte: 7
- Visite : 6299
Re: Divisione di polinomi
Credo che nei commenti di polarprof ci sia qualche refuso.Va bene come abbiamo fatto noi...
Complimenti per il disegno !
Complimenti per il disegno !
- gio nov 03, 2011 9:20 pm
- Forum: Il Forum
- Argomento: Divisione di polinomi
- Risposte: 7
- Visite : 6299
Re: Divisione di polinomi
Lo schema è del prof.Giovanni Artico ( che scherzosamente ama farsi chiamare "polarprof" !)
Lo puoi trovare sul sito CENTRO RICERCHE DIDATTICHE U.MORIN
Ti passo il link corrispondente ( sperando che funzioni...).Saluti
$[tex]$http://www.centromorin.it/aspnuke207/ar ... d=5&page=2[/tex]
Lo puoi trovare sul sito CENTRO RICERCHE DIDATTICHE U.MORIN
Ti passo il link corrispondente ( sperando che funzioni...).Saluti
$[tex]$http://www.centromorin.it/aspnuke207/ar ... d=5&page=2[/tex]
Re: Equazione
Ottima soluzione .Io mi ero affidato alla formula del radicale quadratico doppio,ma così è più veloce.Quanto alla verifica diretta ,credo che ci si possa limitare alle prime due radici dato che la terza è negativa e non soddisfa la condizione x>=1
Ciao
Ciao
- gio nov 03, 2011 12:06 am
- Forum: Il Forum
- Argomento: Divisione di polinomi
- Risposte: 7
- Visite : 6299
Re: Divisione di polinomi
Il metodo esposto da Pasquale è quello correntemente adoperato in algebra elementare.Io ho solo voluto
indicare una... simpatica estensione della familiare regola di Ruffini che non vuole assolutamente sostituire
quella usata da sempre... Insomma prendete la cosa come un divertente diversivo
indicare una... simpatica estensione della familiare regola di Ruffini che non vuole assolutamente sostituire
quella usata da sempre... Insomma prendete la cosa come un divertente diversivo
- mer nov 02, 2011 6:44 pm
- Forum: Il Forum
- Argomento: Divisione di polinomi
- Risposte: 7
- Visite : 6299
Divisione di polinomi
http://imageshack.us/photo/my-images/233/figxx.png/ Una curiosa generalizzazione della nota regola di Ruffini.Presumo sia già nota.Sia come sia,eccola. Si voglia eseguire la divisione: \large (x^4+5x^3+2x^2-15):(x^2-2x+3) A) I due polinomi devono essere ordinati secondo le potenze decrescenti della...
Equazione
Risolvere in R l'equazione seguente :
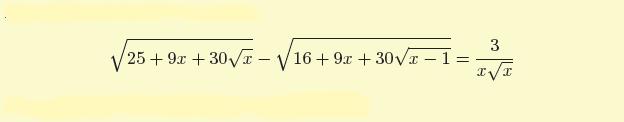
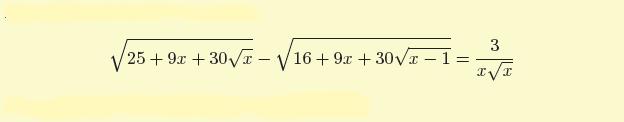
- sab ott 29, 2011 6:06 pm
- Forum: Il Forum
- Argomento: Somma algebrica di coseni
- Risposte: 6
- Visite : 5160
Re: Somma algebrica di coseni
Confesso che i calcoli approssimati mi trasmettono sempre una vaga sensazione di incertezza ! Volendo una soluzione esatta si può far ricorso,come forse traspare anche dalla forma del quesito,alle radici settime di 1 e al fatto che ,a parte l'unica radice reale che è appunto 1,le altre 6 si dividono...
- sab ott 29, 2011 5:52 pm
- Forum: Il Forum
- Argomento: Un problema di minimo
- Risposte: 22
- Visite : 16373
Re: Un problema di minimo
Non vedo perché si dovrebbe eliminare il file ( a meno che non ci sia un motivo legato al funzionamento del Forum...) .Personalmente resto affascinato da questi punti che si possono spostare ! Se a qualcuno interessa , mostro anche una soluzione elementare . Premessa. Siano p e q due reali positivi ...
- gio ott 27, 2011 8:25 pm
- Forum: Il Forum
- Argomento: Somma algebrica di coseni
- Risposte: 6
- Visite : 5160
Somma algebrica di coseni
Dimostrare che risulta :
$\fbox{\large \cos(\frac{\pi}{7})-\cos(\frac{2\pi}{7})+\cos(\frac{3\pi}{7})=\frac{1}{2}}$
In questo caso "dimostrare" significa che non ci si deve limitare ad una semplice verifica con la calcolatrice !
$\fbox{\large \cos(\frac{\pi}{7})-\cos(\frac{2\pi}{7})+\cos(\frac{3\pi}{7})=\frac{1}{2}}$
In questo caso "dimostrare" significa che non ci si deve limitare ad una semplice verifica con la calcolatrice !
- mar ott 25, 2011 5:14 pm
- Forum: Il Forum
- Argomento: Un problema di minimo
- Risposte: 22
- Visite : 16373
Re: Un problema di minimo
Secondo me l'uso delle derivate richiede che si tenga conto della condizione: \large ap+bq+cr =2S avendo indicato con S l'area del triangolo ,con a,b,c le misure dei lati e con p,q,r le misure delle rispettive distanze di P da essi. In tal modo,usando il metodo di Lagrange,la funzione da "estremizza...
- lun ott 24, 2011 7:20 pm
- Forum: Il Forum
- Argomento: Un problema di minimo
- Risposte: 22
- Visite : 16373
Re: Un problema di minimo
E' così:l'incentro risolve il problema.Resta da dimostrarlo.Con riga e compasso non saprei.
Volendo si può dimostrare con l'Analisi ( minimo condizionato) ma si risolve anche elementarmente...
Volendo si può dimostrare con l'Analisi ( minimo condizionato) ma si risolve anche elementarmente...
- ven ott 21, 2011 6:34 pm
- Forum: Il Forum
- Argomento: Un problema di minimo
- Risposte: 22
- Visite : 16373
Un problema di minimo
Sia ABC un triangolo e P un punto ad esso interno.Dette D,E,F le proiezioni di P su i lati
BC,CA,AB rispettivamente ,si determini la posizione di P per la quale è minima la somma:
$\large \frac{AB}{PF} +\frac{BC}{PD} +\frac{CA}{PE}$
BC,CA,AB rispettivamente ,si determini la posizione di P per la quale è minima la somma:
$\large \frac{AB}{PF} +\frac{BC}{PD} +\frac{CA}{PE}$
- sab ott 15, 2011 5:55 pm
- Forum: Il Forum
- Argomento: Quadrilatero ed angoli
- Risposte: 9
- Visite : 7321
Quadrilatero ed angoli
Sia ABCD un quadrilatero con l'angolo CBD doppio dell'angolo ADB e l'angolo ABD doppio dell'angolo CDB.Sapendo che AB=CB dimostrare che è pure AD=CD .
