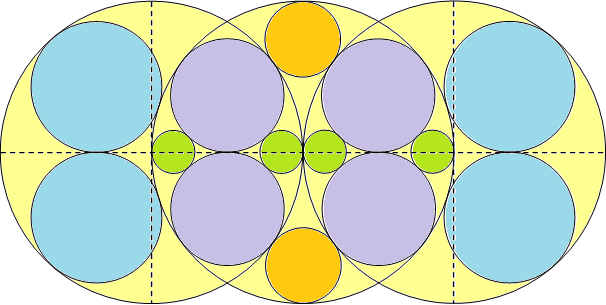
Secondo step: Modificando leggermente la disposizione precedente si riesce a ridurre a 11 il numero di fori necessari per impedire di ricavare l'etichetta. . https://i.postimg.cc/q7jtkFFQ/Due-cerchi-2.png Deve perciò essere n < 11. Il terzo step è il più complicato. Bisogna trovare una disposizione ...

Bel lavoro, Franco. ... disegnando archi di circonferenza anzichè poligoni ... E' interessante notare che, in questo caso, l'area massima si ha quando la distanza tra i centri dei due cerchi è uguale al raggio dei cerchi come in figura. . https://i.postimg.cc/bJ86sR52/Due-cerchi.png L'area massima d...

... Non mi torna ... se non ho sbagliato i conti, la tua formula equivale a circa $31,6 m^2$. Facendo due semplici recinti poligonali regolari a 20 lati, la superficie totale è di oltre $252 m^2$ Franco, hai ragione. Panurgo ha considerato l'area di un solo recinto a forma di poligono regolare di 2...

Problema interessante e abbastanza impegnativo [****]. Considerazioni preliminari: Cominciamo col porre un limite superiore ad n. E' evidente che per n = 12 o superiore non posso essere sicuro che sia rimasto uno spazio per la mia etichetta. Infatti se i 12 fori sono disposti su una griglia rettango...

Vista l'affinità posto qui un semplice problema tipo "Sangaku".
Trovare i raggi dei cerchi colorati sapendo che il raggio dei tre cerchi esterni è 1.
. .

... La classifica è, le prime 2 righe ammettono permutazioni,: $ \displaystyle \begin{array}{|c|c|c|c|c|c|} \hline & Alberto & Bruno & Carlo & Dario \\ \hline Prova_1 & 7 & 3 & 2 & 1 \\ \hline Prova_2 & 8 & 10 &4 & 4 \\ \hline Prova_3 & 11 & 11 & 6 & 11 \\ \hline Prova_4 & 14 & 13 & 13 & 12 \\ \hli...

Riprendo questo vecchio problema per proporre una nuova variante. All'interno di un triangolo rettangolo vi è un punto P le cui distanze dai tre vertici del triangolo sono 5, 7, 8. - Trovare l'area del triangolo se esso è anche isoscele. - Trovare l'area massima del triangolo. - Generalizzare nel ca...

Quelo ha scritto: ↑

dom mar 16, 2025 11:49 am

Correggi l'errore

23 − 3 × 6 = 5!

(23 - 3) x 6 = 5! = 120

Questi facili quesiti sono presi dalla homepage di base 5 [A25-20]. L'unico simbolo non utilizzabile è $\neq$ (cioè barrare il simbolo =). . https://i.postimg.cc/vHyh5QnH/trattino.png . Il primo, molto facile, l'ho risolto io (trattino rosso) ma non escludo che ci siano altre soluzioni più originali.

... Deterimnare: - il numero n delle prove ... Alla fine del concorso sono stati assegnati 20 + 17 + 15 + 13 = 65 punti. Il punteggio totale può essere scomposto in 13 x 5 per cui o le prove sono state 5 e in ognuna sono stati assegnati 13 punti totali oppure le prove sono 13 e in ognuna sono stati...

Quelo ha scritto: ↑

dom feb 16, 2025 11:27 pm

... Il massimo di quadrati che si può ottenere è 6 su 10

Io ho trovato due soluzioni. La prima è: La seconda è (2,15,34,47,66).
Nella prima i quadrati sono tutti diversi mentre nella seconda ci sono due 49 e due 81.

Può essere di aiuto questa bella dissezione.

Quelo ha scritto: ↑

gio feb 13, 2025 9:44 pm

...
I tuoi risultati mi hanno indotto a ripensare l'algoritmo di ricerca e sono emersi diversi quadrati, questo è quello minimo
...

Python colpisce ancora!

Ed eccone un altro.

Quelo ha scritto: ↑

lun feb 10, 2025 9:17 pm

...
Esiste un "quadrato magico al quadrato" 2x2 (in cui le somme di righe, colonne e diagonali sono quadrati perfetti)?

Certo che esiste!