Good! Grazie a Karl e Base5.

Chapeau, karl!

Per noi poveri analitici (al liceo ho "studiato" solo geometria analitica) l'efficacia di questa dimostrazione è stupefacente. Mi permetto di aggiungere qualcosa del mio: generalizziamo il problema togliendo il vincolo che l'angolo in ${\text D}$ sia retto.

E’ intuitivamente ovvio che un triangolo sia determinato se conosciamo due angoli e il lato tra loro compreso; per ottenerlo è sufficiente tracciare il lato e due semirette opportunamente angolate che si incontreranno nel terzo vertice.
Dal punto di vista del calcolo si distinguono tre casi: a) entrambi gli angoli sono acuti, b) uno dei due angoli è retto e c) uno dei due angoli è ottuso



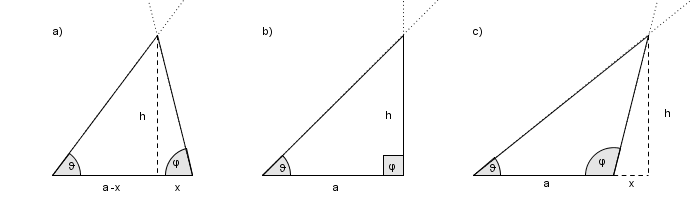
Nel primo caso abbiamo

$h\/=\/\left(a\/-\/x\right)\/\tan\vartheta\/=\/x\/tan\varphi$

da cui segue

$x\/=\/a\frac{\tan\vartheta}{\tan\varphi+\tan\vartheta}$

e

$A\/=\/\frac{ah}2\/=\/\frac{a^{\script 2}}2\frac{\tan\varphi\tan\vartheta}{\tan\varphi+\tan\vartheta}$

Nel secondo caso abbiamo

$h\/=\/a\/\tan\vartheta$

e

$A\/=\/\frac{a^{\script 2}}2\tan\vartheta$

Infine, nel terzo caso, abbiamo (si veda qui per l’uso di $\tau$ al posto di $\pi$)

$h\/=\/\left(a\/+\/x\right)\/\tan\vartheta\/=\/x\/\tan\left(\frac\tau2\/-\/\varphi\right)\/=\/-\/x\/\tan\varphi$

da cui seguono

$x\/=\/-\/a\frac{\tan\vartheta}{\tan\varphi+\tan\vartheta} \\ A\/=\/\frac{a^{\script 2}}2\frac{\tan\varphi\tan\vartheta}{\tan\varphi+\tan\vartheta}$

la stessa espressione del primo caso.
Concludiamo che, dati due angoli e il lato compreso, l’area del triangolo vale

$A\left(a,\vartheta,\varphi\right)\/=\/\left\{\begin{array}{l100lC40+}\frac{a^{\script 2}}2\tan\vartheta & \varphi\/=\/\frac\tau4 \\ \frac{a^{\script 2}}2\frac{\tan\varphi\tan\vartheta}{\tan\varphi+\tan\vartheta} & \varphi\/\neq\/\frac\tau4 \end{arra}\right.$

Veniamo ora al nostro triangolo.
Poniamo $\angle{\text CBA}\/=\/\beta$ e $\angle{\text EDA}\/=\/\delta$ con $\overline{\text AD}\/=\overline{\text CE}\/=\/d$



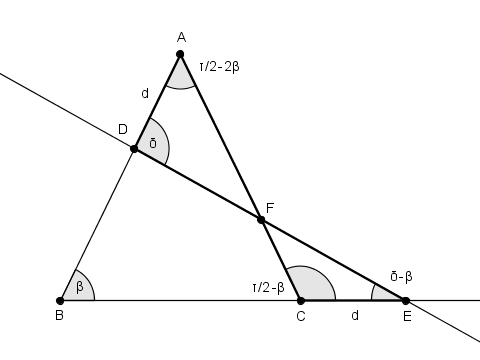
e troviamo che $\angle{\text BAC}\/=\/\tau/2\/-\/2\beta$, $\angle{\text ECA}\/=\/\tau/2\/-\/\beta$ e $\angle{\text DEB}\/=\/\delta\/-\/\beta$.
Dei triangoli ${\text ADF}$ e ${\text CEF}$ conosciamo dunque due angoli e il lato compreso e possiamo quindi utilizzare le formule trovate prima.
Il triangolo ${\text CEF}$ è sempre ottusangolo ma il triangolo ${\text ADF}$ può anche essere rettangolo quindi dobbiamo distinguere due casi: per $\delta\/\neq\/\tau/4$ abbiamo

$\begin{array}{lC60+} {\text ADF}\/=\/\frac{d^{\script 2}}2\/\frac{\tan\left(\tau/2-2\beta\right)\tan\delta}{\tan\left(\tau/2-2\beta\right)+\tan\delta}\/=\/\frac{d^{\script 2}}2\/\frac{-\tan2\beta\tan\delta}{-\tan2\beta+\tan\delta} \\ {\text CEF}\/=\/\frac{d^{\script 2}}2\/\frac{\tan\left(\tau/2-\beta\right)\tan\left(\delta-\beta\right)}{\tan\left(\tau/2-\beta\right)+\tan\left(\delta-\beta\right)}\/=\/\frac{d^{\script 2}}2\/\frac{-\tan\beta\tan\left(\delta-\beta\right)}{-\tan\beta+\tan\left(\delta-\beta\right)} \end{array}$

Considerando che

$\begin{array}{lC40+} \tan2\beta\/=\/\frac{2\tan\beta}{1-\tan^{\script 2}\beta} \\ \tan\left(\delta\/-\/\beta\right)\/=\/\frac{\tan\delta-\tan\beta}{1+\tan\delta\tan\beta} \end{array}$

e ponendo $t\/=\/\tan\beta$ e $u\/=\/\tan\delta$ otteniamo

$\begin{array}{lC80+} {\text ADF}\/=\/\frac{d^{\script 2}}2\/\frac{-\frac{2\tan\beta}{1-\tan^{\script 2}\beta} \tan\delta}{-\frac{2\tan\beta}{1-\tan^{\script 2}\beta} +\tan\delta}\/=\/ d^{\script 2}\/\frac{ut}{2t-u+ut^{\script 2}} \\ {\text CEF}\/=\/\frac {d^{\script 2}} 2\/\frac {-\tan\beta\frac{\tan\delta-\tan\beta}{1+\tan\delta\tan\beta}} {-\tan\beta+\frac{\tan\delta-\tan\beta}{1+\tan\delta\tan\beta}}\/=\/ \frac {d^{\script 2}}2\/\frac{t\left(u-t\right)}{2t-u+ut^{\script 2}} \end{array}$

Poniamo ora ${\text ADF}\/=\/2{\text CEF}$ e otteniamo $ut\/=\/t\left(u\/-\/t\right)$ da cui segue $t\/=\/\tan\beta\/=\/0$ e quindi $\beta\/=\/0$.
Non ci resta che sperare in $\delta\/=\/\tau/4$. In questo caso abbiamo $\angle{\text DEB}\/=\/\tau/4\/-\/\beta$.



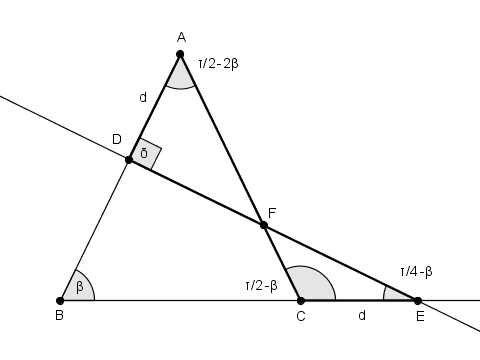
e

$\begin{array}{lC40+} {\text ADF}\/=\/ \frac {d^{\script 2}} 2 \/ \tan \left(\tau/2\/-\/2\beta\right)\/=\/ -\/\frac {d^{\script 2}} 2 \/ \tan \left(2\beta\right)\/=\/ d^{\script 2}\/\frac t{t^{\script 2}-1} \\ {\text CEF}\/=\/ \frac {d^{\script 2}}2\/\frac{\tan\left(\tau/2-\beta\right)\tan\left(\tau/4-\beta\right)} {\tan\left(\tau/2-\beta\right) +\tan\left(\tau/4-\beta\right)}\/=\/ \frac{d^{\script 2}}2\/\frac{-\tan\beta\cot\beta}{-\tan\beta+\cot\beta}\/=\/ \frac {d^{\script 2}}2\/\frac1{t-1/t}\/=\/ \frac{d^{\script 2}}2\/\frac t{t^{\script 2}-1}\/=\/ \frac{\text ADF}2 \end{array}$

QED

panurgo ha scritto:Chapeau, karl!

Per noi poveri analitici (al liceo ho "studiato" solo geometria analitica) l'efficacia di questa dimostrazione è stupefacente. [...]

Condivido l'entusiasmo per la dimostrazione di Karl...
Che cosa intendi esattamente con le parole al liceo ho "studiato" solo geometria analitica? Quale liceo hai frequentato?
Intendi dire semplicemente che non eri interessato alla risoluzione degli esercizi di geometria sintetica?
Di certo so che (almeno fino a 25 anni fa!) nei primi due anni del liceo scientifico i manuali di geometria riportavano una consistente raccolta di esercizi consistenti in teoremi da dimostrare e da risolvere graficamente senza che fossero richieste, per la risoluzione, conoscenze di carattere algebrico...

Ivana ha scritto:Che cosa intendi esattamente con le parole al liceo ho "studiato" solo geometria analitica? Quale liceo hai frequentato?

Un liceo sperimentale in cui il latino era opzionale e poteva essere sostituito con la seconda lingua straniera (Я гаварю па русский )...

Un lavoraccio enorme, ma pulito, la dimostrazione di Pan: quello che avevo cercato di fare per altre vie, senza successo.

L'accenno alla geometria analitica mi fa pensare che debba essercene bisogno per la risoluzione del primo problema, che non ancora riesco ad inquadrare: finora ho visto che, dando dei valori ad a,b,c,d,e,f, si trovano tre parabole tali che i loro rami, intersecandosi, racchiudono una porzione del piano di una certa forma e dimensione.
Non so se è questo che intende il testo, ma se lo è, non mi pare facile dimostrare quello che viene richiesto.
Mi pare che questi quesiti siano abbastanza tostarelli.

[img]http://imageshack.us/photo/my-images/842/pasqualel.jpg/[/img]

Le tre parabole (vedere figura allegata) s'incontrano a due a due in un unico punto
(proprio).Le ascisse di questi tre punti sono date dalle formule:

$\displaystyle x_A=\frac{d-b}{a-c}$

$\displaystyle x_B=\frac{f-d}{c-e}$

$\displaystyle x_C=\frac{b-f}{e-a}$

Per avere l'area S racchiusa dalle 3 parabole ( quella in rosso nella fig.) occorre
integrare in senso antiorario lungo il contorno di essa a partire da un vertice qualunque ( ad es. A)
Pertanto:


$\displaystyle S=|\frac{1}{3}x^3+\frac{1}{2}cx^2+dx|_{x_A}^{x_B}+$$\displaystyle |\frac{1}{3}x^3+\frac{1}{2}ex^2+fx|_{x_B}^{x_C}+$$|\frac{1}{3}x^3+\frac{1}{2}ax^2+bx|_{x_C}^{x_A}$

Per facilitare gli sviluppi successivi conviene dividere il calcolo in 3 parti ,una per ogni potenza della x:


$\displaystyle S_3=\frac{1}{3}[(x_B^3-x_A^3)+(x_C^3-x_B^3)+(x_A^3-x_C^3)]$ =0


$\displaystyle S_2=\frac{1}{2}[c(x_B^2-x_A^2)+e(x_C^2-x_B^2)+a(x_A^2-x_C^2)]$=

=$\frac{1}{2}[(a-c)x_A^2+(c-e)x_B^2+(e-a)x_C^2]=$$\displaystyle \frac{1}{2}[\frac{(d-b)^2}{a-c}+\frac{(f-d)^2}{c-e}+\frac{(b-f)^2}{e-a}]$

$\displaystyle S_1=d(x_B-x_A)+f(x_C-x_B)+b(x_A-x_C)=x_A(b-d)+x_B(d-f)+x_C(f-b)=-\frac{(d-b)^2}{a-c}-\frac{(f-d)^2}{c-e}-\frac{(b-f)^2}{e-a}$

Sommando :

$\displaystyle S=\frac{1}{2}[-\c \frac{(d-b)^2}{a-c}-\frac{(f-d)^2}{c-e}-\frac{(b-f)^2}{e-a}]=\frac{1}{2}[- \frac{(d-b)^2}{a-c}-\frac{(f-d)^2}{c-e}+\frac{(b-f)^2}{a-e}]$

Come si vede S è razionale.Quanto alla seconda questione ,possiamo supporre a>c>e ( a questo ci si può sempre
ricondurre con un opportuno riordinamento delle equazioni delle 3 parabole ).Allora si vede che,riducendo S
ad un'unica frazione ,il denominatore D è del tipo :

$\displaystyle D= 2(a-c)(c-e)(a-e)$

Per AM-GM risulta :

$\displaystyle D \le 2\cdot \frac{(a-c+c-e+a-e)^3}{3^3}=16\cdot (\frac{a-e}{3})^3$

Ma max(a-e)=14 e quindi:

$\displaystyle D\le 16\cdot (\frac{14}{3})^3<16\cdot (\frac{15}{3})^3=2000$