Le noccioline
Moderatori: Gianfranco, Bruno
Questo forum è una sezione del PORTALE DI BASE CINQUE
Ripropongo nuovamente questo vecchio topic di microproblemi per non aprire un nuovo topic solo per questo quesito veloce e simpatico.
Brevemente: un manipolo di legionari scende nel campo di battaglia, coi soldati disposti nella classica formazione a quadrato. Dopo un assalto delle truppe avversarie cade l'intera prima fila di uomini e dopo un secondo attacco ne cadono altri otto. I restanti legionari si ridispongono a formare un quadrato. Quanti erano i legionari all'inizio della battaglia?
Forse esiste una soluzione immediata e ovvia ma io ne ho trovata solo una lunga e calcolosa... chi sa aiutarmi?
Buonanotte a tutti
Zerinf
Brevemente: un manipolo di legionari scende nel campo di battaglia, coi soldati disposti nella classica formazione a quadrato. Dopo un assalto delle truppe avversarie cade l'intera prima fila di uomini e dopo un secondo attacco ne cadono altri otto. I restanti legionari si ridispongono a formare un quadrato. Quanti erano i legionari all'inizio della battaglia?
Forse esiste una soluzione immediata e ovvia ma io ne ho trovata solo una lunga e calcolosa... chi sa aiutarmi?
Buonanotte a tutti
Zerinf
Lo scopo principale di una dichiarazione DATA è quello di dare dei nomi alle costanti; anziché inserire ogni volta 3.141592653589793 come valore di $\pi$, con una dichiarazione DATA si può assegnare tale valore alla variabile PI che può essere poi usata per indicare la costante. Ciò rende anche più semplice modificare il programma, qualora il valore di $\pi$ dovesse cambiare.
-Da un vecchio manuale FORTRAN della Xerox
-Da un vecchio manuale FORTRAN della Xerox
Visto che 16 mi sembra un numero piuttosto esiguo (anche se trattasi di manipolo) direi che erano 81 disposti 9x9, dopo il primo assalto cadono i 9 della prima fila e ne rimangono 72, dopo il secondo assalto ne rimangono 64 che si ridristribuiscono 8x8.
In alternativa erano più di 1.000.000 che è fin dove ho controllato.
In alternativa erano più di 1.000.000 che è fin dove ho controllato.
[Sergio] / $17$
Siano x, y e z numeri interi.
$x^2-x-8=y^2$
$x^2-x-(8+y^2)=0$
$x=\large \frac{1 \pm \sqrt{33+4y^2}}{2}$
perché x sia intero deve essere 33+4y² un quadrato perfetto
$33+4y^2=z^2$
$z^2-4y^2=33$
se y² è un quadrato perfetto anche 4y² lo è.
Vediamo anche che per y>8
$(2y+1)^2-(2y)^2>33$
per cui le soluzioni vanno ricercate per y compreso tra 1 e 8.
$\{ y=2 \\ y=8 \. \to \{ x^2=16 \\ x^2=81$
$x^2-x-8=y^2$
$x^2-x-(8+y^2)=0$
$x=\large \frac{1 \pm \sqrt{33+4y^2}}{2}$
perché x sia intero deve essere 33+4y² un quadrato perfetto
$33+4y^2=z^2$
$z^2-4y^2=33$
se y² è un quadrato perfetto anche 4y² lo è.
Vediamo anche che per y>8
$(2y+1)^2-(2y)^2>33$
per cui le soluzioni vanno ricercate per y compreso tra 1 e 8.
$\{ y=2 \\ y=8 \. \to \{ x^2=16 \\ x^2=81$
[Sergio] / $17$
Giusto!
La mia soluzione coincide con quella di quello fino al punto
$\displaystyle z^2-4y^2=33$
Io a questo punto ho scomposto $\displaystyle (z-2y)(z+2y)=3\cdot11=1\cdot33$ e i due fattori a primo membro devono valere 1 e 33 o 3 e 11(poichè sono ambedue interi per i termini del problema). Questo genera questa sequela di sistemi:
$\{ z-2y=1 \\ z+2y=33 \.$
$\{ z-2y=3 \\ z+2y=11 \.$
$\{ z-2y=33 \\ z+2y=1 \.$
$\{ z-2y=11 \\ z+2y=3 \.$
ciascuno dei quali dà una soluzione diversa. Gli ultimi due pero danno soluzioni con y negativo (da scartare per i termini del problema).
Quindi vanno bene le prime due che danno (z=17, y=8, x=9) e (z=7, y=2, x=4)
Altri metodi?
Ciao a tutti
Zerinf
La mia soluzione coincide con quella di quello fino al punto
$\displaystyle z^2-4y^2=33$
Io a questo punto ho scomposto $\displaystyle (z-2y)(z+2y)=3\cdot11=1\cdot33$ e i due fattori a primo membro devono valere 1 e 33 o 3 e 11(poichè sono ambedue interi per i termini del problema). Questo genera questa sequela di sistemi:
$\{ z-2y=1 \\ z+2y=33 \.$
$\{ z-2y=3 \\ z+2y=11 \.$
$\{ z-2y=33 \\ z+2y=1 \.$
$\{ z-2y=11 \\ z+2y=3 \.$
ciascuno dei quali dà una soluzione diversa. Gli ultimi due pero danno soluzioni con y negativo (da scartare per i termini del problema).
Quindi vanno bene le prime due che danno (z=17, y=8, x=9) e (z=7, y=2, x=4)
Altri metodi?
Ciao a tutti
Zerinf
Lo scopo principale di una dichiarazione DATA è quello di dare dei nomi alle costanti; anziché inserire ogni volta 3.141592653589793 come valore di $\pi$, con una dichiarazione DATA si può assegnare tale valore alla variabile PI che può essere poi usata per indicare la costante. Ciò rende anche più semplice modificare il programma, qualora il valore di $\pi$ dovesse cambiare.
-Da un vecchio manuale FORTRAN della Xerox
-Da un vecchio manuale FORTRAN della Xerox
Se qualcuno conosce i numeri triangolari Tn sa che il numero Tn è formato da n(n+1)/2 legionari, quindi potrebbe ragionare così:
Il manipolo e formato da x file di x legionari ciascuna, dunque quando cade la prima in tutto rimangono (x-1)x legionari, ovvero, ponendo (x-1)=n, rimangono n(n+1) legionari.
Ma n(n+1) = 2Tn e due numeri triangolari formano un quadrato solo se essi sono consecutivi:
T(n-1) + Tn = n^2
Opportunamente muoiono altri 8 legionari per cui è istintivo pensare a n=8, quindi uno dei T8 diventa T7 e:
n(n+1) - 8 = T7 + T8 = 8^2
(x-1)x - 8 = n(n+1) - 8 = 8^2
x^2 - x - 8 = (x-1)x - 8 = 8^2
da cui ricaviamo x=9 e i legionari erano 81.
Il manipolo e formato da x file di x legionari ciascuna, dunque quando cade la prima in tutto rimangono (x-1)x legionari, ovvero, ponendo (x-1)=n, rimangono n(n+1) legionari.
Ma n(n+1) = 2Tn e due numeri triangolari formano un quadrato solo se essi sono consecutivi:
T(n-1) + Tn = n^2
Opportunamente muoiono altri 8 legionari per cui è istintivo pensare a n=8, quindi uno dei T8 diventa T7 e:
n(n+1) - 8 = T7 + T8 = 8^2
(x-1)x - 8 = n(n+1) - 8 = 8^2
x^2 - x - 8 = (x-1)x - 8 = 8^2
da cui ricaviamo x=9 e i legionari erano 81.
Re: Le noccioline
Riesumare vecchi topic oramai è la mia passione 
Sapendo che
$\displaystyle x+y+z=0$
e
$\displaystyle x^2+y^2+z^2=14$,
quanto fa
$\displaystyle x^4+y^4+z^4=?$
Bye!
P.S. Come faccio a fare il comando \boxed sul forum? E' quello necessario per mettere un equazione in un "rettangolo"... spero di essermi spiegato
Sapendo che
$\displaystyle x+y+z=0$
e
$\displaystyle x^2+y^2+z^2=14$,
quanto fa
$\displaystyle x^4+y^4+z^4=?$
Bye!
P.S. Come faccio a fare il comando \boxed sul forum? E' quello necessario per mettere un equazione in un "rettangolo"... spero di essermi spiegato
Lo scopo principale di una dichiarazione DATA è quello di dare dei nomi alle costanti; anziché inserire ogni volta 3.141592653589793 come valore di $\pi$, con una dichiarazione DATA si può assegnare tale valore alla variabile PI che può essere poi usata per indicare la costante. Ciò rende anche più semplice modificare il programma, qualora il valore di $\pi$ dovesse cambiare.
-Da un vecchio manuale FORTRAN della Xerox
-Da un vecchio manuale FORTRAN della Xerox
Re: Le noccioline
Forse potresti utilizzare un'immagine:
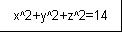
_________________
$\text { }$ciao ciao
ciao
E' la somma che fa il totale (Totò)
$\text { }$ciao
E' la somma che fa il totale (Totò)
Re: Le noccioline
Direi che $\displaystyle x^4+y^4+z^4=98$0-§ ha scritto:Sapendo che
$\displaystyle x+y+z=0$
e
$\displaystyle x^2+y^2+z^2=14$,
quanto fa
$\displaystyle x^4+y^4+z^4=?$
(x = 1 , y = 2 , z = -3)
ciao
Franco
ENGINEER
noun. (en-juh-neer)
someone who does precision guesswork based on unreliable data provided by those of questionable knowledge.
See also wizard, magician
ENGINEER
noun. (en-juh-neer)
someone who does precision guesswork based on unreliable data provided by those of questionable knowledge.
See also wizard, magician
Re: Le noccioline
A parte tutte le simmetrie possibili, includerei anche il caso:
x=-2; y=-1; z=3
x=-2; y=-1; z=3
_________________
$\text { }$ciao ciao
ciao
E' la somma che fa il totale (Totò)
$\text { }$ciao
E' la somma che fa il totale (Totò)
Re: Le noccioline
Ora naturalmente vogliamo sapere come è stato ottenuto il risultato 
P.S. Quelle soluzioni non importano, ricordate che in questo sistema $x,y,z \in \mathbb R$ quindi esiste un'infinità di possibili soluzioni
P.S. Quelle soluzioni non importano, ricordate che in questo sistema $x,y,z \in \mathbb R$ quindi esiste un'infinità di possibili soluzioni
Lo scopo principale di una dichiarazione DATA è quello di dare dei nomi alle costanti; anziché inserire ogni volta 3.141592653589793 come valore di $\pi$, con una dichiarazione DATA si può assegnare tale valore alla variabile PI che può essere poi usata per indicare la costante. Ciò rende anche più semplice modificare il programma, qualora il valore di $\pi$ dovesse cambiare.
-Da un vecchio manuale FORTRAN della Xerox
-Da un vecchio manuale FORTRAN della Xerox
Re: Le noccioline
Anche qui poca gloria:
che 14 fosse scomponibile nella somma di 3 quadrati ($1^2+2^2+3^2$) era abbastanza immediato, non restava che giocare un attimo coi segni per azzerare la somma delle basi.
Naturalmente non è e non voleva essere una soluzione generale; provo a ragionarci su.
ciao
che 14 fosse scomponibile nella somma di 3 quadrati ($1^2+2^2+3^2$) era abbastanza immediato, non restava che giocare un attimo coi segni per azzerare la somma delle basi.
Naturalmente non è e non voleva essere una soluzione generale; provo a ragionarci su.
ciao
Franco
ENGINEER
noun. (en-juh-neer)
someone who does precision guesswork based on unreliable data provided by those of questionable knowledge.
See also wizard, magician
ENGINEER
noun. (en-juh-neer)
someone who does precision guesswork based on unreliable data provided by those of questionable knowledge.
See also wizard, magician
-
Admin
- Amministratore del sito

- Messaggi: 870
- Iscritto il: mer apr 20, 2005 3:47 pm
- Località: Benevento
Re: Le noccioline
Ciao,
mi sembra basti fare qualche sostituzione.
$x+y+z = 0\qquad\Rightarrow\qquad x=-y-z$
Sostituiamo nella seconda:
$x^2+y^2+z^2=14\qquad\Rightarrow\qquad (-y-z)^2+y^2+z^2-14=0\qquad\Rightarrow\qquad y^2+z^2+yz-7=0$
Risolvendo secondo $y$ si ottiene:
$y={\large\frac{-z\pm \sqrt{-3z^2+28}}{2}}$
ossia
$\{ y_1={\large\frac{-z\/+\/\sqrt{-3z^2\/+\/28}}{2}} \\ y_2={\large\frac{-z\/-\/\sqrt{-3z^2\/+\/28}}{2}}$
Andiamo ora a ricavare i valori $x_1$ e $x_2$, sostituendo, rispettivamente, $y_1$ e $y_2$:
$\{ x_1=\/-\/\({\large\frac{-z\/+\/\sqrt{-3z^2\/+\/28}}{2}}\)\/-\/z\qquad\Rightarrow\qquad {\large\frac{-z\/-\/\sqrt{-3z^2\/+\/28}}{2}} \\x_2=\/-\/\({\large\frac{-z\/-\/\sqrt{-3z^2\/+\/28}}{2}}\)\/-\/z\qquad\Rightarrow\qquad {\large\frac{-z\/+\/\sqrt{-3z^2\/+\/28}}{2}}$
Ora andiamo a sostituire le coppie $(x_1, y_1)$ e $(x_2, y_2)$ trovate, nell'espressione $x^4+y^4+z^4$.
Prima di sostituire, si nota che $x_1=y_2$ e $x_2=y_1$; ciò significa che ${x_1}^4+{y_1}^4+z^4\/=\/{x_2}^4+{y_2}^4+z^4$
Per cui sostituiamo solo la coppia $(x_1, y_1)$. Si ottiene:
$x^4+y^4+z^4\/=\/\({\large\frac{-z\/-\/\sqrt{-3z^2\/+\/28}}{2}}\)^4\/+\/\({\large\frac{-z\/+\/\sqrt{-3z^2\/+\/28}}{2}}\)^4\/+\/z^4$
Sviluppando le potenze di binomio e semplificando si ottiene:
$x^4+y^4+z^4\/=\/98$
SE&O
Ciao
Admin
mi sembra basti fare qualche sostituzione.
$x+y+z = 0\qquad\Rightarrow\qquad x=-y-z$
Sostituiamo nella seconda:
$x^2+y^2+z^2=14\qquad\Rightarrow\qquad (-y-z)^2+y^2+z^2-14=0\qquad\Rightarrow\qquad y^2+z^2+yz-7=0$
Risolvendo secondo $y$ si ottiene:
$y={\large\frac{-z\pm \sqrt{-3z^2+28}}{2}}$
ossia
$\{ y_1={\large\frac{-z\/+\/\sqrt{-3z^2\/+\/28}}{2}} \\ y_2={\large\frac{-z\/-\/\sqrt{-3z^2\/+\/28}}{2}}$
Andiamo ora a ricavare i valori $x_1$ e $x_2$, sostituendo, rispettivamente, $y_1$ e $y_2$:
$\{ x_1=\/-\/\({\large\frac{-z\/+\/\sqrt{-3z^2\/+\/28}}{2}}\)\/-\/z\qquad\Rightarrow\qquad {\large\frac{-z\/-\/\sqrt{-3z^2\/+\/28}}{2}} \\x_2=\/-\/\({\large\frac{-z\/-\/\sqrt{-3z^2\/+\/28}}{2}}\)\/-\/z\qquad\Rightarrow\qquad {\large\frac{-z\/+\/\sqrt{-3z^2\/+\/28}}{2}}$
Ora andiamo a sostituire le coppie $(x_1, y_1)$ e $(x_2, y_2)$ trovate, nell'espressione $x^4+y^4+z^4$.
Prima di sostituire, si nota che $x_1=y_2$ e $x_2=y_1$; ciò significa che ${x_1}^4+{y_1}^4+z^4\/=\/{x_2}^4+{y_2}^4+z^4$
Per cui sostituiamo solo la coppia $(x_1, y_1)$. Si ottiene:
$x^4+y^4+z^4\/=\/\({\large\frac{-z\/-\/\sqrt{-3z^2\/+\/28}}{2}}\)^4\/+\/\({\large\frac{-z\/+\/\sqrt{-3z^2\/+\/28}}{2}}\)^4\/+\/z^4$
Sviluppando le potenze di binomio e semplificando si ottiene:
$x^4+y^4+z^4\/=\/98$
SE&O
Ciao
Admin
Pietro Vitelli (Amministratore del Forum)
"Un matematico è una macchina che converte caffè in teoremi" Paul Erdös
www.pvitelli.net
"Un matematico è una macchina che converte caffè in teoremi" Paul Erdös
www.pvitelli.net
Re: Le noccioline
Penso di poter postare ora la risposta rapida 
Sapendo che
$\displaystyle x+y+z=0$ (A)
e
$\displaystyle x^2+y^2+z^2=14$ (B)
elevando al quadrato entrambi i membri di (A) e considerando la condizione (B) si trova che
$\displaystyle 0^2=(x+y+z)^2=x^2+y^2+z^2+2(xy+xz+yz)\\=14+2(xy+xz+yz)$
pertanto
$\displaystyle xy+xz+yz=-7$. (1)
Ora elevando al quadrato entrambi i membri di (1) si trova
$\displaystyle 49=(xy+xz+yz)^2=x^2 y^2+x^2 z^2+y^2 z^2 + 2x^2 yz+2xy^2 z+2xyz^2\\=x^2 y^2+x^2 z^2+y^2 z^2 + 2xyz(x+y+z)=x^2 y^2+x^2 z^2+y^2 z^2$. (2)
Ultimo atto:elevando al quadrato entrambi i membri di (B) e usando quanto appena visto in (2)
$\displaystyle 14^2=(x^2+y^2+z^2)^2=x^4 + y^4 + z^4 + 2x^2 y^2 +2x^2 z^2 +2y^2 z^2\\=x^4 + y^4 + z^4 +2\cdot 49$
sicchè
$\displaystyle x^4 + y^4 +z^4= 98$.
Bello, nevvero?
Buonanotte a tutti
ZerInf
Sapendo che
$\displaystyle x+y+z=0$ (A)
e
$\displaystyle x^2+y^2+z^2=14$ (B)
elevando al quadrato entrambi i membri di (A) e considerando la condizione (B) si trova che
$\displaystyle 0^2=(x+y+z)^2=x^2+y^2+z^2+2(xy+xz+yz)\\=14+2(xy+xz+yz)$
pertanto
$\displaystyle xy+xz+yz=-7$. (1)
Ora elevando al quadrato entrambi i membri di (1) si trova
$\displaystyle 49=(xy+xz+yz)^2=x^2 y^2+x^2 z^2+y^2 z^2 + 2x^2 yz+2xy^2 z+2xyz^2\\=x^2 y^2+x^2 z^2+y^2 z^2 + 2xyz(x+y+z)=x^2 y^2+x^2 z^2+y^2 z^2$. (2)
Ultimo atto:elevando al quadrato entrambi i membri di (B) e usando quanto appena visto in (2)
$\displaystyle 14^2=(x^2+y^2+z^2)^2=x^4 + y^4 + z^4 + 2x^2 y^2 +2x^2 z^2 +2y^2 z^2\\=x^4 + y^4 + z^4 +2\cdot 49$
sicchè
$\displaystyle x^4 + y^4 +z^4= 98$.
Bello, nevvero?
Buonanotte a tutti
ZerInf
Lo scopo principale di una dichiarazione DATA è quello di dare dei nomi alle costanti; anziché inserire ogni volta 3.141592653589793 come valore di $\pi$, con una dichiarazione DATA si può assegnare tale valore alla variabile PI che può essere poi usata per indicare la costante. Ciò rende anche più semplice modificare il programma, qualora il valore di $\pi$ dovesse cambiare.
-Da un vecchio manuale FORTRAN della Xerox
-Da un vecchio manuale FORTRAN della Xerox
Re: Le noccioline
Si, beddissimo fu
_________________
$\text { }$ciao ciao
ciao
E' la somma che fa il totale (Totò)
$\text { }$ciao
E' la somma che fa il totale (Totò)





