Buon pomeriggio, Tania

Ho trovato uno scampolo di tempo nella pausa del pranzo e ho messo mano al tuo quesito.
Ti riporto la mia risoluzione, la scrivo così come l'ho scarabocchiata

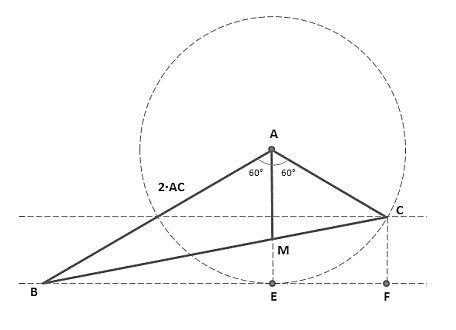
- Tesspi.jpg (12.66 KiB) Visto 3224 volte
Per il noto
teorema della bisettrice, se $\small AB$ è il doppio di $\small AC$, allora $\small BM$ è il doppio di $\small MC$, di conseguenza pure $\small BE$ è il doppio di $\small EF$.
Vediamo in che modo può esserci utile questo fatto.
Ragionando sui triangoli rettangoli simili con le ipotenuse su $\small BC$:
$\small BE\, :\, EM\, =\, BF\, :\, CF$
cioè:
2·$\small EF$ : ($\small AC$-2019) = 3·$\small EF$ : $\frac{AC}{2}$
da cui si ottiene:
$\small AC \, = \,{\large \frac{3\cdot 2019}{2}}\, = \, {\large \frac{9\cdot 673}{2}}$.
Ora, poiché:
$\small BF \,=\, 3\cdot EF\;\;$ (lo abbiamo già visto)
e:
${\small EF = AC}\cdot {\large \frac{\sqrt{3}}{2}}\;\; $ (è l'altezza del triangolo equilatero di lato $\, \small AC$,
la formula è nota)
abbiamo subito:
${\small BF = AC\cdot 3}\cdot {\large \frac{\sqrt{3}}{2}} $.
Dunque, grazie al caro
Pitagora:
${\small BC = \sqrt{BF^2 + CF^2}} = \sqrt{\left({\small AC\cdot 3}\cdot {\large \frac{\sqrt{3}}{2}}\right)^2 + \left({\large \frac{AC}{2}}\right)^2} = {\large \frac{AC}{2}}\cdot \sqrt{\small 9\cdot 3+1} = {\small AC}\cdot \sqrt{7} = {\large \frac{9·673}{2}}\cdot \sqrt{7} \; ≈ \; 8013\,$ metri.
Ho lasciato le approssimazioni all'ultimo passaggio: meno si approssima, in geometria, meglio è.
Cosa dici, Tania, ora riesci a orientarti nella tua foresta?


