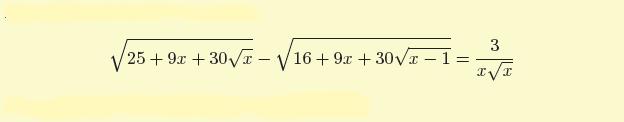
Equazione
Moderatori: Gianfranco, Bruno
Questo forum è una sezione del PORTALE DI BASE CINQUE
Re: Equazione
Vale anche tirare ad indovinare e poi scoprire di aver fatto centro al primo colpo? 
ciao
ciao
Franco
ENGINEER
noun. (en-juh-neer)
someone who does precision guesswork based on unreliable data provided by those of questionable knowledge.
See also wizard, magician
ENGINEER
noun. (en-juh-neer)
someone who does precision guesswork based on unreliable data provided by those of questionable knowledge.
See also wizard, magician
Re: Equazione
Beh a lune di naso direi che la soluzione sia x=1 che se non ho sbagliato i conti è accettabile dentro il C.E. per le realtà delle radici cioè X>=1 con l'esclusione dell'intervallo compreso tra le soluzioni dell'equazione associata alla disequazione che da la realtà della seconda "grossa radice" a sx dell'uguale.
Ah, se i portieri avessero sulla maglia: $|e^{-i\pi}|$...
Pongo $y = x^{2}$ quindi $y=\frac {x^{2}}{pongo}$
[tratto da un compito in classe di uno studente di prima superiore]
Il vero gnomone aureo: http://thumbs.dreamstime.com/z/gnomo-de ... 526933.jpg
Pongo $y = x^{2}$ quindi $y=\frac {x^{2}}{pongo}$
[tratto da un compito in classe di uno studente di prima superiore]
Il vero gnomone aureo: http://thumbs.dreamstime.com/z/gnomo-de ... 526933.jpg
Re: Equazione
Guardando l'equazione, dai coefficienti al primo membro ho notato che
$25+9x+30\sqr{x}=(3\sqr{x}+5)^2$ e $16+9x+30\sqr{x-1}=(3\sqr{x-1}+5)^2$
da cui l'equazione diviene
$|3\sqr{x}+5)|-|3\sqr{x-1}+5|=\frac{3}{x\sqr{x}}$.
Per la realtà delle radici deve essere $x\ge 1$ per cui entrambi i termini entro i valori asssoluti sono positivi e l'equazione diviene
$\sqr{x}-\sqr{x-1}=\frac{1}{x\sqr{x}}$.
Riducendo e quadrando si perviene a
$x^3-2x^2+1=0$
che ammette le soluzioni
$x=1$ $x=\frac{1+\sqr{5}}{2}$ $x=\frac{1-\sqr{5}}{2}$
Dalla verifica, indispensabile per equazioni irrazionali, si ricava che solo i primi due valori sono accettabili.
$25+9x+30\sqr{x}=(3\sqr{x}+5)^2$ e $16+9x+30\sqr{x-1}=(3\sqr{x-1}+5)^2$
da cui l'equazione diviene
$|3\sqr{x}+5)|-|3\sqr{x-1}+5|=\frac{3}{x\sqr{x}}$.
Per la realtà delle radici deve essere $x\ge 1$ per cui entrambi i termini entro i valori asssoluti sono positivi e l'equazione diviene
$\sqr{x}-\sqr{x-1}=\frac{1}{x\sqr{x}}$.
Riducendo e quadrando si perviene a
$x^3-2x^2+1=0$
che ammette le soluzioni
$x=1$ $x=\frac{1+\sqr{5}}{2}$ $x=\frac{1-\sqr{5}}{2}$
Dalla verifica, indispensabile per equazioni irrazionali, si ricava che solo i primi due valori sono accettabili.
Vittorio
Re: Equazione
Ottima soluzione .Io mi ero affidato alla formula del radicale quadratico doppio,ma così è più veloce.Quanto alla verifica diretta ,credo che ci si possa limitare alle prime due radici dato che la terza è negativa e non soddisfa la condizione x>=1
Ciao
Ciao




