http://imageshack.us/photo/my-images/233/figxx.png/
Una curiosa generalizzazione della nota regola di Ruffini.Presumo sia già nota.Sia come sia,eccola.
Si voglia eseguire la divisione:
$\large (x^4+5x^3+2x^2-15):(x^2-2x+3)$
A) I due polinomi devono essere ordinati secondo le potenze decrescenti della lettera rispetto a cui si esegue la divisione,supplendo con qualche zero le eventuali potenze mancanti.Inoltre il primo coefficiente del divisore deve essere 1 .Se non lo è occorre dividere il divisore per il suddetto coefficiente,ricordando però che alla fine il quoziente ottenuto va diviso per quel coefficiente.
B) Preparate una griglia di (m+2)x(n+2) caselle ,dove m=grado dividendo,n=grado divisore ( nel nostro caso 6x4=24 caselle).
C) Nella prima riga, a partire dalla seconda casella,mettete i coeff. del dividendo
D1) Nella prima colonna ,a partire dalla seconda casella,mettete i coeff. del divisore cambiati di segno , a partire dall'ultimo e tranne il primo coeff. ( che è =1).
D2)"Abbassate " il primo coeff. del dividendo nell'ultima riga.Vedi fig.A
E) Moltiplicate il coeff."abbassato" (1,nel nostro caso) per i coeff. del divisore ed i prodotti ottenuti scriveteli in diagonale nelle righe immediatamente superiori.
F) Sommate i valori scritti nella terza colonna,ottenendo 7 nel nostro caso.Vedi fig.B
G) Ripetete per il 7 così ottenuto l'operazione e sommate i valori della quarta colonna ,ottenendo 13 nel nostro caso.
H) Ripetete le operazioni fino a quando non compare un valore sotto l'ultimo coeff.del dividendo ( -39,nel nostro caso).Vedi fig.C
Conclusione.
Il polinomio quoziente Q(x),che deve essere di secondo grado ed ha quindi 3 coeff.,ha come coefficienti i primi 3 valori dell'ultima riga.I restanti due valori sono i coeff. del resto R(x) che è di primo grado.Pertanto avremo:
$Q(x)=x^2+7x+13;R(x)=5x-54$
Divisione di polinomi
Moderatori: Gianfranco, Bruno
Questo forum è una sezione del PORTALE DI BASE CINQUE
Divisione di polinomi
Ultima modifica di karl il gio nov 03, 2011 8:36 pm, modificato 1 volta in totale.
Re: Divisione di polinomi
Questo tipo di divisione l'ho fatta sempre come una normale divisione (man, mano che si procede, si divide sempre il primo termine del dividendo con il primo del divisore; poi si moltiplica il risultato per tutto il divisore e lo si sottrae al dividendo, procedendo similmente finché il primo termine del divisore non abbia un grado inferiore a quello del primo termine del dividendo; prima di procedere, i due polinomi vengono ordinati come hai già detto sopra):
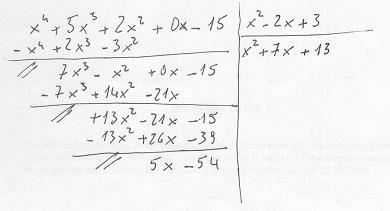
altra:
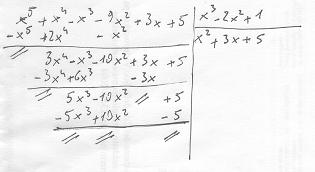
altra:
_________________
$\text { }$ciao ciao
ciao
E' la somma che fa il totale (Totò)
$\text { }$ciao
E' la somma che fa il totale (Totò)
Re: Divisione di polinomi
Il metodo esposto da Pasquale è quello correntemente adoperato in algebra elementare.Io ho solo voluto
indicare una... simpatica estensione della familiare regola di Ruffini che non vuole assolutamente sostituire
quella usata da sempre... Insomma prendete la cosa come un divertente diversivo
indicare una... simpatica estensione della familiare regola di Ruffini che non vuole assolutamente sostituire
quella usata da sempre... Insomma prendete la cosa come un divertente diversivo
Re: Divisione di polinomi
Mi sembra davvero carinissima l'estensione della regola di Ruffini; non conoscevo tale estensione, ma le tue indicazioni, inerenti a ogni passaggio da seguire, sono molto chiare e ben dettagliate. Dove hai trovato tale simpatica curiosità?
Grazie
Grazie

"L'essenza della matematica è la libertà" (Georg Cantor)
Re: Divisione di polinomi
Lo schema è del prof.Giovanni Artico ( che scherzosamente ama farsi chiamare "polarprof" !)
Lo puoi trovare sul sito CENTRO RICERCHE DIDATTICHE U.MORIN
Ti passo il link corrispondente ( sperando che funzioni...).Saluti
$[tex]$http://www.centromorin.it/aspnuke207/ar ... d=5&page=2[/tex]
Lo puoi trovare sul sito CENTRO RICERCHE DIDATTICHE U.MORIN
Ti passo il link corrispondente ( sperando che funzioni...).Saluti
$[tex]$http://www.centromorin.it/aspnuke207/ar ... d=5&page=2[/tex]
Re: Divisione di polinomi
Grazie, Karl...
Ho un dubbio: perché nello schema di polarprof si legge: "lasciando per il resto tante caselle quante il grado del divisore meno 1"?
A me sembra che sia nel tuo esempio, sia nell'esempio dello stesso polarprof, risultino per il resto tante caselle quante il grado del divisore...
Ho provato a svolgere un esercizio proposto nel sito dell'unibo e le caselle per il resto mi risultano tante quante il grado del divisore:
http://www.dm.unibo.it/~cerri/OFA/Giorn ... linomi.pdf" target="_blank
Edito per aggiungere che, forse, il polarprof intende dire che per il resto risultano tante caselle quanti sono tutti i monomi meno 1 (per monomi intendo compresi gli zeri) che compongono il divisore... È così?
Ho un dubbio: perché nello schema di polarprof si legge: "lasciando per il resto tante caselle quante il grado del divisore meno 1"?
A me sembra che sia nel tuo esempio, sia nell'esempio dello stesso polarprof, risultino per il resto tante caselle quante il grado del divisore...
Ho provato a svolgere un esercizio proposto nel sito dell'unibo e le caselle per il resto mi risultano tante quante il grado del divisore:
http://www.dm.unibo.it/~cerri/OFA/Giorn ... linomi.pdf" target="_blank
Edito per aggiungere che, forse, il polarprof intende dire che per il resto risultano tante caselle quanti sono tutti i monomi meno 1 (per monomi intendo compresi gli zeri) che compongono il divisore... È così?
- Allegati
-
- divisione_polinomi.gif (17.46 KiB) Visto 6342 volte

"L'essenza della matematica è la libertà" (Georg Cantor)
Re: Divisione di polinomi
Credo che nei commenti di polarprof ci sia qualche refuso.Va bene come abbiamo fatto noi...
Complimenti per il disegno !
Complimenti per il disegno !
Re: Divisione di polinomi
Grazie, Karl.
Forse per deformazione professionale, sovente a me interessa cercare di capire le motivazioni dei refusi miei, o altrui...
Forse per deformazione professionale, sovente a me interessa cercare di capire le motivazioni dei refusi miei, o altrui...

"L'essenza della matematica è la libertà" (Georg Cantor)



