...
Pufff...
Normalmente mi occupo delle questioni solo quando penso di poter scrivere
abbastanza in fretta la risposta, anche e soprattutto perché il tempo manca.
Peraltro, non sono sicuramente abile come Panurgo a impostare formule, a
tracciarte disegni e, ovviamente, a elaborare agili risoluzioni, per cui...
Tuttavia non sono riuscito a sorvolare sull'interessante questione qui proposta
(come invece faccio spesso) e ho provato a buttare giù qualche calcolo.
Ignoro la soluzione e temo di aver perso qualche simbolo strada facendo,
quindi mi scuso per l'inevitabile improvvisazione di questo mio post.
Ma andiamo avanti...
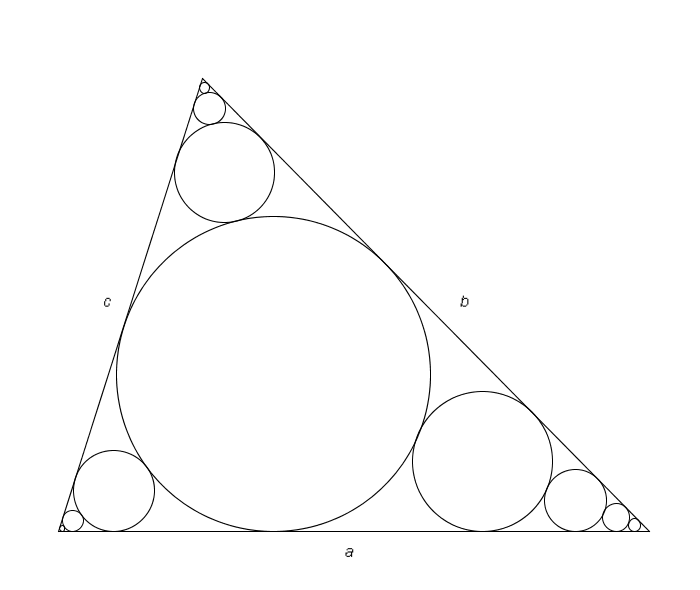
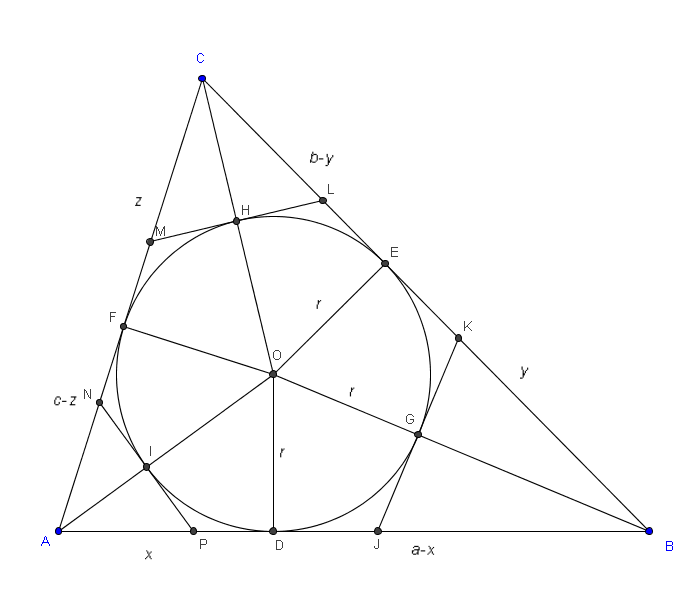
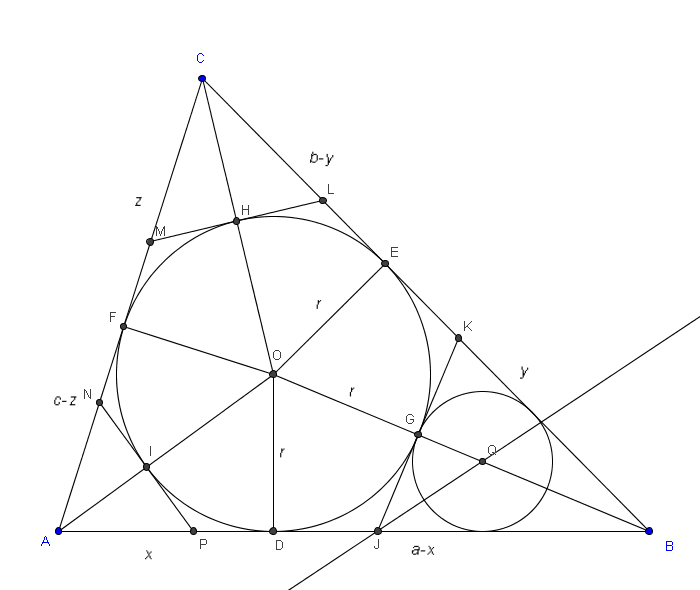
Di seguito riproduco un disegno fatto in fretta con Excel (?!?), con il quale
però spero lo stesso di chiarire i miei passaggi:

I dati del problema sono i lati e quindi potrei già considerare noti anche
il raggio del cerchio inscritto:
$\displaystyle r_0 = \frac {\sqr {p(p-a)(p-b)(p-c)}}{p}$
e i seguenti seni (Briggs):
$\displaystyle sen \frac \alpha 2 = \sqr {\frac {(p-b)(p-c)}{bc}} \\ sen \frac \beta 2 = \sqr {\frac {(p-a)(p-c)}{ac}} \\ sen \frac \gamma 2 = \sqr {\frac {(p-a)(p-b)}{ab}} \, ,$
essendo
p il semiperimetro.
La figura rappresenta un solo vertice del triangolo, dal momento che le
considerazioni che farò su questa parte potranno essere applicate anche
agli altri due vertici.
I due raggi messi in evidenza sono perpendicolari al lato
a, poiché condividono
con tale lato i punti di tangenza delle rispettive circonferenze.
Posso dire, allora, che:
$\displaystyle r_0-r_1 = (r_0+r_1)sen \frac \gamma 2$
ossia:
$\displaystyle r_1 = r_0 \left( \frac {1-sen \frac \gamma 2}{1+sen \frac \gamma 2} \right) = r_0 \cdot t_\gamma$
utilizzando $\displaystyle t_\gamma$ per brevità.
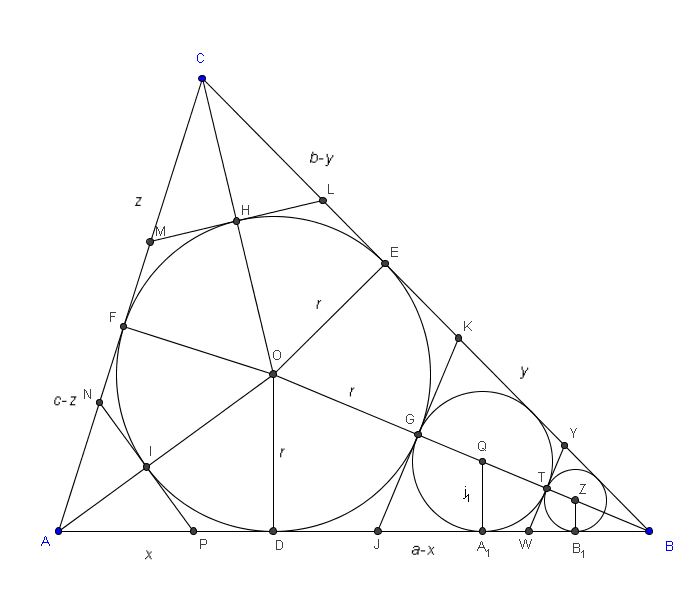
Per lo stesso principio, d'altra parte, riguardo alle circonferenze più piccole
successive (che dovremo immaginare), posso anche dire:
$\displaystyle r_2 = r_1 \cdot t_\gamma \\ r_3 = r_2 \cdot t_\gamma \\ r_4 = r_3 \cdot t_\gamma \,\,\, \cdots$
e cioè:
$\displaystyle r_2 = r_0 \cdot t_\gamma^2 \\ r_3 = r_0 \cdot t_\gamma^3 \\ r_4 = r_0 \cdot t_\gamma^4 \,\,\, \cdots$
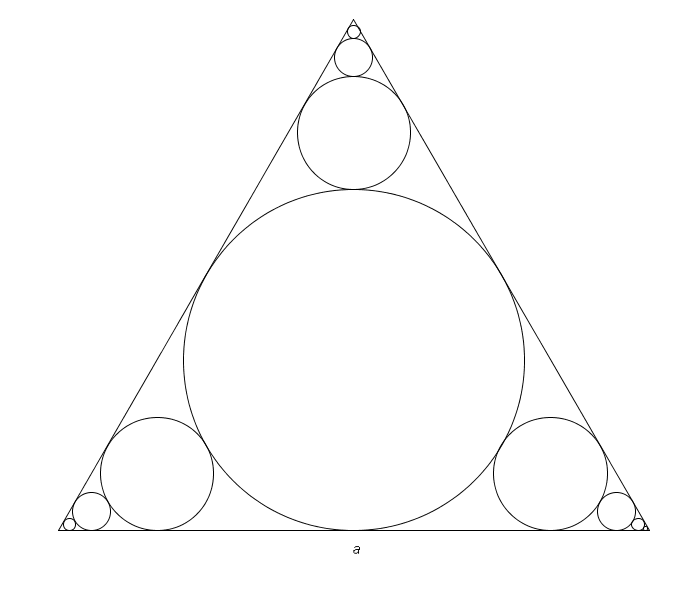
La somma delle aree degli infiniti cerchi compresi fra il cerchio inscritto nel
triangolo e il vertice, pertanto, è:
$\displaystyle \pi \cdot r_0^2 \cdot \left[(t_\gamma^2)+(t_\gamma^2)^2+(t_\gamma^2)^3+...\right] = \pi \cdot r_0^2 \cdot \frac {t_\gamma^2}{1-t_\gamma^2} \,\,\, ,$
trattandosi di una progressione geometrica senza l'unità iniziale ed essendo,
inoltre, $\displaystyle \, t_\gamma^2 < 1 \,$ per $\displaystyle \, 0 <\gamma< 180^o$ .
Questo valore, naturalmente, non comprende l'area del cerchio con raggio $\displaystyle r_0$.
Analogamente, trovo la stessa somma dei cerchi infiniti relativi agli altri due
vertici:
- vertice in $\displaystyle \beta$: $\displaystyle \,\,\, \pi \cdot r_0^2 \cdot \frac {t_\beta^2}{1-t_\beta^2} \,\, ,$
- vertice in $\displaystyle \alpha$: $\displaystyle \,\,\, \pi \cdot r_0^2 \cdot \frac {t_\alpha^2}{1-t_\alpha^2} \,\, .$
L'area totale, allora, è data dalla somma delle tre aree appena trovate, a cui
bisogna aggiungere quella del cerchio inscritto:
$\displaystyle \pi \cdot r_0^2 \cdot \left (1+\frac {t_\alpha^2}{1-t_\alpha^2}+\frac {t_\beta^2}{1-t_\beta^2}+\frac {t_\gamma^2}{1-t_\gamma^2} \right )$
A questo punto, volendo, potrei fare tutte le sostituzioni per esprimere il risultato
in funzione dei lati, ma sono ormai alla frutta... perciò rinvio alle formule iniziali

PS - Se il triangolo fosse equilatero e con lato unitario, si avrebbe:
$\displaystyle \frac \alpha 2 = \frac \beta 2 = \frac \gamma 2 = 30^o$
con seno uguale a 1/2. Quindi:
$\displaystyle t = \frac {1-\frac 1 2}{1+\frac 1 2} = \frac 1 3$
mentre:
$\displaystyle \frac {t^2}{1-t^2} = \frac 1 8 \\ r_0 = 1 \cdot \frac {\sqr 3}{6} \,\, .$
L'area di tutti cerchi, in questo caso, sarebbe:
$\displaystyle \pi \cdot \frac 1 {12} \cdot \left (1+3 \cdot\frac 1 8 \right ) = \pi \cdot \frac {11} {96}$
in accordo con il risultato di Archie.

Bruno
_____________________________________________________________________________
PS - Sistemato un po' l'italiano frettoloso, ora dovrebbe andare meglio. (9 gennaio 2006)