Cerchi e anelli
Moderatori: Gianfranco, Bruno
Questo forum è una sezione del PORTALE DI BASE CINQUE
Cerchi e anelli
Ciao a tutti,
mi sono dato da fare un po' con Geogebra ed ho elaborato questo problema:
Dato un cerchio, tracciare graficamente due anelli, uno interno e uno esterno al cerchio, tali che la somma delle loro aree corrisponda a quella del cerchio.
Ciao
mi sono dato da fare un po' con Geogebra ed ho elaborato questo problema:
Dato un cerchio, tracciare graficamente due anelli, uno interno e uno esterno al cerchio, tali che la somma delle loro aree corrisponda a quella del cerchio.
Ciao
[Sergio] / $17$
Re: Cerchi e anelli
Se ho capito bene si tratta di tracciare tre cerchi concentrici tali che l'area di quello centrale dato equivalga all'area della corona circolare delimitata dal cerchio interno e da quello esterno.
Vittorio
Re: Cerchi e anelli
Questa è una possibile interpretazione (non riesco però a vedere la soluzione che hai inserito, vedo solo un campo bianco), ma in realtà la mia intenzione era quella di trovare due cerchi concentrici all'interno di quello dato e due all'esterno tali per cui le aree delle due corone circolari sommate diano l'area del cerchio dato.
Vi metto una possibile soluzione per chiarire la cosa ($A_{blu} + A_{rossa} = A_{cerchionero}$)

Nota: L'area grigia è uguale all'area del cerchio nero, cioè la soluzione della tua interpretazione
Vi metto una possibile soluzione per chiarire la cosa ($A_{blu} + A_{rossa} = A_{cerchionero}$)
Nota: L'area grigia è uguale all'area del cerchio nero, cioè la soluzione della tua interpretazione
[Sergio] / $17$
Re: Cerchi e anelli
Non è chiaro quali siano i vincoli: l'altezza delle due corone circolari deve essere la stessa?... 
il panurgo
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
Re: Cerchi e anelli
Chiedo scusa ma non riuscivo ad inserire geogebra.
Costruisco la retta AB e traccio la circongerenza (nera) centro A e raggio AB. Su AB prendo un punto C a piacere e traccio la circonferenza (rossa) centro A e raggio AC.
La perpendicolare per A ad AB incontra la circonferenza nera in D. La parallela per D ad AB incontra la perpendicolare per C ad AB nel punto E. Traccio la circonferenza (blu) centro A e raggio AE.
L'area del cerchio nero equivale a quella della corona circolare delimitata dalle circonferenze rossa e blu.
Vittorio
Re: Cerchi e anelli
il testo recita:
Dato un cerchio, tracciare graficamente due anelli, uno interno e uno esterno al cerchio, tali che la somma delle loro aree corrisponda a quella del cerchio.
mi sembra che la soluzione proposta faccia riferimento non alla somma, ma alla differenza delle aree.
Non vi è peraltro nessun riferimento alla "concentricità" delle tre circonferenze.
Facendo per comodità riferimento alla situazione disegnata, e considerando l'asse orizzontale, si tratta di trovare per ogni valore di AC, il punto sul prolungamento del raggio (diciamo BE facendo scivolare giù il punto E) tale per cui la corona tra B e E sia equivalente al cerchio con raggio AC
Dato un cerchio, tracciare graficamente due anelli, uno interno e uno esterno al cerchio, tali che la somma delle loro aree corrisponda a quella del cerchio.
mi sembra che la soluzione proposta faccia riferimento non alla somma, ma alla differenza delle aree.
Non vi è peraltro nessun riferimento alla "concentricità" delle tre circonferenze.
Facendo per comodità riferimento alla situazione disegnata, e considerando l'asse orizzontale, si tratta di trovare per ogni valore di AC, il punto sul prolungamento del raggio (diciamo BE facendo scivolare giù il punto E) tale per cui la corona tra B e E sia equivalente al cerchio con raggio AC
Enrico
Re: Cerchi e anelli
Credo che per "anello", s' intenda proprio la corona circolare (o, almeno, io concordo pienamente con la risoluzione di Vittorio...)
La differenza tra l'area del cerchio blu e l'area del cerchio rosso corrisponde proprio alla somma delle aree delle due corone circolari...
La differenza tra l'area del cerchio blu e l'area del cerchio rosso corrisponde proprio alla somma delle aree delle due corone circolari...

"L'essenza della matematica è la libertà" (Georg Cantor)
Re: Cerchi e anelli
Ok, mi sono espresso male, chiedo scusa per l'uso di terminologia impropria.
Per anelli intendevo appunto corone circolari.
In ogni caso adesso abbiamo due problemi:
il primo è quello risolto da Vittorio:
Dato un cerchio, trovare graficamente due circonferenze, una interna e una esterna al cerchio, tali per cui l'area della corona circolare delimitata dalle due circonferenze sia pari a quella del cerchio dato
Ora che vedo la soluzione di Vittorio devo dire che è semplice ed elegante e risponde in pieno a questo problema.
il secondo è quello che intendevo proporre io:
Dato un cerchio, trovare graficamente 4 circonferenze, due interne e due esterne al cerchio, tali per cui la somma delle aree delle corone circolari delimitate rispettivamente dalle due corone interne e dalle due corone esterne sia pari all'area del cerchio dato
Direi che a partire dalla soluzione di Vittorio, con due semplici passaggi si risolve anche questo.
Il problema non pone alcun vincolo sulle circonferenze, ad eccezione delle aree delimitate e della loro posizione.
Dovendole trovare graficamente, penso che la soluzione sia più semplice se sono tutte concentriche.
Per anelli intendevo appunto corone circolari.
In ogni caso adesso abbiamo due problemi:
il primo è quello risolto da Vittorio:
Dato un cerchio, trovare graficamente due circonferenze, una interna e una esterna al cerchio, tali per cui l'area della corona circolare delimitata dalle due circonferenze sia pari a quella del cerchio dato
Ora che vedo la soluzione di Vittorio devo dire che è semplice ed elegante e risponde in pieno a questo problema.
il secondo è quello che intendevo proporre io:
Dato un cerchio, trovare graficamente 4 circonferenze, due interne e due esterne al cerchio, tali per cui la somma delle aree delle corone circolari delimitate rispettivamente dalle due corone interne e dalle due corone esterne sia pari all'area del cerchio dato
Direi che a partire dalla soluzione di Vittorio, con due semplici passaggi si risolve anche questo.
Il problema non pone alcun vincolo sulle circonferenze, ad eccezione delle aree delimitate e della loro posizione.
Dovendole trovare graficamente, penso che la soluzione sia più semplice se sono tutte concentriche.
[Sergio] / $17$
Re: Cerchi e anelli
da quel che dici, pare di capire che poni per la corona più piccola il vincolo che la sua circonferenza esterna sia inferiore alla circonferenza di base e per la corona maggiore si pretende che la circonferenza minore sia maggiore della data.
il solo fatto di essere "esterna" non implica di per sè nulla sulle dimensioni. Se poniamo il vincolo della concentricità, non solo è più semplice, ma il testo diventa univoco
il solo fatto di essere "esterna" non implica di per sè nulla sulle dimensioni. Se poniamo il vincolo della concentricità, non solo è più semplice, ma il testo diventa univoco
Enrico
Re: Cerchi e anelli
Mi pare che il problema dei vincoli sia più acuto che mai.
Preso un cerchio di raggio unitario (arbitrario), disegnamo due corone circolari, una di raggio esterno minore (ma arbitrario) e l'altra di raggio interno maggiore (e arbitrario) di quello del cerchio iniziale. Al variare (arbitrario) dell'altezza (arbitraria) di una delle corone circolari si osserva che vi è sempre, per l'altra corona circolare, un'altezza (e una sola, quindi non arbitraria) tale che il cerchio è equivalente alla somma delle due corone.
Dato il primo cerchio (arbitrario) abbiamo infinite corone di raggio esterno inferiore a quello del cerchio dato; dato il raggio esterno della prima corona abbiamo infinite altezze di detta corona; abbiamo inoltre infiniti segmenti maggiori del raggio del cerchio dato che possono fungere da raggio interno per la seconda corona circolare: finalmente, fissato anche questo raggio interno esiste una e una sola altezza per la seconda corona.
Che le corone siano concentriche o interne al cerchio dato è irrilevante (se non in quanto limita l'intervallo di raggi validi per la corona interna).
E' ovviamente possibile fare in modo che il raggio interno della corona esterna e il raggio esterno della corona interna siano uguali ottenendo una corona unica...
Preso un cerchio di raggio unitario (arbitrario), disegnamo due corone circolari, una di raggio esterno minore (ma arbitrario) e l'altra di raggio interno maggiore (e arbitrario) di quello del cerchio iniziale. Al variare (arbitrario) dell'altezza (arbitraria) di una delle corone circolari si osserva che vi è sempre, per l'altra corona circolare, un'altezza (e una sola, quindi non arbitraria) tale che il cerchio è equivalente alla somma delle due corone.
Dato il primo cerchio (arbitrario) abbiamo infinite corone di raggio esterno inferiore a quello del cerchio dato; dato il raggio esterno della prima corona abbiamo infinite altezze di detta corona; abbiamo inoltre infiniti segmenti maggiori del raggio del cerchio dato che possono fungere da raggio interno per la seconda corona circolare: finalmente, fissato anche questo raggio interno esiste una e una sola altezza per la seconda corona.
Che le corone siano concentriche o interne al cerchio dato è irrilevante (se non in quanto limita l'intervallo di raggi validi per la corona interna).
E' ovviamente possibile fare in modo che il raggio interno della corona esterna e il raggio esterno della corona interna siano uguali ottenendo una corona unica...
il panurgo
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
Principio di Relatività: $\mathbb{m} \not \to \mathbb{M} \, \Longleftrightarrow \, \mathbb{M} \not \to \mathbb{m}$
"Se la montagna non va a Maometto, Maometto NON va alla montagna"
Re: Cerchi e anelli
Suppongo che la parola “anello” stia ad indicare una “corona circolare”.
Dato un cerchio, di raggio r, il problema consiste quindi nel determinare due corone circolari, la prima di raggi $r_{1}$ e $r_{2}$ , con $r_{1}<r_{2}$ , la seconda di raggi $r_{3}$ e $r_{4}$, con $r_{3}<r_{4}$.
Al momento la posizione relativa nel piano della circonferenza e delle due corone non ci interessa; solo i cerchi di raggi $r_{1}$ e $r_{2}$ devono essere concentrici per aversi la corona circolare, e altrettanto dicasi per i cerchi di raggi $r_{3}$ e $r_{4}$. In pratica, per semplificare le figure, possiamo ritenere che le cinque circonferenze siano tutte concentriche in quanto, a problema risolto, i vati elementi possono essere traslati dove si vuole. Qundi anche le precisazioni di “anello interno” e “anello esterno” non sono rilevanti.
Fatte queste precisazioni, il problema richiede che la somma delle aree delle due corone circolari sia equivalente a quella del cerchio di raggio r.
Deve quindi essere $\pi\cdot r^{2}=\pi\left(r_{2}^{2}-r_{1}^{2}\right)+\pi\left(r_{4}^{2}-r_{3}^{2}\right)$ ovvero $r^{2}=r_{2}^{2}-r_{1}^{2}+r_{4}^{2}-r_{3}^{2}$ .
Da quest'ultima si può ricavare allora $r_{4}^{2}=r^{2}+r_{1}^{2}+r_{3}^{2}-r_{2}^{2}$.
Dai quattro segmenti di lunghezze rispettive $r, r_{1} , r_{2} , r_{3}$, con la semplice costruzione di tre triangoli rettangoli in successione si può costruire $r_{4}$.
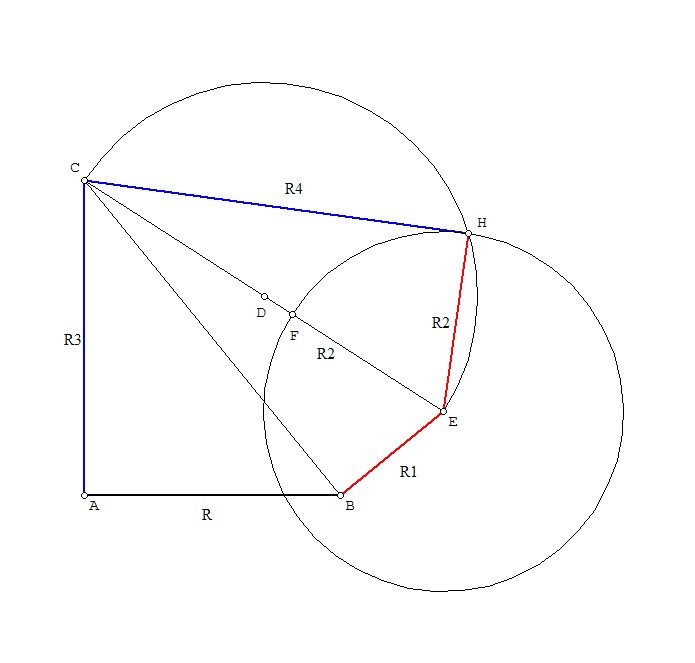
Si costruisce il triangolo ABC rettangolo in A con AB=r e $AC=r_{3}$. Allora $CB^{2}=r^{2}+r_{3}^{2}$.
Si costruisce il triangolo CBE rettangolo in B con $BE=r_{1}$. Allora $CE^{2}=CB^{2}+r_{1}^{2}=r^{2}+r_{3}^{2}+r_{1}^{2}$.
Si costruisce il triangolo CEH rettangolo in H con $EH=r_{2}$. Allora $CH^{2}=CE^{2}-r_{2}^{2}=r^{2}+r_{3}^{2}+r_{1}^{2}-r_{2}^{2}$.
Quindi CH è il raggio $r_{4}$ cercato.
Una volta ottenuti i cinque raggi si possono costruire, a piacere, il cercho e i due anelli.
Partendo dalla costruzione precedente ho costruito la seguente figura
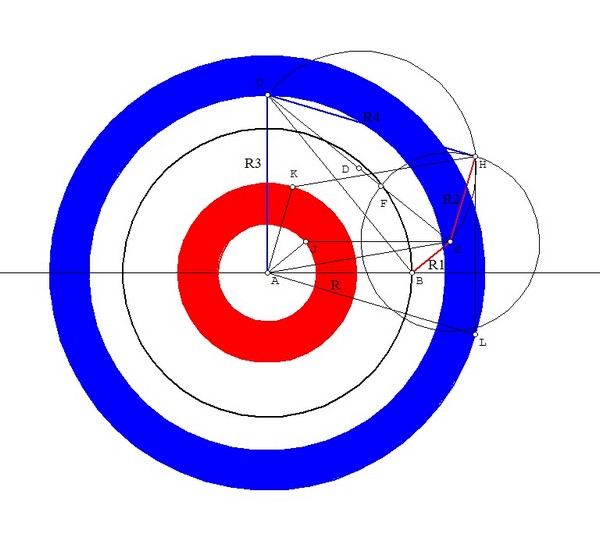
riportando a partire da A i raggi $r_{1}$ $r_{2}$ e $r_{4}$ e tracciando i cerchi.
La somma delle superfici delle corone circolari rossa e blu equivale alla suprficie del cerchio intermedio.
Non è neanche detto che gli “anelli” debbano essere delle corone circolari.
Costruendo i raggi con la tecnica precedente si può tracciare la figura seguente
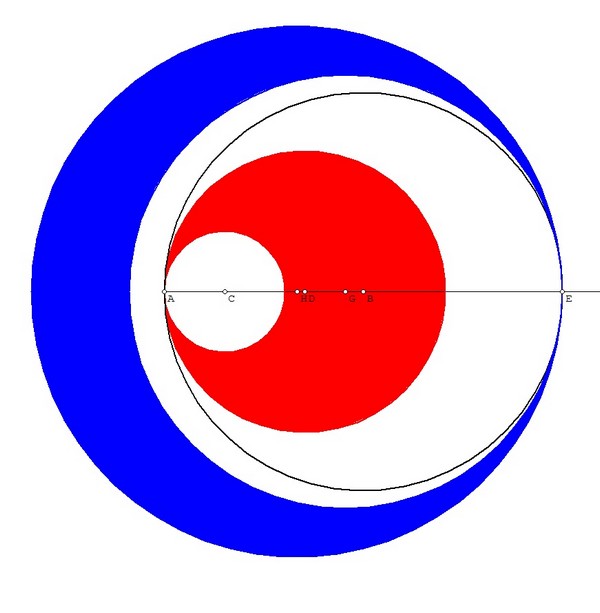
Anche in questo caso la somma delle superfici della zona rossa e di quella blu equivale alla superfice del cerchio intermedio.
P.S. Per fare le figure ho usato Wingeom col quale mi trovo più a mio agio. E' tuttavia chiaro che le medesime costruzioni si pssono ripetere in Geogebra.
Inoltre non è proprio necessario effettuare la costruzione preliminare dei raggi. Con programmi come Geogebra (o Wingeom) il raggio $r_{4}$ si può calcolare direttamente dalla formula a partire da $r, r_{1} , r_{2} , r_{3}$.
Spero di essere stato chiaro e di non aver commesso errori.
Dato un cerchio, di raggio r, il problema consiste quindi nel determinare due corone circolari, la prima di raggi $r_{1}$ e $r_{2}$ , con $r_{1}<r_{2}$ , la seconda di raggi $r_{3}$ e $r_{4}$, con $r_{3}<r_{4}$.
Al momento la posizione relativa nel piano della circonferenza e delle due corone non ci interessa; solo i cerchi di raggi $r_{1}$ e $r_{2}$ devono essere concentrici per aversi la corona circolare, e altrettanto dicasi per i cerchi di raggi $r_{3}$ e $r_{4}$. In pratica, per semplificare le figure, possiamo ritenere che le cinque circonferenze siano tutte concentriche in quanto, a problema risolto, i vati elementi possono essere traslati dove si vuole. Qundi anche le precisazioni di “anello interno” e “anello esterno” non sono rilevanti.
Fatte queste precisazioni, il problema richiede che la somma delle aree delle due corone circolari sia equivalente a quella del cerchio di raggio r.
Deve quindi essere $\pi\cdot r^{2}=\pi\left(r_{2}^{2}-r_{1}^{2}\right)+\pi\left(r_{4}^{2}-r_{3}^{2}\right)$ ovvero $r^{2}=r_{2}^{2}-r_{1}^{2}+r_{4}^{2}-r_{3}^{2}$ .
Da quest'ultima si può ricavare allora $r_{4}^{2}=r^{2}+r_{1}^{2}+r_{3}^{2}-r_{2}^{2}$.
Dai quattro segmenti di lunghezze rispettive $r, r_{1} , r_{2} , r_{3}$, con la semplice costruzione di tre triangoli rettangoli in successione si può costruire $r_{4}$.

Si costruisce il triangolo ABC rettangolo in A con AB=r e $AC=r_{3}$. Allora $CB^{2}=r^{2}+r_{3}^{2}$.
Si costruisce il triangolo CBE rettangolo in B con $BE=r_{1}$. Allora $CE^{2}=CB^{2}+r_{1}^{2}=r^{2}+r_{3}^{2}+r_{1}^{2}$.
Si costruisce il triangolo CEH rettangolo in H con $EH=r_{2}$. Allora $CH^{2}=CE^{2}-r_{2}^{2}=r^{2}+r_{3}^{2}+r_{1}^{2}-r_{2}^{2}$.
Quindi CH è il raggio $r_{4}$ cercato.
Una volta ottenuti i cinque raggi si possono costruire, a piacere, il cercho e i due anelli.
Partendo dalla costruzione precedente ho costruito la seguente figura

riportando a partire da A i raggi $r_{1}$ $r_{2}$ e $r_{4}$ e tracciando i cerchi.
La somma delle superfici delle corone circolari rossa e blu equivale alla suprficie del cerchio intermedio.
Non è neanche detto che gli “anelli” debbano essere delle corone circolari.
Costruendo i raggi con la tecnica precedente si può tracciare la figura seguente

Anche in questo caso la somma delle superfici della zona rossa e di quella blu equivale alla superfice del cerchio intermedio.
P.S. Per fare le figure ho usato Wingeom col quale mi trovo più a mio agio. E' tuttavia chiaro che le medesime costruzioni si pssono ripetere in Geogebra.
Inoltre non è proprio necessario effettuare la costruzione preliminare dei raggi. Con programmi come Geogebra (o Wingeom) il raggio $r_{4}$ si può calcolare direttamente dalla formula a partire da $r, r_{1} , r_{2} , r_{3}$.
Spero di essere stato chiaro e di non aver commesso errori.
Vittorio
Re: Cerchi e anelli
Bravo Vittorio, devo dire che hai colto in pieno la natura del problema (nonostante il mio uso enigmatico della terminologia)
La tua soluzione mi sembra ottima.
La tua soluzione mi sembra ottima.
[Sergio] / $17$




